二維陣列有很多用途，如果每一個格子的值是 0 或 1 的話，我們稱之為 0-1 矩陣。0-1 矩陣可以表達很多東西，比方說它可以是一個黑白影像、或者是一個運算用的遮罩、或者還可以拿來表示一個圖 (Graph) 的鄰接矩陣。

如果我們把一個 0-1 矩陣的內容想像成一張地圖上，哪些地方是土地、哪些地方是河流。對——比方說上面這張從 Inkarnate 製作的 RPG 地圖。（不得不說，這製作地圖的網站真的超強欸XD）

我們今天來看看在這個矩陣內找出一塊最大的長方形或正方形空地蓋房子的題目吧！

Example 9: Leetcode 221 - Maximal Square

題目連結

https://leetcode.com/problems/maximal-square/

題目敘述

給你一個 0-1 矩陣，請找出最大的正方形子矩陣使得裡面都是 1。

解題思考

我們定義 dp(i, j) 表示以 (i, j) 這格為右下角的時候，「全部都是 1 的正方形之最大邊長」。顯然根據這個定義，matrix[i][j] 是 "0" 的時候，無論如何都不能有正方形。因此在這個情形下 dp(i, j) = 0。那麼當 matrix[i][j] 是 "1" 的時候呢？我們注意到：假設答案是 k，那麼它的上方、左上方、左方都能夠畫出一個邊長是 k-1 的正方形！（因為只是少了一排而已啊）

反之，如果 (i, j) 的上方、左上方、左方三個格子的數值最小值為 x，那麼以 (i, j) 為右下角的正方形邊長不得超過 x+1（那也只能是 x+1 了。）
因此我們得到一個優雅的遞迴式：dp(i, j) = min(dp(i-1, j), dp(i, j-1), dp(i-1, j-1)) + 1。寫成 python 可以毫無壓力寫成一行呢！因為有三個數值要取最小值，用 C++ 反而沒那麼好寫呢。

參考程式碼(Python3)

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        arr = [list(map(int, row)) for row in matrix]
        for i in range(1, len(arr)):
            for j in range(1, len(arr[i])):
                arr[i][j] = min(arr[i-1][j], arr[i][j-1], arr[i-1][j-1]) + 1 if arr[i][j] == 1 else 0
        return max([max(row) for row in arr], default=0) ** 2

如果傳入空陣列到 max 函數的話，會有 Error，在 3.4+ 版指定預設值的話可以避免產生錯誤唷～

Example 10: Leetcode 85 - Maximal Rectangle

題目連結

https://leetcode.com/problems/maximal-rectangle/

題目敘述

給你一個 0-1 矩陣，請找出最大的長方形子矩陣使得裡面都是 1。

解題思考

這題有兩種線性時間（與矩陣總格子數成正比的時間）的作法。第一種是利用堆疊，對於每一列都紀錄著該位置往上看的高度為何（往上看最遠可以看幾格）。然後利用 https://leetcode.com/problems/largest-rectangle-in-histogram/ 這題的作法在線性時間內找出以某一列為底，最大的矩形面積為何。（一點都不違和！）

第二種方法是我覺得比較帶有證明色彩的。首先我們可以透過觀察，得出「面積最大的矩形，必須要碰觸到上、左、右邊界至少一個格子」。各位朋友想必有注意到——我故意不考慮下界的格子。然後呢，我們可以定義 dp(r, c) 表示為：從 (r, c) 這格往上看，如果我們考慮的矩形、向上延伸時碰觸到了 (Up(r, c), c) 這個格子、並且以第 r 列作為底邊的時候，最大的面積為何？這裡的 Up(r, c) 是指從 (r, c) 這格往上看，直直看上去撞到的第一個障礙物的列數。這個 Up 表格我們可以先順手處理起來。

經過一陣推敲，我們可以發現以 (Up(r, c), c) 這格作為上界、並以第 r 列作為下界的矩形，面積最大者，必須是這中間每一格看左、看右，能看遠就盡量看遠：也就是說我們可以在動態規劃時一起維護 Left(r, c) 和 Right(r, c) 之值。

最後，我們只要證明，答案一定會被我們 cover 在某一個 dp(r, c) 裡頭即可：根據觀察，最佳解一定觸碰到上、左、右三個邊界，假設它觸碰到了 (r', c') 這個上界的格子。那麼往下找，這個矩形一定會被紀錄在同一列稍微下方的 dp 表格內。因此 dp 表格的最大值就是答案啦！

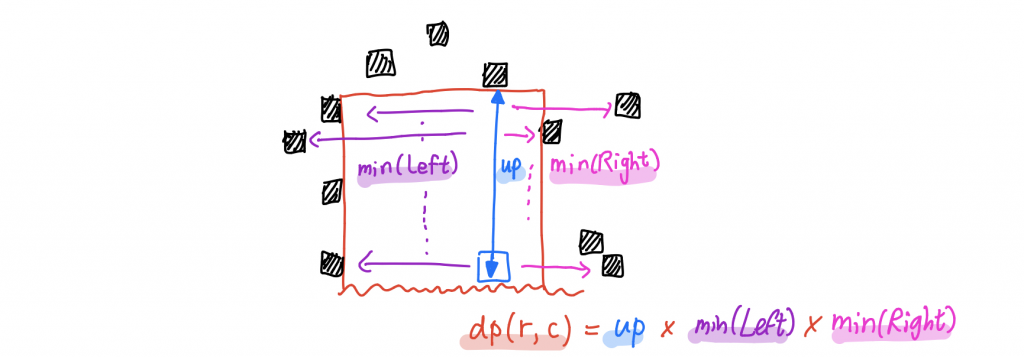
▲這是一個帶有證明色彩的有色彩的證明。

參考程式碼(Python3)

雖然效率跟程式碼長度都比堆疊差，但我還滿喜歡這個解法的哈哈哈。

from itertools import accumulate

class Solution:
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        if len(matrix) == 0:
            return 0
        arr = [list(map(int, x)) for x in matrix]
        n = len(matrix[0])
        up, left, right = [0] * n, [0] * n, [0] * n
        ans = 0
        for row in arr:
            row_left = list(accumulate(row, lambda val, x: (val + x) * x))
            row_right = list(accumulate(row[::-1], lambda val, x: (val + x) * x))[::-1]
            up = [(val + x) * x for val, x in zip(up, row)]
            left = [min(x, y) if u > 1 else y for x, y, u in zip(left, row_left, up)]
            right = [min(x, y) if u > 1 else y for x, y, u in zip(right, row_right, up)]
            for u, l, r in zip(up, left, right):
                ans = max(ans, u * (l + r - 1))
        return ans

後話

以前好像出過三角形格子點版本、還有六邊形格子點版本......