這週歸納了兩個演算法技巧,於Matters介紹
我的Matters:前端野人
說明: 計算符合k的子組串數量
Example 1:
Input:nums = [1,1,1], k = 2
Output: 2
思維:
這題我一開始想說可以應用上禮拜的DP來運算,但反而卡住了,我從中得到一個經驗,解題目不要預設思維。
這題有個思維很簡單,就是每個元素都找出所有組合是否符合k,簡單好懂,能AC但速度上是很慢的。
var subarraySum = function(nums, k) {
let sum = k
let answer = 0
for(let i = 0; i < nums.length ; i ++){
let sum = 0
for(let j = i ; j < nums.length;j++){
sum += nums[j]
if(sum == k) answer +=1
}
}
return answer
};
這題最佳解是用hashmap,hashmap的解法是一直累加sum,然後在判斷 sum -k的值有沒有在hashmap裡面,有的話就累計。
Answer:
var subarraySum = function(nums, k) {
let sum = 0
let hash = new Map()
hash.set(0,1)
let answer = 0
for(let i = 0 ; i < nums.length ; i++){
sum += nums[i]
if(hash.has(sum - k)){
answer += hash.get(sum - k)
}
hash.set(sum, (hash.get(sum) || 0) + 1)
}
return answer
};
說明: 程式語言的位元運算子,可參考Bitwise and (or &) of a range - GeeksforGeeks
思維: 題目意思就是得到兩個之間所有數字得二進位的共同位數,
| 十進位 | 二進位 |
|---|---|
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
而程式語言已經有判斷的運算值,只要用&就可以找到了,所以這題問題就會變成是怎麼重複做a & b。
我一開始是想試一下以前所學的技巧recursion,所以這樣寫:
var rangeBitwiseAnd = function(m, n) {
let nums = []
let answer = 0
let bitwise = (a,b) =>{
if(b > n) return
answer = a & b
bitwise(answer, b + 1)
}
if (m==n) return m & n
bitwise(m,m+1)
return answer
};
這樣寫觀念是正確的,但有個致命缺點就是如果跑太多次會出現Maximum call stack size exceeded的錯誤,所以這是不可行的做法。
最佳解是使用>>運算,>>會將數字的二進位的最右邊拿掉,如下面所示,這樣就可以找到相似值,但因為是shift,所以結束時要用 <<補0,count是紀錄要補幾個0。
| 十進位 | 二進位 |
|---|---|
| 5 >>=1 | 10 |
| 7 >>=1 | 11 |
| 十進位 | 二進位 |
|---|---|
| 2 >>=1 | 1 |
| 3 >>=1 | 1 |
符合後因為這個運算做了兩次,所以答案要補兩個
0,100 = 4
var rangeBitwiseAnd = function(m, n) {
let count = 0;
while (m != n) {
count++;
m >>= 1;
n >>= 1;
}
return m << count;
};
說明: 實作 LRU Cache。
Example:
LRUCache cache = new LRUCache( 2 /* capacity */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // returns 1
cache.put(3, 3); // evicts key 2
cache.get(2); // returns -1 (not found)
cache.put(4, 4); // evicts key 1
cache.get(1); // returns -1 (not found)
cache.get(3); // returns 3
cache.get(4); // returns 4
解析:
跟js的Map很像,但存取機制卻是跟pop、push一樣,而且有容量限制。所以還要在function get(key),顛倒存放順序,把後面移到前面,因為當超過容量時,可以使用Map.keys()取得第一個key值,因為Map沒有pop的操作,所以要用這種方式,剩下的就可以照題意實作。
Answer:
var LRUCache = function(capacity) {
this.capacity =capacity
this.hash = new Map()
};
/**
* @param {number} key
* @return {number}
*/
LRUCache.prototype.get = function(key) {
if(!this.hash.get(key)){
return -1
}
const value = this.hash.get(key);
this.hash.delete(key);
this.hash.set(key, value);
return value;
};
/**
* @param {number} key
* @param {number} value
* @return {void}
*/
LRUCache.prototype.put = function(key, value) {
if(this.hash.has(key)) this.hash.delete(key)
this.hash.set(key,value)
// 超過就把第一個value刪掉。
if(this.hash.size > this.capacity){
const ind =this.hash.keys().next().value
this.hash.delete(ind)
}
};
說明:以陣列中的元素作為移動距離,依照元素加總向右位移,判斷能否指向最後一個元素。
Example 1:
Input: nums = [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.
Example 2:
Input: nums = [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it
思維:
這題有一個最基本的解法是用Backtracking,因為是使用recursion,所以數組太多時會Time Limit Exceeded,但是觀念來說是有助於理解這題的解法。
題目所述,每個元素代表的是maximum jump length,所以最少為1,而Backtracking則是判斷每個可能移動的距離來確認要選哪個距離量並往下探訪直到不能走為止,所以這樣走確實會因為數組長度太大而不能AC。
var canJump = function(nums) {
const canJumpFormPosition = (position, nums) => {
if(position == nums.length -1 ){
return true
}
const furthestJump = Math.min( position + nums[position] , nums.length -1)
for(let nextPosition = furthestJump ; nextPosition > position ; nextPosition --){
if(canJumpFormPosition(nextPosition ,nums)) return true
}
return false
}
return canJumpFormPosition(0,nums)
};
但是Backtracking仍然是正確的思路,所以如果要AC就要讓Backtracking不做沒有必要的走訪。為了減少不必要的走訪,就要暫存確定不能走的索引值,所以要用memo來判斷是否能用。首先先記錄所有元素是Unknown,只要是能繼續走訪的元素就是Good。如果不是那就是Bad,雖然能AC但這是最差的解法,最後還有最佳優化解。
var canJump = function(nums) {
const type ={
Good:"G",
Bad :"B",
Unknown:"U",
}
let memo = new Array(nums.length)
for(let i = 0 ; i < nums.length ; i++){
memo[i] = type.Unknown
}
memo[nums.length - 1] = type.Good
const canJumpFormPosition = (position, nums) => {
if(memo[position] !== type.Unknown){
return memo[position] == type.Good ? true : false;
}
const furthestJump = Math.min( position + nums[position] , nums.length -1)
for(let nextPosition = furthestJump ; nextPosition > position ; nextPosition --){
if(canJumpFormPosition(nextPosition ,nums)){
memo[position] = type.Good
return true
}
}
memo[position] = type.Bad;
return false
}
return canJumpFormPosition(0,nums)
};
最佳解為Greedy,我們可以觀察到如果元素不是0的話通常是能到終點的,而Greedy就直接判斷,i + nums[i]是否剛好或是大於nums.length,因為能到達終點的話距離一定會大於nums.length或是剛好等於nums.length,Greedy從最後一個元素開始找。只要能超過那該元素的索引值就往回找而且到達該索引的距離一定大於或等於到該索引的長度,如果是能過的話那最後一定會找到起點。這樣確實快很多,但思維就跟Backtracking截然不同,Backtracking是照題意思考,而Greedy則是歸納出最簡單解的思維而得出。
var canJump = function(nums) {
let lastInd = nums.length - 1
for(let i = lastInd ; i >= 0 ; i--){
if(i + nums[i] >= lastInd){
lastInd = i
}
}
return lastInd == 0
};
說明:經典的最長公子序列。
Example 1:
Input: text1 = "abcde", text2 = "ace"
Output: 3
Explanation: The longest common subsequence is "ace" and its length is 3.
Example 2:
Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.
Example 3:
Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.
思維:一開始我是想用hashmap紀錄所有相同的字母數量然後累計最小次數,但有一個問題是題目有補充:(eg, "ace" is a subsequence of "abcde" while "aec" is not)如果順序不對的話就不算,所以這想法就只能放棄。
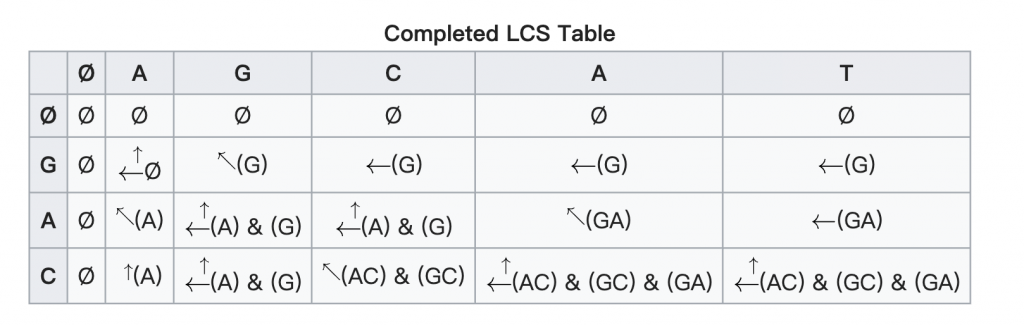
所以最後還是要回來看LCS的原理,下圖是LCS的演算法圖示,LCS使用DP做出兩個字串比對的二維陣列,但長寬會比兩個字串的長度還多1,原因是在於DP會用dp[i-1]累計,所以開頭要有初始值,迴圈開始判斷有沒有相符合的字母,但下面的走訪圖會發現一個問題,好像走訪並沒有看順序而是累計一樣的次數而已,其實LCS是找出可能的子序列最後在找出最長的序列,下面第二張圖可以看到真正走訪的結果。
| 順序 | 走訪 | 比對字串 | 判斷 |
|---|---|---|---|
| 1 | dp[1,1] | [A,G] | Max(0,0) |
| 2 | dp[1,2] | [A,A] | 1 |
| 3 | dp[1,3] | [A,C] | Max(0,1) |
| 4 | dp[2,1] | [G,G] | 1 |
| 5 | dp[2,2] | [G,A] | Max(1,1) |
| 6 | dp[2,3] | [G,C] | Max(1,1) |
| 7 | dp[3,1] | [C,G] | Max(1,0) |
| 8 | dp[3,2] | [C,A] | Max(1,1) |
| 9 | dp[3,3] | [C,C] | 2 |
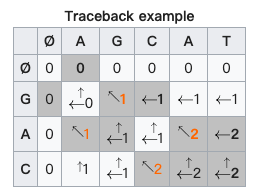
這張圖才是LCS真正做的事,LCS找出了A、G、AC、GC、GA,這幾個子序列,其中最長的子序列為2。所以DP是用來紀錄可能的子序列長度
var longestCommonSubsequence = function(text1, text2) {
const dp = [];
let m = text1.length;
let n = text2.length;
for (let i = 0; i <= m; i++) {
dp[i] = new Array(n + 1).fill(0);
}
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (text1.charAt(i - 1) != text2.charAt(j - 1)) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
else {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
}
}
return dp[m][n];
};
說明在二維陣列中找出1的範圍所圍成最大正方形。
Example:
Input:
1 0 1 0 0
1 0 `1 1` 1
1 1 `1 1` 1
1 0 0 1 0
Output: 4
思維:
首先要先找出,二維陣列的長寬(m,n)
let rows = matrix.length
let cols = row !== 0 ? 0 : matrix[0]
再來是設計dp,max為正方形的長寬,最小的正方形為一個1,所以在設計dp時就需要找出max,因為dp都是從dp[1][1]開始所以要先設定好最外圍的值。
for(let i = 0 ; i < rows ; i++){
dp[i] = new Array(cols).fill(0)
}
for (let i = 0; i < rows; i++) {
dp[i][0] = Number(matrix[i][0]);
max = Math.max(max, dp[i][0]);
}
for (let j = 0; j < cols; j++) {
dp[0][j] = Number(matrix[0][j]);
max = Math.max(max, dp[0][j]);
}
[ [ 1, 0, 1, 0, 0 ],
[ 1, 0, 0, 0, 0 ],
[ 1, 0, 0, 0, 0 ],
[ 1, 0, 0, 0, 0 ] ]
找出,matrix最外圍的值後就可以開始從dp[1][1]運算,每次找到1就要判斷他是否為正方形,所以就要找1的左上角,上面,左邊是否為1,假設有一角是0那dp紀錄當下的元素1,提供下一個元素判斷。
for (let i = 1; i < rows; i++) {
for (let j = 1; j < cols; j++) {
if (matrix[i][j] === 1) {
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1;
max = Math.max(max, dp[i][j]);
}
}
}
照判斷走完,最後會得到結果:
[ [ 1, 0, 1, 0, 0 ],
[ 1, 0, 1, 1, 1 ],
[ 1, 1, 1, 2, 2 ],
[ 1, 0, 0, 1, 0 ] ]
dp的思維是把dp[1][1]當作是正方形的右下角,這樣就可以用dp的特性找出其他三角是否都有1,假設右下角為1再找min(其他三角)為多少,只要其他三角都一樣長度,那自然就能在右下角得到正方形的長寬。
說明:找出二元樹中最大的子樹。
思維:先想哪個root,left,right加起來最大,所以會先得出一個規則:
sum = node.left + node.right + node.val
但又要思考,每個root又可能是其他node的left或是right,所以要想如果是root節點的left跟right是不是就是這節點之下最大的和。
這樣就能套用到每個node,以example 2當例子。
Example 1:
Input: [1,2,3]
1
/ \
2 3
Output: 6
Example 2:
Input: [-10,9,20,null,null,15,7]
-10
/ \
9 20
/ \
15 7
Output: 42
| node | left | right | sum |
|---|---|---|---|
| -10 | 9 | 42 | 41 |
| 9 | null | null | 9 |
| 20 | 15 | 7 | 42 |
而我們只抓max(sum)所以答案是42,所以dfs就是找當下節點下這棵樹最大值為何。
Answer:
var maxPathSum = function(root) {
let sum = root.val;
const dfs = (node) => {
if (!node) return 0;
const left = Math.max(dfs(node.left), 0),
right = Math.max(dfs(node.right), 0);
sum = Math.max(left + right + node.val, sum);
return Math.max(left, right) + node.val;
}
dfs(root);
return sum;
};
好不容易做好第一篇系列文,但沒想到後面這麼硬,但也因此學到比較深入的程式思維
原本計畫這系列寫完就開始做side project,而剛好今天 @海綿寶寶 想找人做 open source 我就順勢接下去玩了。
