記錄學習內容。看網路上大大們的文章和影片，做些紀錄。
還不了解，內容可能有錯誤。

Longest Increasing Subsequence (最長遞增子序列)

這個問題就是
如果有一個數列是

1 , 2 , 3 , 4, 5 , 6, 7

那這個數列的Longest Increasing Subsequence 就是

1 , 2 , 3 , 4, 5 , 6, 7
是7個

如果一個數列是

1 , 2 , 3 , 4, 5 , 6, 7,7,7

那這個數列的Longest Increasing Subsequence 就是

1 , 2 , 3 , 4, 5 , 6, 7
還是7個，因為是Increasing (遞增)

如果是求Longest Non-Decreasing Subsequence

那就是

1 , 2 , 3 , 4, 5 , 6, 7,7,7
是9個 ，因為Non-Decreasing(不減少)

有很多種解法 ， 先從感覺比較懂得開始看:

１　Dynamic Programming (動態規劃)解法:

Find The Longest Increasing Subsequence - Dynamic Programming Fundamentals
https://www.youtube.com/watch?v=fV-TF4OvZpk&ab_channel=BackToBackSWE

教學裡的例子

1、 3 、 4、 5、 2、 2、 2、 2
找這個數列的Longest Non-Decreasing Subsequence 

先多準備一個陣列 ，紀錄東西 。
1  3   4   5   造著順序 ，所以1 2 3 4 代表這4個數字的Longest Non-Decreasing Subsequence 。

到數列裡的2 的時候 ， 因為小於3 ，所以只接1  ，Longest Non-Decreasing Subsequence 會是 1+1 = 2 。

剩下 數列裡的2 就會3 4  5 。

最後多準備的這個陣列 裡面，數字最大的那個數 。
就代表這個數列 ，  最長 Non-Decreasing 的 數列 長度 。

來看程式:
300. Longest Increasing Subsequence
https://leetcode.com/problems/longest-increasing-subsequence/solution/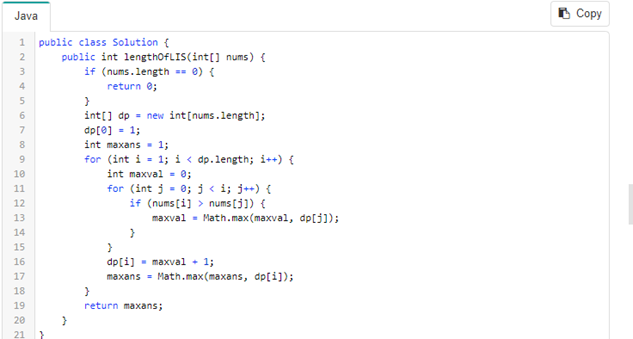

一

第一層迴圈 ， 就是 走訪數列
第二層迴圈 ， 就是 i 索引之前的數字
像是現在走到 [2,3,4,5] 裡的 4  ， i是 2索引 。J 是 0索引 、1索引 。
4 會先跟 2 比大小 ，4比較大 ， 所以
Math.nax(4當前LIS , 2的LIS ) 。 決定要不要更新4 的LIS 。

最後結果--- > dp[]裡 的每個數字 代表 那個數字的Longest Increasing Subsequence ，
所以 dp[]裡最大的那個數字 ，會是答案

這邊的寫法是 ，每一個數字算出Longest Increasing Subsequence 後 ，就去更新最大值 。
maxans 最後就會是 dp[]裡最大的那個數字 。 (最大數字可能有很多一樣的，因為Longest Increasing Subsequence 可能有很多個)

二

if (nums[i] > nums[j]) {
    maxval = Math.max(maxval, dp[j]);
}

改成

if (nums[i] >= nums[j]) {
    maxval = Math.max(maxval, dp[j]);
}

就變成Longest Non-Decreasing Subsequence 了

時間複雜度 :

time -- > 因為1+2+3+….n-1 ，會有 n * n 出現 (兩層迴圈)
space -- > 因為要多準備一個陣列 n size

2 Dynamic Programming with Binary Search

input: [0, 8, 4, 12, 2]
dp: [0]
dp: [0, 8]
dp: [0, 4]
dp: [0, 4, 12]
dp: [0 , 2, 12]

這個方法也是走訪每一個數字 ，
先準備一個陣列dp 。
一開始是0 ，就放0 。
接著 Binary Search  8  ，因為dp裡只有0 ，8大於0 ，所以繼續放8 。

接著 Binary Search   4 ，因為dp介於0-8之間，所以 不是變成0 4 8 ，而是變成0 4 ，因為4<8 不能0 4 8 ，
所以只能取代 8。

接著 Binary Search   12 ，因為12 最大 ， 所以放到最後面 0 4 12 。
接著 Binary Search   2 ，2介於0-4 ，取代4 ，變成0、2、12 。

所以最後的陣列長度 ，就是答案 。

leetcode範例裡的解答看不懂 ，看這篇文章:

[LeetCode] 300. Longest Increasing Subsequence 最长递增子序列
https://www.cnblogs.com/grandyang/p/4938187.html

解法2 :

最小放dp[0] ，最大放dp的最後面 。
其他的用Binary Search ，找到 第一個 不小於(大於等於) 這個元素的index，
蓋掉他

像是

input: [0, 8, 4, 12, 2]

dp: [0]

dp: [0, 8]:

    第一次
    left =0 ，right = 2
    mid = 0 +  2/2  = 1
    if ( 8 < 4) left = mid+ 1
    else right = mid       //( right = 1)

    第二次
    left =0 ，right = 1
    mid = 0 +  1/2  = 0
    if ( 0< 4) left = mid+ 1  // left = 1
    else right = mid  

    之後
    Ends [1 ]  = 4

所以變成[0,4]

複雜度

時間複雜度:

因為 迴圈 長度 n ，每一輪Binary Search 都logn 。
時間複雜度 n * logn 

3 Brute Force

覺得遞迴的方法最難懂 。
平常的遞迴 都是5 4 3 2 1 ，從n到1 。
但是這個演算法的遞迴是 從0 到 n ，12345。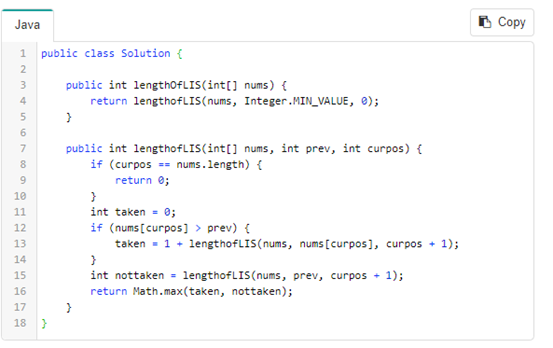

Nums 是 數字陣列 。
Curpos  指的是current position ，現在在哪個陣列索引 。
Prev 指的是 上一個要比較的值(value) 。

如果數列是 1 2 3 4 5

現在在2 ， 2 可以選擇 ，2可以不選擇 。
選擇-- >  1 (長度+1)  + 下一個遞迴( 比較的數字從1移動2 , current position+1)
不選擇 --- >下一個遞迴( 比較的數字還是1, current position+1)

教學來源:
花花酱 LeetCode 300. Longest Increasing Subsequence (Dynamic Programming O(n^2)) - 刷题找工作 EP48
https://www.youtube.com/watch?v=7DKFpWnaxLI&t=974s&ab_channel=HuaHua

複雜度

時間複雜度

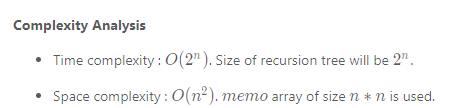
不太懂 ，因為每個數字都要選或不選 ，所以2的n次方 。
2.1.4 Recurrence Relation T(n)=2 T(n-1)+1 #4
https://www.youtube.com/watch?v=JvcqtZk2mng&list=PLDN4rrl48XKpZkf03iYFl-O29szjTrs_O&index=22&ab_channel=AbdulBari

空間複雜度:

不懂。可能是因為 遞迴高度 是 n (陣列個數) ，
每一個遞迴都有一個int[] nums 陣列 ，陣列個數n 。
所以n*n 。

4 Recursion with Memoization

時間複雜度

因為　存了ｎ＊ｎ個東西　，所以算ｎ＊ｎ次

空間複雜度:

因為　存了ｎ＊ｎ個東西