在實作之前我們先來認識Heap

堆積 (Heap)，是一種特殊的完全(complete)二元樹，也就是除了最後一層樹葉，每一層都是長滿的。

而今天要建構的Min-Heap多了一個特點，就是了父結點都要小於或等於子結點; 相反的，Max-Heap則是父結點都要大於或等於子結點。

我將要用一個沒有被排列過的陣列，採用in-place的方式，來建構出一個符合min-Heap性質的陣列，我們會實作兩個函式，分別是heapifyDown() 和 heapifyUp()，它們都可以用來建構Min-Heap（build Heap），此外我們還需要其他兩個函式分別是insert()以及remove()。

實作兩個函式前我們要先知道如何推得heap的父結點t以及子結點的索引（index）以及它們之間的關係式。我們先以下圖為例

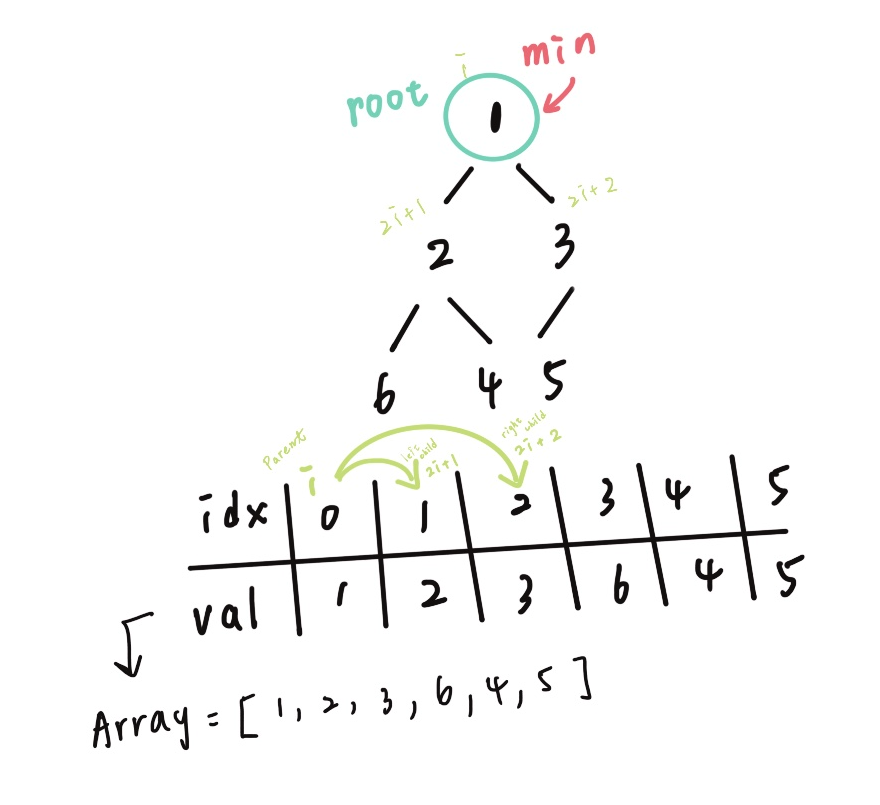
我可以觀察出，假設現在在的節點 index = i

則 leftChild = 2i+1 ; rightChild = 2i+2，而 parent = (i-1) / 2 取 floor

利用這種簡單的計算方式，我們就可以很輕易地取得parent和child（以O(1)的時間複雜度）

接下來我們就來看如何在heap中插入節點→ insert()

假設我們今天要把上方的heap加入0，我們該如何操作？

1. 我們會把0加在最後面(last node)，也就是3的rightChild，但我們知道加進去的元素不可能一定洽在正確的位置，所以我們需要將它作向上調整的動作（ heapifyUp() ），這個方法會不斷的將插入的節點與其父節點比較，若有需要則會swap()

2. 以這張圖來說：因為 3 > 0 所以需要交換，以次類推如下圖，最後可以獲得最右邊的min heap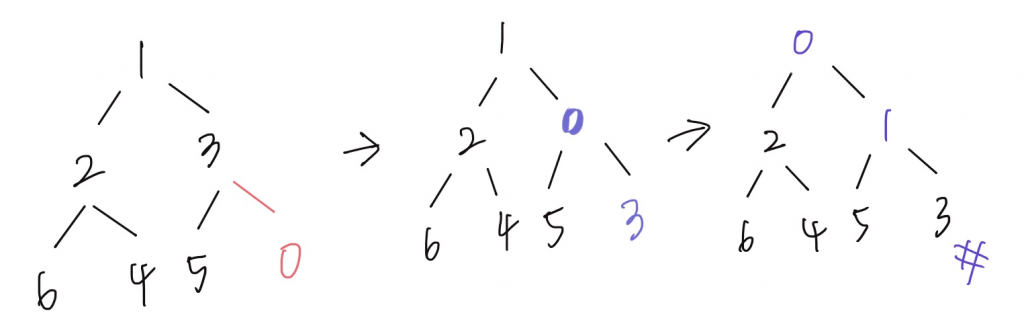
   

3. 若用陣列的幾角度來看 ，則是利用push的方式加到陣列最後面 array = [ 1, 2, 3, 6, 4, 5, 0]，0的index為6，要比較的parent就是 floor((6-1)/2) = 2 （array[2] = 3），我們直接在array做swap的動作。以下先來寫swap()

const swap = (i, j, heap) => {
		const tmp = heap[j];
		heap[j] = heap[i];
		heap[i] = tmp;
	}

1. 依照上面重複的邏輯就是heapifyUp()

不過在這裡暫停一下，先來寫remove()，這裡的remove我們要做的是：移除heap的最小值（以後一定會碰到我們用heap的資料結構來移除最大或最小值 → peek() 其實就是回傳array[0] ）

操作方式如下：

1. 我們直接把array的array[0]和array的最後一個元素（array[array.length-1]）做swap，然後直接用pop()的方式移除陣列最後一個元素，而後再對heap做調整（heapifyDown()：其實就是拿array[0]開始往後調整的感覺），換作是圖就會如下。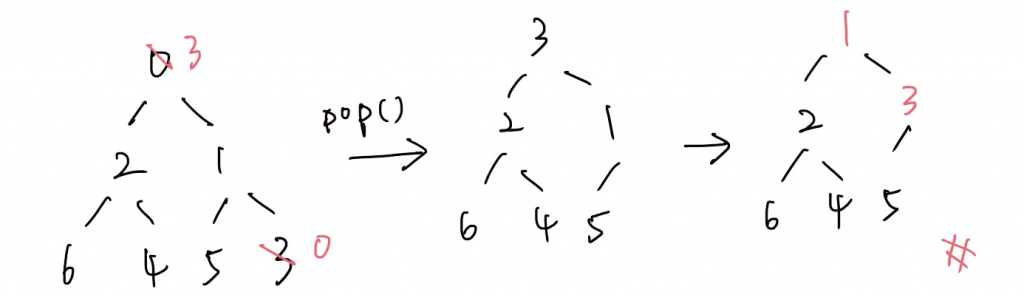
   

2. 注意heapifyDown是要把左右兒子小的往上面交換

3. 若用陣列的幾角度來看 ，則是先swap() → array = [ 3, 2, 1, 6, 4, 5, 0 ] → pop() → array = [ 3, 2, 1, 6, 4, 5] → heapifyDown()

建構 Heap 使用heapifyDown，從最左邊的parent開始（較佳）-> 整體時間複雜度: O(N)
空間複雜度 : O(1) 不需額外的空間

說到這裡我們就直接來實作吧！

class MinHeap {
  constructor(array) {
    this.heap = this.buildHeap(array);
  }

  buildHeap(array) {
		// 採用heapifyDown, Time: O(n), space O(1)
		const firstIdx = Math.floor((array.length -2) / 2);
		for(let currentIdx = firstIdx; currentIdx >= 0; currentIdx --){
			this.heapifyDown(currentIdx, array.length, array);
		}
    return array;
  }

  heapifyDown(currentIdx, endIdx, heap) {
    let leftChildIdx = currentIdx*2+1;
		while(leftChildIdx<=endIdx){
			// 確認是否有右兒子
			const rightChildIdx = currentIdx*2 +2 <= endIdx ? currentIdx*2 +2 : -1;
			let swapIdx;
			// 找出較小的child
			if(rightChildIdx!==-1 && heap[rightChildIdx] < heap[leftChildIdx]){
				swapIdx = rightChildIdx;
			}else{
				swapIdx = leftChildIdx;
			}
			// 如果較小的child 小於 parent 則swap，且要繼續往"下"確認
			if(heap[swapIdx] < heap[currentIdx]){
				this.swap(currentIdx, swapIdx, heap);
				currentIdx =  swapIdx;
				leftChildIdx = currentIdx*2+1;
			}else{
				return;
			}
		}
  }

   heapifyUp(currentIdx, heap) {
    let parentIdx = Math.floor((currentIdx -1)/2);
		// 每次比較當下node和parent的值，如果比較小要和parent swap ，而後再繼續往"上"檢查
		while(currentIdx > 0 && heap[currentIdx] < heap[parentIdx]){
			this.swap(currentIdx, parentIdx, heap);
			currentIdx = parentIdx;
			parentIdx =  Math.floor((currentIdx -1)/2);
		}
  }

	// 傳回root O(1)
  peek() {
    return this.heap[0];
  }

 //把根移除 
	remove() {
		//把跟和最後一個元素交換後 再做heapifyDown調整
  	this.swap(0, this.heap.length -1, this.heap);
		const removeValue = this.heap.pop();
		this.heapifyDown(0, this.heap.length -1, this.heap);
		return removeValue;
  }


  insert(value) {
		// 加到最array後面
    this.heap.push(value);
		// 用heapifyUp 調整
		this.heapifyUp(this.heap.length - 1, this.heap);
  }
	
	swap(i, j, heap){
		const tmp = heap[j];
		heap[j] = heap[i];
		heap[i] = tmp;
	}
}

其實max-heap就是仿造上面的程式碼把一些大於小於做調整就可以了！別忘了自己coding一下喔！

明日題目預告：我們已經陸續用了不少的sort來解問題，明天開始就讓我們實作不同的經典排序方法來解同一道題目吧！之後也會用到heap的結構來解喔！ Sort an Array