Excel隨機機率產生技能組問題

機率 excel隨機機率產生技能組

ccx12462000 2021-01-25 18:25:10 ‧ 1358 瀏覽

分享至

我擁有六組技能，分別A/B/C/D/E/F
A:代表被動
B:代表技能1
C:代表技能2
D:代表技能3
E:代表技能4
F:代表絕招

我想要的設計是，一副牌有40張牌，1張牌可以隨機出現2種技能，
例:艾希:AC或艾希:DF

但我想要讓技能組合機率不一樣，比如我不希望一副牌擁有F的組合超過3個或擁有A的組合超過10個，F可以是0不出現，A最少要出現5個，以作為整副牌的平衡。

目前我可以隨機出技能組，但F跟A的出現遠遠超過預期，不知道如何去限制他們

微笑 iT邦研究生 5 級 ‧ 2021-01-29 09:30:40 檢舉

那就把40張牌內的前13筆拿出來
前5筆出現A+BCDE
6~10筆出現 ABCDE + BCDE
11~13筆出現 BCDEF + BCDE
14~40筆出現 BCDE + BCDE

將基礎資料設定為BCDE，A跟F特殊處理

至於前後資料如何不重複，參考上一個問題的解答即可

登入發表討論

直播研討會

{{ item.channelVendor }} {{ item.webinarstarted }} |

直播中

2 個回答

海綿寶寶

iT邦大神 1 級 ‧ 2021-01-25 20:44:29

產生 0-99 的亂數，其中
0-9 表示 A
10-19 表示 B
20-29 表示 C
完整對照表如下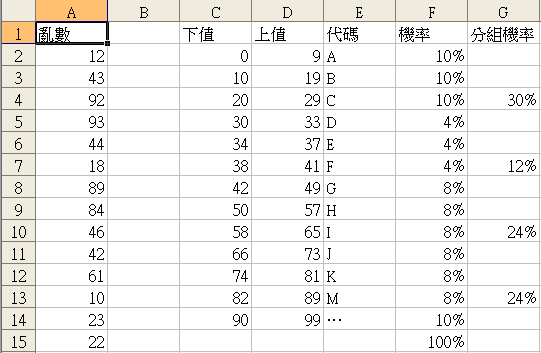

A1=INT(RAND()*100)

回應 8
分享
檢舉

看更多先前的回應...收起先前的回應...

ccx12462000 iT邦新手 5 級 ‧ 2021-01-25 21:36:00 檢舉

大大請問一下，我在做一個測試，一名英雄有6個技能分別為被動/Q/W/E/R/大招，我想實現的是一副卡牌裡面的卡，同時擁有2個技能，但卻是隨機，被動/Q/W/E/R/大招組合的機率有所不同，例如:不想讓大招在一副卡牌中出現3次以上，有先技能組可以常出現，那這樣的寫法可以實現嗎?

海綿寶寶 iT邦大神 1 級 ‧ 2021-01-26 09:09:56 檢舉

我看不懂你寫的
但我想應該可以

原則做法是
不要「全部用亂數產生再挑選符合條件的組合」
而是「先準備符合條件的組合，再用亂數去挑選」

你可以先想看看類似的題目
「發樸克牌給四個人，每人13張，52張牌不能重覆」
(你在發牌的時侯，從來不需要去檢查每張牌是否重覆對吧？)
或者
「不需要檢查彼此是否重覆，就產生一個彼此不重覆的四位數字」

ccx12462000 iT邦新手 5 級 ‧ 2021-01-26 11:05:14 檢舉

我改清楚一點說明

海綿寶寶 iT邦大神 1 級 ‧ 2021-01-26 12:33:53 檢舉

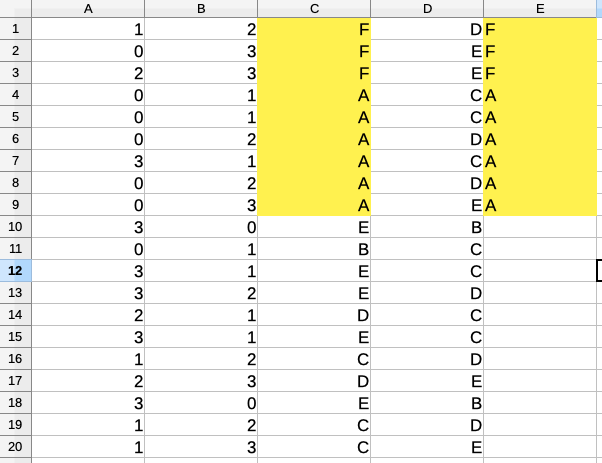
用亂數處理六分之四的規格
剩下的六分之二
用手動的方式處理
上圖為(Fx3, Ax5)的範例
要更多或更少的 A,F 都在 E 欄輸入即可

A1=INT(RAND()*4)
B1=MOD(A1+INT(RAND()*3)+1,4)
C1=IF(ISBLANK(E1),CHOOSE(A1+1,"B","C","D","E"),E1)
D1=CHOOSE(B1+1,"B","C","D","E")
E1=F(手動輸入)

如果連 E 欄的 A,F 值(數量)都要隨機產生
大概得寫一小段 VBA 了...

ccx12462000 iT邦新手 5 級 ‧ 2021-01-26 14:32:52 檢舉

謝謝老師，我來研究一下~

ccx12462000 iT邦新手 5 級 ‧ 2021-01-26 15:00:39 檢舉

都要隨機出現，我希望有可人一副牌裡面都沒有F，或只有1~3張，A是5~10張，隨機的，這樣每副牌才有不同之處

ccx12462000 iT邦新手 5 級 ‧ 2021-01-26 15:04:02 檢舉

老師你下方範例是人工去決定A與F的數量嗎?，那如果隨機就要換寫法是嗎?

海綿寶寶 iT邦大神 1 級 ‧ 2021-01-26 15:43:53 檢舉

改成這樣就連 A,F 都用亂數產生了
F 是 F1, 0..3
A 是 G1, 5..10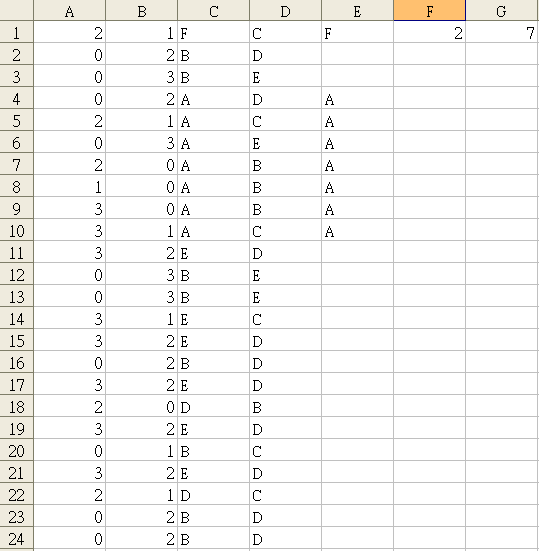

A1=INT(RAND()*4)
B1=MOD(A1+INT(RAND()*3)+1,4)
C1=IF(E1="",CHOOSE(A1+1,"B","C","D","E"),E1)
D1=CHOOSE(B1+1,"B","C","D","E")
E1..E3=IF(ROW()<=$F$1,"F","")
E4..E13=IF((ROW()-3)<=$G$1,"A","")
F1=INT(RAND()*4)
G1=INT(RAND()*6)+5

登入發表回應

japhenchen

iT邦超人 1 級 ‧ 2021-01-26 14:23:14

跟你上題一樣，先做好排列組合，把所有符合條件的牌組列舉，再按權重去加到卡牌列裡，再去隨機抽取，不要用完全隨機，而是抽完一副卡牌，再產生一組新的卡牌

線上遊戲的抽卡機制幾乎如此

回應 3
分享
檢舉

ccx12462000 iT邦新手 5 級 ‧ 2021-01-26 15:01:59 檢舉

我在嘗試自己做桌遊，有看到有範例是可以隨機產生牌組，那我想要技能也隨機生成不知道會有甚麼火花，所以研究方法，EX是印刷老闆跟我說的

japhenchen iT邦超人 1 級 ‧ 2021-01-26 15:06:40 檢舉

EXCEL我不愛用，但python就可以，晚點寫個例子，之前玩私服就有做過抽卡牌的腳本，大家的做法都是生成卡牌堆，全部被抽完再重新生成一個新堆，而不是完全隨機生成，這樣才能完全控制機率，而不是聽天由命

japhenchen iT邦超人 1 級 ‧ 2021-01-26 22:22:35 檢舉

#!/usr/bin/env python3
# -*- coding:utf-8 -*-
import random
def main():
    maxC = 1000 #樣本數最多
    Chaos = {
            'A': 10,
            'B': 22, 
            'C': 22,
            'D': 22, 
            'E': 22, 
            'F': 2
            }
    # Chaos 指的是每個技能出現的最大%數，總和100，自己調
    ChaosOrder = list() # 存放所有的排列組合
    Order = list()

    for x in Chaos:
        # 排列所有的組合
        for y in Chaos:
            if x[0] != y[0]:
                n = [x[0], y[0]]
                n.sort()
                if n not in ChaosOrder:
                    ChaosOrder.append(n)
    # 上段的結果會是 [A,B],[A,C],[A,D].....
    # 按隨機權重把所有的組合累加上去
    random.seed()
    for j in ChaosOrder: # 把排列好的牌組依技能權重相乘，再乘上樣本最大值1000
        # 如A=0.1，B=0.22，w = 0.1*0.22*1000 = 22(張)，加入Order牌組
        # A,F 則 w = 0.1*0.02*1000 = 2張，Order堆裡就只會有2張
        # ....以此推算
        w = (Chaos[j[0]]/100) * (Chaos[j[1]]/100)*maxC
        for z in range(int(w)):
            Order.append(j)
            # Order 就是最後的樣本數
    random.shuffle(Order) #打亂Order
    print(random.sample(Order,40)) #從Order裡抽出40張卡牌，Print出來

if __name__ == '__main__':
    main()

試驗結果每次都會不同，但可驗証的出來每個技能出現的機率接近Chaos所設

[['B', 'E'], ['B', 'D'], ['B', 'D'], ['B', 'E'], ['C', 'D'], ['B', 'D'], ['C', 'D'], ['C', 'D'], ['C', 'E'], ['D', 'E'], ['A', 'D'], ['B', 'E'], ['B', 'D'], ['B', 'D'], ['B', 'F'], ['B', 'E'], ['C', 'D'], ['C', 'D'], ['B', 'E'], ['A', 'C'], ['B', 'C'], ['C', 'E'], ['A', 'D'], ['C', 'E'], ['C', 'D'], ['B', 'C'], ['C', 'E'], ['B', 'C'], ['C', 'D'], ['A', 'E'], ['D', 'E'], ['A', 'C'], ['B', 'E'], ['D', 'E'], ['B', 'C'], ['C', 'E'], ['B', 'C'], ['B', 'E'], ['B', 'C'], ['B', 'E']]

```
#!/usr/bin/env python3
# -*- coding:utf-8 -*-
import random
def main():
    maxC = 1000 #樣本數最多
    Chaos = {
            'A': 10,
            'B': 22, 
            'C': 22,
            'D': 22, 
            'E': 22, 
            'F': 2
            }
    # Chaos 指的是每個技能出現的最大%數，總和100，自己調
    ChaosOrder = list() # 存放所有的排列組合
    Order = list()

for x in Chaos:
        # 排列所有的組合
        for y in Chaos:
            if x[0] != y[0]:
                n = [x[0], y[0]]
                n.sort()
                if n not in ChaosOrder:
                    ChaosOrder.append(n)
    # 上段的結果會是 [A,B],[A,C],[A,D].....
    # 按隨機權重把所有的組合累加上去
    random.seed()
    for j in ChaosOrder: # 把排列好的牌組依技能權重相乘，再乘上樣本最大值1000
        # 如A=0.1，B=0.22，w = 0.1*0.22*1000 = 22(張)，加入Order牌組
        # A,F 則 w = 0.1*0.02*1000 = 2張，Order堆裡就只會有2張
        # ....以此推算
        w = (Chaos[j[0]]/100) * (Chaos[j[1]]/100)*maxC
        for z in range(int(w)):
            Order.append(j)
            # Order 就是最後的樣本數
    random.shuffle(Order) #打亂Order
    print(random.sample(Order,40)) #從Order裡抽出40張卡牌，Print出來

if __name__ == '__main__':
    main()

```

試驗結果每次都會不同，但可驗証的出來每個技能出現的機率接近Chaos所設
```
[['B', 'E'], ['B', 'D'], ['B', 'D'], ['B', 'E'], ['C', 'D'], ['B', 'D'], ['C', 'D'], ['C', 'D'], ['C', 'E'], ['D', 'E'], ['A', 'D'], ['B', 'E'], ['B', 'D'], ['B', 'D'], ['B', 'F'], ['B', 'E'], ['C', 'D'], ['C', 'D'], ['B', 'E'], ['A', 'C'], ['B', 'C'], ['C', 'E'], ['A', 'D'], ['C', 'E'], ['C', 'D'], ['B', 'C'], ['C', 'E'], ['B', 'C'], ['C', 'D'], ['A', 'E'], ['D', 'E'], ['A', 'C'], ['B', 'E'], ['D', 'E'], ['B', 'C'], ['C', 'E'], ['B', 'C'], ['B', 'E'], ['B', 'C'], ['B', 'E']]

```

修改

登入發表回應