Illustration by Adit Bhargava

同一個問題可以用不一樣的演算法解決，那到底哪一個最好? 這時就需要一個"評量的指標"，這邊有兩個評量演算法好壞的指標

• 花的時間 (時間複雜度)
• 佔用記憶體空間

想當然爾，花的時間越少、佔記憶體空間越少就是越好的演算法！

實務上是用大 O 符號（Big O notation，以下文章都會用 Big O）來記錄時間複雜度的快慢。接下來讓我繼續用上一篇找書的情境來解釋

圖書館找書跟 Big O

今天你想要在圖書館找一本叫 "Lion King" 的書．有兩個選擇

1. 從第一個書櫃的第一本書開始找直到找到為止
2. 用圖書館裡電腦提供的搜索書本網站找

方法 1 會隨著書本數 (n) 增加，需要的時間就等比增加，時間複雜度是 Big O(n)；而方法 2 不管書本數 (n) 如何增加，他都不會被影響，永遠是 1 分鐘就可以找到，時間複雜度是 Big O(1)。

假如圖書館只有一本書，你可能覺得不需要特別在電腦上查。但當書本數 (n) 到達 100 本時，用電腦查就比一本一本找快了 100 倍。

總結一下 Big O

Big O 是用來描述一個演算法在輸入 n 個東西時，總執行時間與 n 的關係。

想知道更精確的解釋可以看維基百科

時間複雜度單位 ?

這裏順便補充一下，演算法多快不是以秒衡量而是步驟次數。因為每個人電腦速度不同，程式語言也不同，用秒計算顯然不夠客觀。

以圖書館例子就可以知道

// 從 10 本書裡面找 "Lion King"
// n = 10

// 方法1 一本一本找
// 步驟次數 = 10 次
get_book( )

// 方法2 電腦找
// 步驟次數 = 1 次
get_book( )

常見的時間複雜度

很不幸的，並沒有一個完美的演算法能解決所有的問題。遇到問題通常會希望演算法比 Big O(n²) 快，如果能到達 Big O(n) 甚至是 Big O(log n)、Big O(1) 就是更理想的。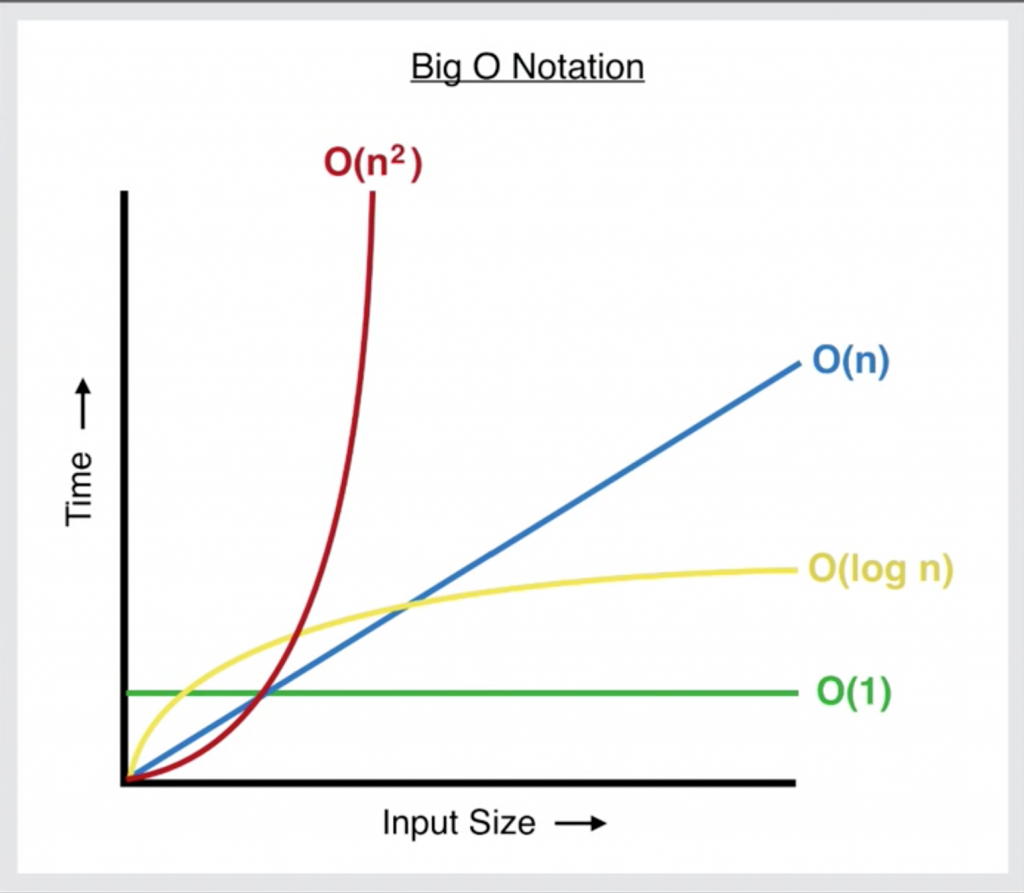

這張圖會看到當 n 到達一定數量，Big O(n²) 所花時間比 Big O(n) 多千倍甚至萬倍。所以寫出一個好的演算法是很重要的！

Big O(1)

輸入數量 n ，執行步驟 1。也就是不管你輸入多少東西，都會在同樣時間跑完。

我想在陣列 fruits 裡面抓第二個水果 fruits[1]，那不管陣列 fruits 裡面有 n 個水果 ，都不影響我抓水果的時間。

let fruits = ['Banana', 'Grapes', 'Watermelon', ...];
console.log(fruits[1]);  // 'Grapes'

Big O(n)

執行時間會跟著 n 等比例變多，最著名例子就是簡易搜尋。

我現在想吃 Grapes，但每個水果都被關在一模一樣的不透明箱子裡，所以我只好一個一個打開來檢查。

let fruits= ['Banana', 'Grapes', 'Watermelon', 'Avocado'];
for(let i = 0; i < fruits.length; i++){
	if(fruits[i] == 'Grapes'){
		console.log('耶 找到了')
	}else{
	  console.log('繼續找下一個箱子吧')
	}
}

看到這邊你可能會有疑問說，那假如第一個打開就是 Grapes，時間複雜度不就是 Big O(1) 了嗎？不對不對，Big O 會以最壞情況為前提，以這個例子來說最壞情況就是翻到最後一個箱子才會找到，所以時間複雜度是 Big O(n)。

Big O(log n)

輸入數量 n 時，執行步驟是 log n。這是第二棒的演算法。

相信大家早已忘了 log 是甚麼，這邊就來簡單複習一下

• log 4: 當 n = 4，程式會在 2 個步驟完成（4 = 2²）
• log 16: 當 n = 16 時，程式會在 4 個步驟完成（16 = 2⁴）
• log 32 ?? 相信大家都知道了

Big O(log n) 最有名的例子就是 binary search(後面文章會再詳細說明)。假如現在有 9 個水果按照英文字母排序放在不透明箱子裡，要從裡面找 Grapes。若用 Big O(n) 那就要找 9 次，但 Big O(log n) 只要 4 次就找到了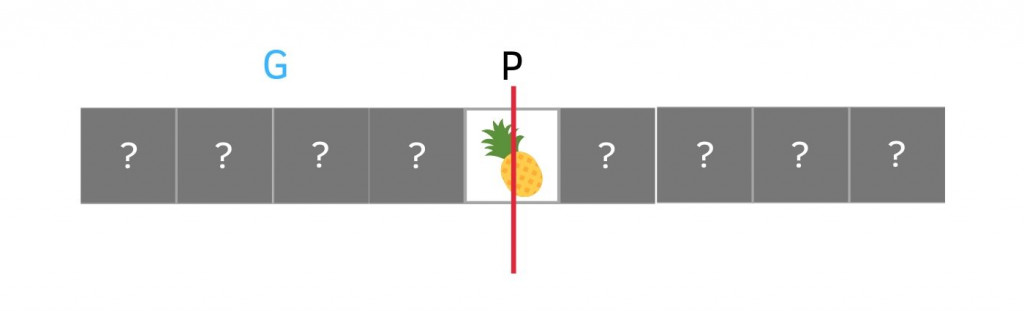

先從中間的箱子開始找，找到 pineapple, 而 G 字母比 P 前面所以往前找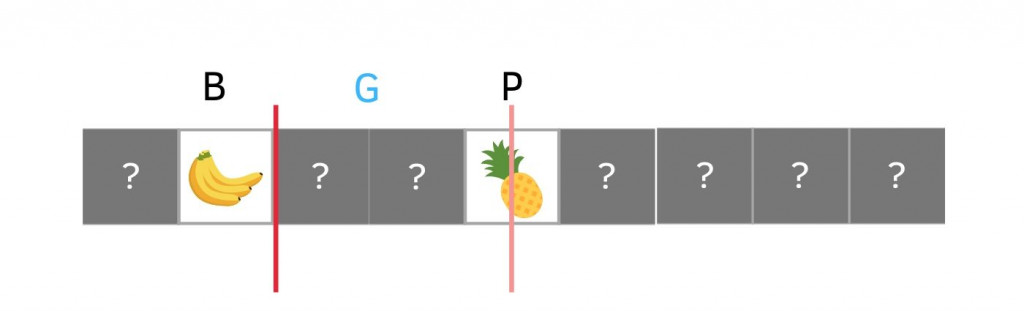

再從左半邊中間位置找，打開發現是 Banana. 而 G 比 B 後面所以往後找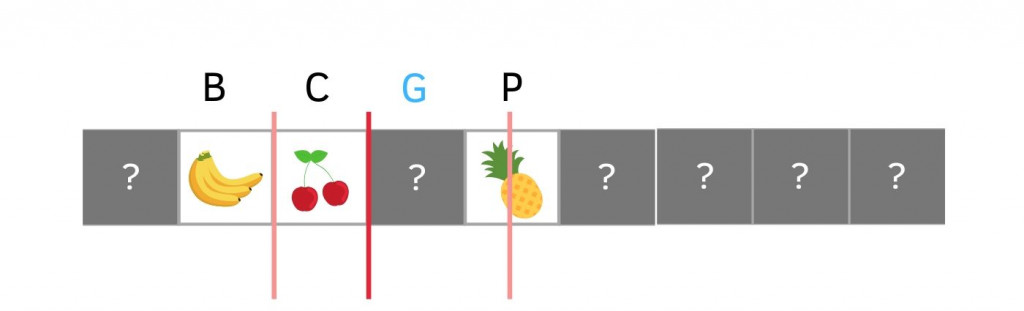

一樣的方法再從中間找，打開發現是 Cherry, G 比 C 後面所以往後找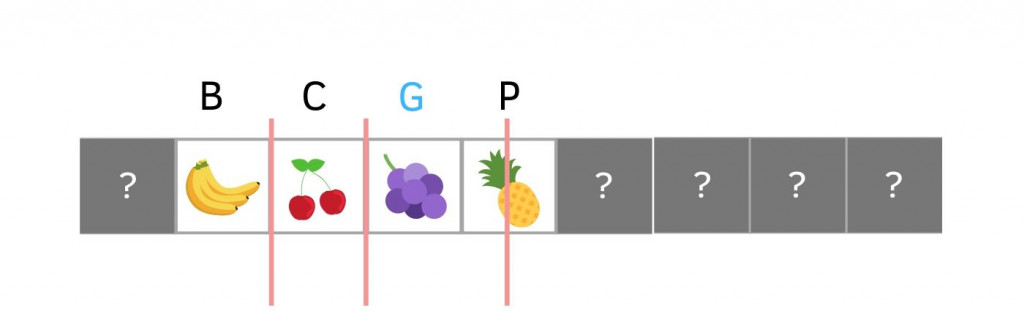

找到囉 !

後面篇章會在用實際程式解釋。

Big O(n²)

效能比較差演算法。例子像是選擇排序(之後章節會講到)。大致上來說，包了兩層 for loop 的都是 n² (慚愧的說我以前專案都這樣跑資料沒在管效能阿)。

for (var i = 0; i < len - 1; i++) {
  for (var j = i + 1; j < len; j++) {
		...
	}
}

Big O(2^n)

2 的 n 次方，效能很差。但例如 Fibonacci 就只能用這種演算法。通常寫 leetcode 你用到 Big O(2^n) 方法寫應該都是你寫錯方向了，一定會有別種效能較好演算法。

總結一下重點

• Big O: 評量演算法的時間複雜度
• 遇到問題時通常會希望演算法比 Big O(n²) 快，如果能到達 Big O(n)、Big O(log n)、Big O(1) 就是更理想的
• 演算法的速度不是以秒計算，而是以步驟次數
• 我們會以最壞狀況記錄 n
• 另外，時間複雜度會省略所有係數，例如 Big O(2n² + n)，會簡化成 O(n²)

參考文章

• 初學者學演算法｜談什麼是演算法和時間複雜度

如有錯誤或需要改進的地方，拜託跟我說。
我會以最快速度修改，感謝您

歡迎追蹤我的部落格，除了技術文也會分享一些在矽谷工作的甘苦。