今天要介紹的是樹，大致的樣子如下圖，其中樹的每個元素都稱為節點，樹最上方的節點稱為根節點，而節點之間上層節點為下層節點的父節點，下層節點為上層節點的子節點，如果一個節點底下沒有任何的子節點，我們稱為葉節點。

節點和其子節點可以構成子樹，如圖中的紅框部分。
一個節點的深度可由它祖先節點的數量推算出，例如14節點有25和34兩個祖先節點，其深度為2。
樹的高度則取決於所有節點深度的最大值，此圖高度為3。

樹(Tree)的應用例子

• HTML DOM
• Abstract Syntax Tree
• 資料夾結構
• JSON
• 臉書留言回覆，會有很多層

二元樹(Binary tree) 和 二元搜尋樹(Binary Search Tree)

這兩種樹在資料結構中相當常見，因此來稍微介紹它們:

二元樹每個節點最多只有兩個分支（即不存在分支度大於2的節點）的樹結構，通常分支被稱作「左子樹」或「右子樹」。

二元搜尋樹是指一棵空樹或者具有下列性質的二元樹：

• 若任意節點的左子樹不空，則左子樹上所有節點的值均小於它的根節點的值
• 若任意節點的右子樹不空，則右子樹上所有節點的值均大於它的根節點的值
• 任意節點的左、右子樹也分別為二元搜尋樹
• 沒有鍵值相等的節點

二元搜尋樹還有以下兩點特性:

• 節點資料是經過排序的
• 彈性的資料大小，可以隨意新增節點

二元搜尋樹的範例圖:

二元搜尋樹相關操作的動畫可以參考此連結

二元搜尋樹還衍伸出各種的 Tree

例如以下這幾種 Tree，有機會再詳細介紹它們。

平衡二元搜尋樹

它是一種每個節點的左右兩子樹高度差都不超過一的二元樹，例如附圖左邊的樹就是平衡二元搜尋樹，因為左右子樹高度相差一，但右邊的樹左右子樹高度相差二，就不算是平衡二元搜尋樹。出現此類樹是為了避免出現某些子樹出現過深，而有些子樹卻只有一兩層的情況，讓所有葉子的深度趨於平衡，如此即使最糟的情況下時間複雜度也能降低至 O(log n)。

要對一個樹做平衡的話，可以參考維基百科 Tree rotation 樹旋轉。

是對二元樹的一種操作，不影響元素的順序，但會改變樹的結構，將一個節點上移、一個節點下移。樹旋轉會改變樹的形狀，因此常被用來將較小的子樹下移、較大的子樹上移，從而降低樹的高度、提升許多樹操作的效率。

平衡二元搜尋樹的範例如 Red Black Tree、AVL Tree 都是平衡二元搜尋樹。

AVL Tree: 每一個節點的左子樹高度-右子樹高度只能是 -1、0、1

完全二元樹(Complete binary tree) / 完滿二元樹(Full binary tree)

• 完全二元樹: 除了最後一個階層的節點外，其他的節點都有兩個節點
• 完滿二元樹: 每個節點有0或2個子節點

在看完樹的介紹之後，我們來用 JavaScript 實作 樹吧!

先建立出節點和樹的類別出來:

class TreeNode {
  constructor(data, left = null, right = null) {
    this.data = data
    this.left = left
    this.right = right
  }
}

class Tree {
  constructor() {
    this.root = null
  }
}

之後透過新增節點，然後將節點加到節各節點的分支，便完成了

let n1 = new TreeNode(32);
let n2 = new TreeNode(92);
let n3 = new TreeNode(13);
let n4 = new TreeNode(44);
let n5 = new TreeNode(87);

let tree = new Tree();
tree.root = n1
n1.left = n2
n1.right = n3
n3.right = n4
n4.left = n5

產生的樹如下圖所示:

樹到這邊就完成實作，不過我們來試試多加一個 collect() 函式，將所有節點整理成陣列輸出

我們預設一開始的節點是root，然後節點陣列為空陣列，然後將目前找到的節點推入陣列，並將該節點的左右子節點作為參數，再次呼叫 collect() 函式進行遞迴。

class Tree {
  constructor() {
    this.root = null
  }

  // 使用遞迴去遍歷樹節點
  // 一開始的節點是root，然後節點陣列為空陣列
  collect(current = this.root, nodes = []) {
    if (current === null) {
      return nodes
    }
    nodes.push(current.data)

    this.collect(current.left, nodes)
    this.collect(current.right, nodes)
    return nodes
  }
}

用文字解說遞迴順序:

1. current = this.root，也就是根節點50，推入陣列 nodes
2. 找到根節點50的左節點43，推入陣列 nodes
3. 節點43再找左節點，但為 null，無新增任何東西，右節點也一樣為 null
4. 找到根節點50的右節點67，推入陣列 nodes
5. 節點67再找左節點，但為 null，無新增任何東西，不過找到有右節點，為節點81，推入陣列 nodes
6. 節點81找到左節點75，推入陣列 nodes，節點75左右子節點都是 null，便回傳最終的 nodes 陣列

這次實作的程式碼在以下連結:
https://github.com/a90100/javascript-data-structure/blob/master/day11-tree.js

二元搜尋樹的時間複雜度

• 插入節點、搜尋節點、移除節點: 最佳、平均 O(log n)，最差的狀況例如每層節點只有右節點的 Tree，或是都只有左節點的 Tree(形狀很奇怪XD) 為 O(n)

樹的走訪

樹的走訪主要分成兩種-BFS(廣度優先搜尋) & DFS(深度優先搜尋)，Tree 和 Graph 都可以執行這兩個演算法。

Breadth-First Search(BFS，廣度優先搜尋)

按照 Tree 的層級由上層往下層遍歷，每層的節點都訪問過後，就會往下一層的節點訪問。

BFS 函式實作

使用 quque 去儲存每層的節點，visited 儲存要回傳的節點陣列。

1. 第一層: 當前根節點為 10，將其子層的節點存在 queue
   quque: [6, 15]
   visited: [10]

//      10
//   6     15
// 3  8      20

2. 第二層，到 6 節點，存 3、8
   quque: [15, 3, 8]
   visited: [10, 6]

3. 第二層，到 15 節點
   quque: [3, 8, 20]
   visited: [10, 6, 15]

4. 第三層
   quque: []
   visited: [10, 6, 15, 3, 8, 20]

將上面的概念轉換成程式碼，可以寫出以下函式:

BFS() {
  let node = this.root;
  const data = [], queue = [];
  queue.push(node);

  while (queue.length) {
    node = queue.shift();
    data.push(node.value);
    if (node.left) queue.push(node.left);
    if (node.right) queue.push(node.right);
  }
  return data;
}

Depth-First Search(DFS，深度優先搜尋)

從演算法的名字"深度"可以知道和 BFS 是相對的關係，BFS 是橫向的一層層掃過搜尋，而 DFS 的確是相反，是從樹根不斷往子樹節點往下搜尋(縱向)，並且根據搜尋的順序還可以細分為以下幾種:

前序遍歷 (Preorder Traversal)

順序是根節點、左子節點、右子節點，根排在前面。

後序遍歷 (Postorder Traversal)

順序是左子節點、右子節點、根節點，根排在後面。

中序遍歷 (Inorder Traversal)

順序是左子節點、根節點、右子節點，根排在中間。

如果是遍歷的樹是二元搜尋樹的話，取出的節點會依照由小而大排序

層序遍歷 (Level-order Traversal)

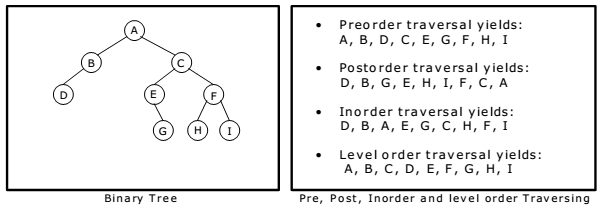
由根節點開始，到下層子節點，由左至右遍歷，並持續往下層遍歷至全部節點為止。可用 Queue 作為層序遍歷

Tree 的 BFS 和 DFS 比較

BFS

• 常搭配 Queue 實作
• 適合查找目標比較接近起始根節點的情況
• 因為 BFS 會由上層往下層遍歷節點，故需要消耗較多記憶體儲存

DFS

• 常搭配 Stack 實作
• 適合查找目標比較遠離起始根節點的情況
• 消耗較少記憶體儲存節點，但很深的(例如只有左節點那種) Tree 也會和 BFS 消耗得差不多

而兩者的時間複雜度都是 O(v + e)，v 是節點數量，e 是邊的數量。

以上就是這次的樹 (Tree) 介紹，明天將會介紹樹的一些相關操作函式!