這篇會先簡單介紹 Graph，真的簡單寫一下
後面就會再從樹開始，盡可能寫幾個樹，看可以撐到哪天QQ

Directed and Undirected Graphs

Graph 用 G = (V, E) 表示。
V 表示 vertex (/node) set V = {v_0 , v+1 , ... , v_{V −1}}
E 表示 edge (/arc) set E = {e_0 , e_1 , ... , e_{E −1}}
而 e_i ∈ E 連接一至兩個 vertexe(s)

如果每個 e_i ∈ E 中的 e_i =(v_{is}，v_{id})，也就是有表示方向，則圖 G 稱為有向圖。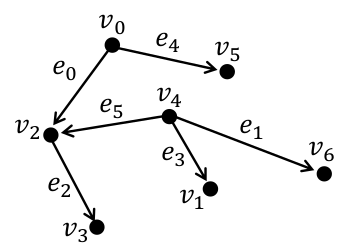

如果每個 e_i ∈ E 只是一個具有兩個頂點的集合：e_i = {v_{i1}, v_{i2}}的集合，則圖G稱為無向圖。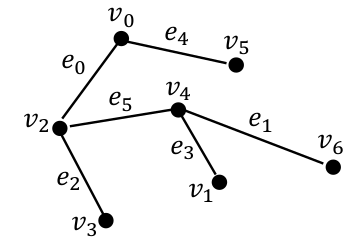

Connectivity of Graph

如果圖 G =（V，E）任何 v_s, v_d∈V，存在從 v_s 到 v_d 的之間一對一連接的邊，則稱為 connected。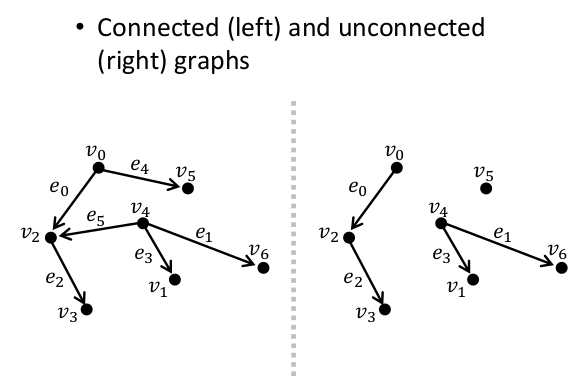

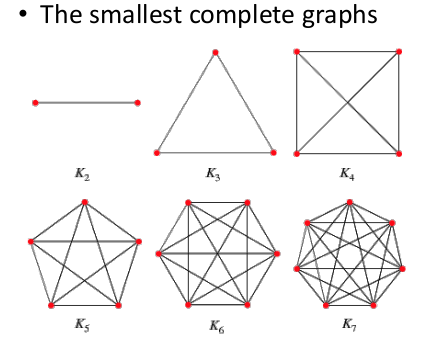
完全圖是每對頂點之間都恰連有一條邊的簡單圖。n 個端點的完全圖有 n 個端點及 n(n-1)/2 條邊，以 K_n 表示。