我們已經知道了如何創建一個物體並上色或貼上紋理,給他們一些細節的表現,但是這些都只是靜態的表現。我們可以嘗試在每個 frame 都重新配置 VBO 使他們動起來,但是這太繁瑣且耗效能。更好的方法就是用使用(多個)矩陣(Matrix) 將座標 轉換(Transform) 過去。
注意以下有較多的數學
向量最基本的定義就是一個方向。或者更正式的說,向量有一個方向(Direction)和大小(Magnitude,也叫做長度)。
向量可以在任意維度(Dimension)上,但是我們通常只使用2至4維。如果一個向量有2個維度,它表示一個平面的方向(想像一下2D的圖像),當它有3個維度的時候它可以表達一個3D世界的方向。
由於向量表示的是方向,起始於何處並不會改變它的值。下圖我們可以看到w向量和v向量是相等的,儘管他們的起始點不同:
由於向量是一個方向,我們通常設定這個方向的原點為(0, 0, 0),然後指向一個方向,對應一個點,使其變為位置向量(Position Vector)。比如說位置向量(3, 5)在圖像中的起點會是(0, 0),並會指向(3, 5)。我們可以使用向量在2D或3D空間中表示方向與位置。
標量 Scalar

反向

向量加法


向量減法


長度

單位向量

定義

一些性質

單位向量內積: 
投影


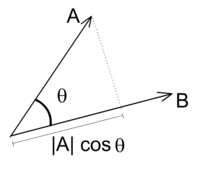
把每個分量相乘
e.g.
用反餘弦 $\cos^{-1}$ 可以求得向量夾角

用來求與兩向量垂直的向量之方向,在計算三維空間中平面的垂直方向。


計算
$m\times n$ 的矩形陣列,裏頭的元素可以是數字、符號或算式。

加法、減法
Scalar (glm)


矩陣加減


Scalar 標量乘法

矩陣乘法
 只有 b = c 才可以相乘,產出
只有 b = c 才可以相乘,產出 
沒有交換律,

運算規則
交換律

分配律


單位矩陣 Identity Matrix

 稱作均勻縮放(Uniform Scale)
稱作均勻縮放(Uniform Scale)


所以的位移值( )都會乘上 w,w 稱作齊次座標(Homogeneous Coordinates),它讓我們可以用矩陣乘法來表示向量位移
)都會乘上 w,w 稱作齊次座標(Homogeneous Coordinates),它讓我們可以用矩陣乘法來表示向量位移
旋轉會有角(Angle),而角可以用角度(Degree)及弧度(Radian)表示,角度比較直觀,但電腦計算通常都用弧度
角度 = 弧度 * (180.0f / PI)
弧度 = 角度 * (PI / 180.0f)

在 3D 空間中旋轉需要:角(Angle)跟旋轉軸(Rotation Axis)
沿 x 軸旋轉
沿 y 軸旋轉
沿 z 軸旋轉
我們可以把三軸的旋轉組合起來,達成任意的旋轉,但這會產生:萬象鎖(Gimbal Lock)的問題產生

這裡有很好的解釋
[ ] https://silverwind1982.pixnet.net/blog/post/345691427-gimbal-lock---%E8%90%AC%E5%90%91%E9%8E%96
[ ] https://krasjet.github.io/quaternion/bonus_gimbal_lock.pdf
更好的模型是:沿著任意的軸,例如單位向量 $(0.662, 0.2, 0.7222)$,而不是拆成三個軸的選轉組合
 代表任意旋轉軸
代表任意旋轉軸
多個變換矩陣可以用乘法融合到一個矩陣中。例如,先縮放兩倍、再位移$(1,2,3)$
矩陣乘法是從最右邊開始,依序往左乘,所以是最右邊的操作最先發生。

不同的操作之間可能相互影響,依照縮放、旋轉、位移的順序組合矩陣,否則操作間會相互影響


GLM是OpenGL Mathematics的縮寫,它是一個只有頭文件的庫,也就是說我們只需包含對應的頭文件就行了,不用鏈接和編譯。
我們需要的GLM的大多數功能都可以從下面這3個頭文件中找到:
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>
我們來看看是否可以利用我們剛學的變換知識把一個向量$(1, 0, 0)$位移$(1, 1, 0)$個單位
glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 trans(1.0f);
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
printf("%d %d %d\n", vec.x, vec.y, vec.z);
縮放 0.5 倍,逆時針選轉 90 度
glm::mat4 trans;
trans = glm::rotate(trans, glm::radian(90.f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));
接下來我們要更改我們的 Shader。
我們在前面簡單提到過 GLSL 裡也有一個mat4類型。所以我們將修改頂點著色器讓其接收一個mat4的uniform變量,然後再用矩陣uniform乘以位置向量:
#version 450 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aVertColor;
layout (location = 2) in vec2 aTexCoord;
out vec3 VertColor;
out vec2 TexCoord;
uniform mat4 vTransform;
void main()
{
gl_Position = vTransform * vec4(aPos, 1.0);
TexCoord = aTexCoord;
VertColor = aVertColor;
}
然後將矩陣傳給 Shader。
int transformLoc = glGetUniformLocation(program, "vTransform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));
如果以上的程式都沒有錯的話會跑出以下的結果
接著我們試試看能不能隨著時間旋轉他
glm::mat4 trans(1.0f); // identity matrix
static float rotate_degree = 90.f;
rotate_degree = fmod(mixClk.getElapsedTime().asMilliseconds()/10, 360);
trans = glm::rotate(trans, glm::radians(rotate_degree), glm::vec3(0.0, 0.0, 1.0));

完整的code在這裡
https://learnopengl.com/Getting-started/Transformations
