昨天已經挑戰完矩陣的加和減了，今天來挑戰稍難一點的矩陣乘法，再開始之前先來簡單介紹矩陣的乘法吧~~
對於矩陣來說跟一般數字的四則運算有著很大的差異，就是加或減與乘跟除的不同，矩陣的乘除比較複雜，除法是要乘上反方陣，這個內容還蠻難的，我們先來討論乘法，但是要小心兩個矩陣相乘並不是隨便大小都能夠相乘而是要滿足
MXN X NXM = MXM (M:代表列的數目 N:代表行的數目) 這個規則，因為矩陣是有兩個維度並不能只用一個維度來判斷是否能相乘。乘法簡單來說就是第一個矩陣的列乘上第二個矩陣的行，依照這個規則我寫出以下的程式

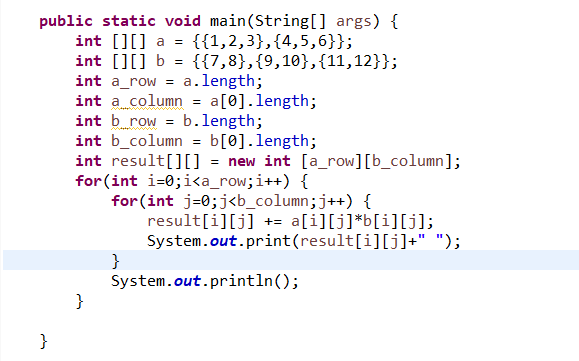
這是我一開始寫的感覺想法應該是對的但怎麼答案怪怪的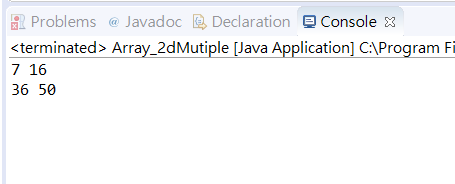

基本上看到第一個元素就感覺有問題了，因此為了想清楚這題我把所有元素列出來了
基本上就是一個元素一個個乘再加起來，至於a[0][0],a[0][1],a[1][0].....都是代表在二維陣列當中的位置
索引值都是從0開始，前面的數字代表列後面代表行，以a[0][1]為例，代表的是第一列第二行；a[1][0]代表的是第二列第一行依此類推。
從上面的圖片能知道一件事，二個迴圈不夠，為什麼呢？
因為兩個迴圈頂多只能從二個二維陣列當中找出值來做相乘，但是矩陣乘法是要將相乘完的結果再做相加，因此需要用到第三個迴圈

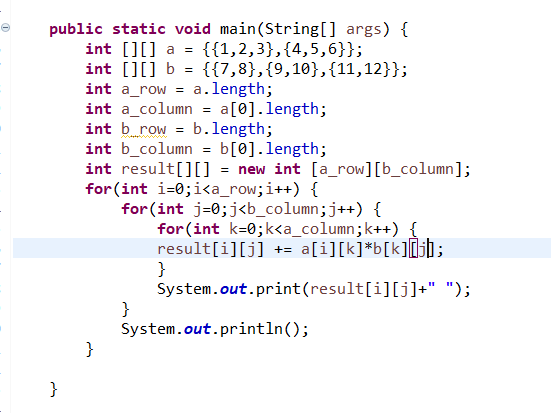
看起來很複雜對吧，很少會用到三層迴圈，因此我們必須來好好談談這三個迴圈分別代表什麼
第一層代表的是找a的列；第二層代表的是找b的行；第三層代表的是需要加幾次
從我手寫的那張可以發現需要加3次，而3又是從而來的呢？不就是a的行或是b的列數嗎發現了嗎，兩個數目必須相同否則無法做矩陣相乘，因為要滿足MXN X NXM = MXM 這個規則
因此迴圈裡的內容就簡單啦 a[i][k]*b[k][j]是不是就能寫出來了呢，最後只要把它們加起來存入result[i][j]484就搞定了!!!!