Given two integers dividend and divisor, divide two integers without using multiplication, division, and mod operator.

Return the quotient after dividing dividend by divisor.

The integer division should truncate toward zero, which means losing its fractional part. For example, truncate(8.345) = 8 and truncate(-2.7335) = -2.

Note:

Assume we are dealing with an environment that could only store integers within the 32-bit signed integer range: [−2^31, 2^31 − 1]. For this problem, assume that your function returns 231 − 1 when the division result overflows.

Example 1:

Input: dividend = 10, divisor = 3
Output: 3
Explanation: 10/3 = truncate(3.33333..) = 3.

Example 2:

Input: dividend = 7, divisor = -3
Output: -2
Explanation: 7/-3 = truncate(-2.33333..) = -2.

Example 3:

Input: dividend = 0, divisor = 1
Output: 0
Example 4:

Input: dividend = 1, divisor = 1
Output: 1

Constraints:

-2^31 <= dividend, divisor <= 2^31 - 1
divisor != 0

Solution:
被除數 / 除數 = 商數
return 商數 <-- 取整數即可
如果 商數大於 2^32 -1 則回傳 2^32 -1

Code:

class Solution:
    def divide(self, dividend: int, divisor: int) -> int:
        quotient = dividend / divisor
        print(int(quotient))
        if int(quotient) > (pow(2,31)-1):
            return pow(2,31)-1
        return int(quotient)

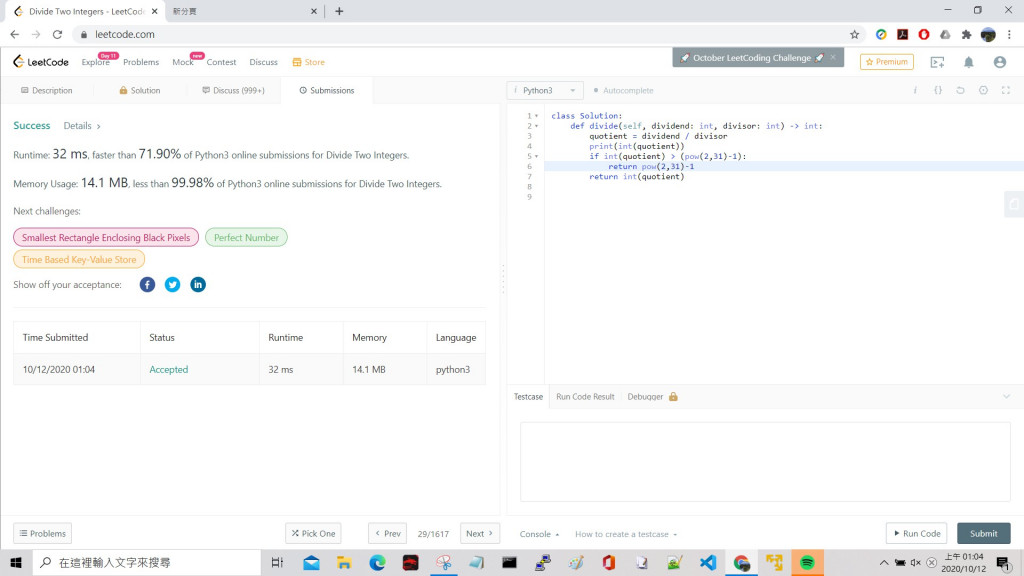
Result: