終於寫完基本DFS跟BFS了~~
今天開始進入正題(?
今天講的是多源最短路徑算法

例題&算法

直接用一題例題來解釋：
743. 网络延迟时间
題目敘述：
一張有向圖，權重代表傳遞時間(大於0)，給定一個起點，求起點出發，要多久時間才能使所有節點收到訊號??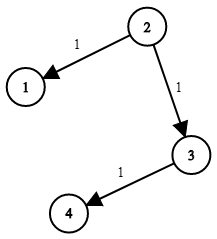

输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出：2
((圖與測試資料來自力扣))
這題要求每一個節點與起點的最短路徑，並返回最大的那一個，就是最短的時間內所有節點收到訊號的時間~~

[法一]Floyd-Warshall

思路：i->j的路徑如果i->k->j比i->j快，那就選擇i->k->j。
實現就是遍歷所有節點k，找尋是否有i->j可以鬆弛

for(int k=0; k<n; ++k){
    for(int i=0; i<n; ++i){
        for(int j=0; j<n; ++j){
            dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
        }
    }
}

WHY?

為什麼遍歷所有節點k，找尋是否有i->j可以鬆弛，路徑就已經都是最短了??
對於節點k來說，如果這個節點要去對邊鬆弛，那就必須找到一個i->k->j比i->j快(短)，也是這個演算法的思路。當每個k都已經把所有i->j的可能((k節點可能鬆弛的邊))找完了，那這個k節點就不可能再去鬆弛邊了，當所有節點都不可能再對邊鬆弛了，那每個i->j都是最短路徑了~~

例題完整程式碼

#define vt vector
#define pb push_back
#define iipair pair<int, int>
#define cipair pair<char, int>
#define icpair pair<int, char>
#define ispair pair<int, string>
#define sipair pair<string, int>
#define MOD 1e9+7
#define iMat vector<vector<int>>
#define cMat vector<vector<char>>
#define ll long long
#define mp make_pair
class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int N, int K) {
        vt<vt<int>> adj(N+1, vt<int>(N+1, 6001));
        for(int i = 1; i<=N; ++i){
            adj[i][i] = 0;
        }
        for(int i = 0; i<times.size(); ++i){
            adj[times[i][0]][times[i][1]] = times[i][2];
        }
        for(int k = 1; k<=N; ++k){
            for(int i = 1; i<=N; ++i){
                for(int j = 1; j<=N; ++j){
                    adj[i][j] = min(adj[i][j],adj[i][k]+adj[k][j]);
                }
            }
        }
        int res = 0;
        for(int i = 1; i<=N; ++i){
            if(adj[K][i]==6001) return -1;
            res = max(res, adj[K][i]);
        }
        return res;
    }
};

這是屬於多源的最短路徑算法，明天講單源最短路徑~~