
Traversal翻譯成中文就是遍歷的意思,如果要遍歷tree的每個節點的話,會有兩種方式,Breadth-First Tree Traversal和Depth-First Tree Traversal。
Breadth-First Tree Traversal 也被稱作Level Order Tree Traversal,利用廣度優先搜尋(Breadth-First Search, BFS)的方式來遍歷每個節點,概念非常容易理解 ,就是將每一層的節點由左至右依序取出。
從某個節點出發,接下來走訪相鄰節點,同一層的都走訪完了就往下一層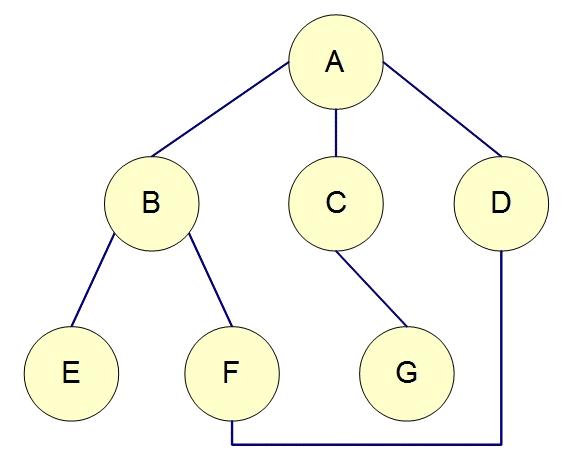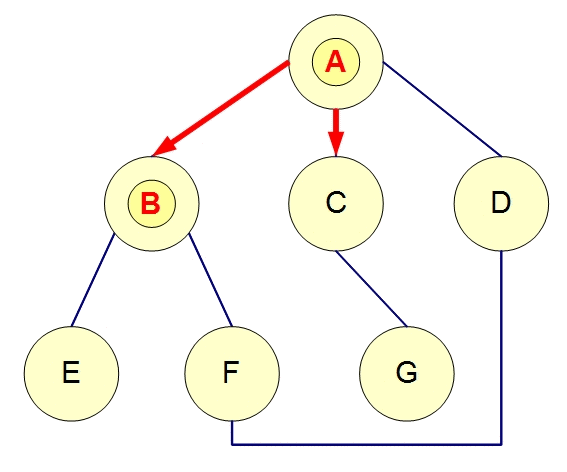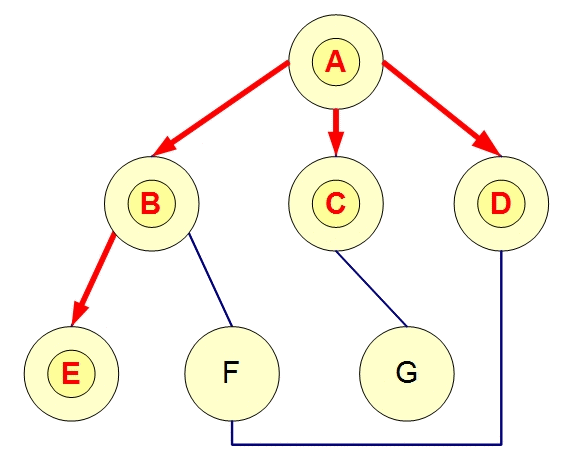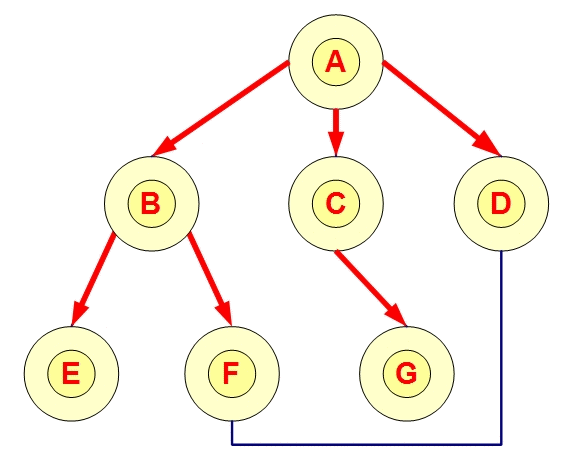
圖片來源:BreadthFirstSearch
假設我們現在有顆Binary Tree如下圖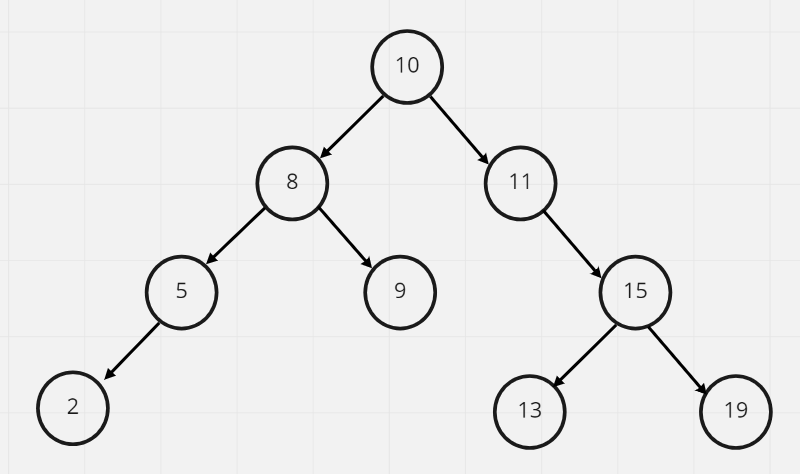
用廣度優先搜尋的方式走訪的步驟為:
1.第1層 取出10
2.第2層 取出8, 11
3.第3層 取出5, 9 ,15
4.第4層 取出2, 13, 19
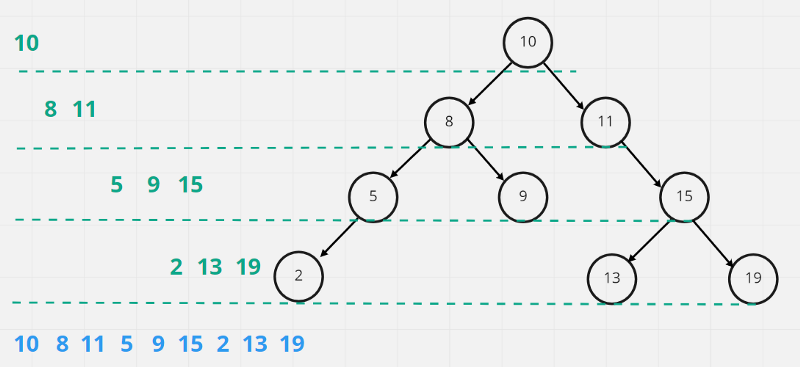
最後取得陣列[10, 8, 11, 5, 9, 15, 2, 13, 19]
用js實作Breadth-First Tree Traversal:
bftt(node) {
if (node === null) return;
this.queue.push(node);
for (let i = 0; i < this.queue.length; i++) {
let currentNode = this.queue[i];
if (currentNode === null) continue;
if (currentNode.left !== null) {
this.queue.push(currentNode.left);
}
if (currentNode.right !== null) {
this.queue.push(currentNode.right);
}
}
}
tree.bftt(tree.root)
採用的是深度優先搜尋(Depth-First-Search,DFS)的方式來遍歷節點,Depth-First Tree Traversal又分為三種,這三種非常類似,但遍歷的順序不同。
深度優先搜尋演算法(英語:Depth-First-Search,DFS)是一種用於遍歷或搜尋樹或圖的演算法。這個演算法會儘可能深的搜尋樹的分支。當節點v的所在邊都己被探尋過,搜尋將回溯到發現節點v的那條邊的起始節點。這一過程一直進行到已發現從源節點可達的所有節點為止。如果還存在未被發現的節點,則選擇其中一個作為源節點並重複以上過程,整個行程反覆進行直到所有節點都被存取為止。這種演算法不會根據圖的結構等資訊調整執行策略(引用自wikipedia)
看完維基百科的解釋真的是似懂非懂,這邊我會想像是摸著牆在走迷宮,發現走到底了,就回頭找另一道牆繼續探索,只是靠牆的順序有所差異(先靠左或是先靠右)。
順序: 根節點 → 左節點 →右節點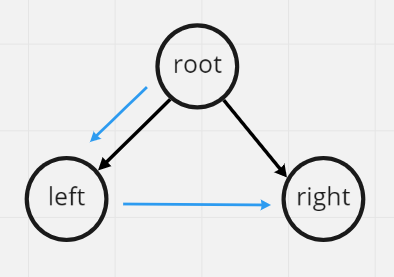
實際用PreOrder走訪一次Binary Tree的話,順序如下圖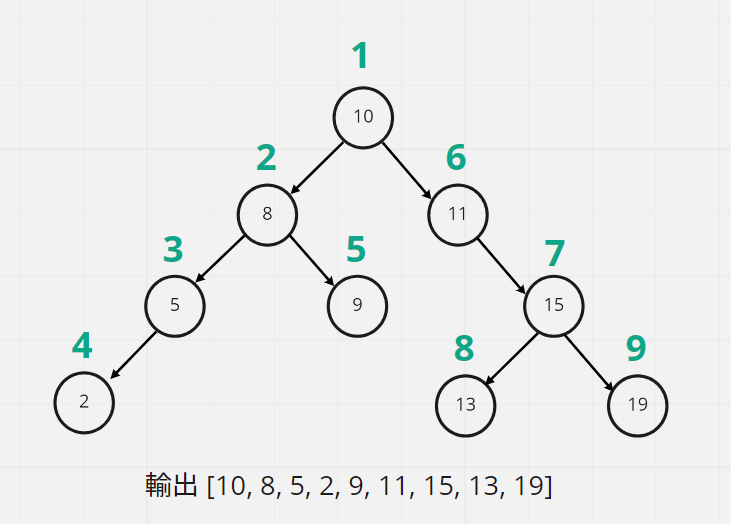
綠色的數字為遍歷的順序用
js實作PreOrder
preOrder(node) {
if (node === null) return;
this.queue.push(node.value);
//用遞迴來遍歷節點
this.preOrder(node.left);
this.preOrder(node.right);
}
tree.preOrder(tree.root);
順序: 左節點 → 根節點 →右節點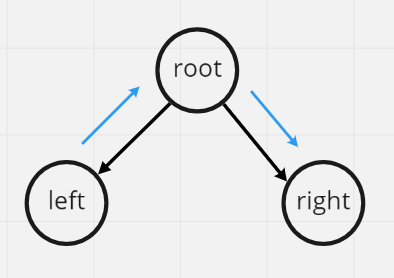
實際用InOrder的方式走訪一次二元樹的話順序如下圖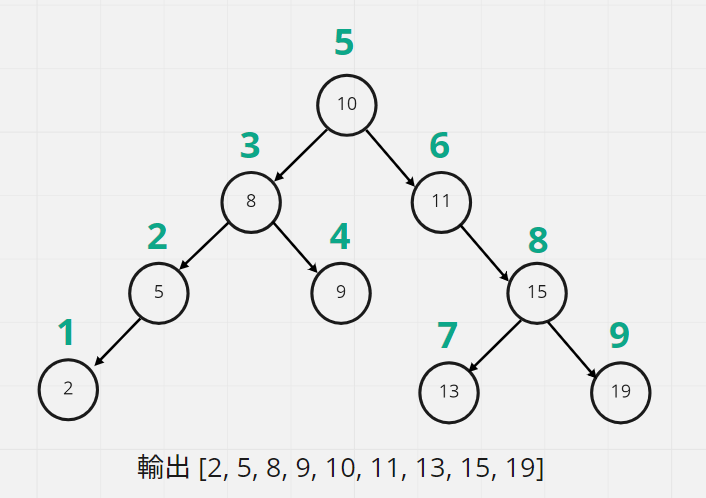
綠色的數字為遍歷的順序
用js實作InOrder
inOrder(node) {
if (node === null) return;
//用遞迴來遍歷節點
this.inOrder(node.left);
this.queue.push(node.value);
this.inOrder(node.right);
}
tree.inOrder(tree.root);
順序: 左節點 → 右節點 → 根節點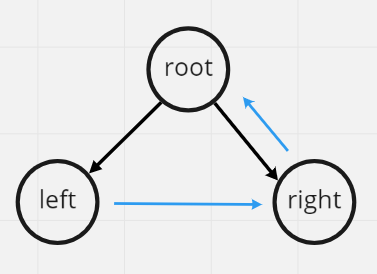
實際用PostOrder走訪一次Binary Tree的話順序如下圖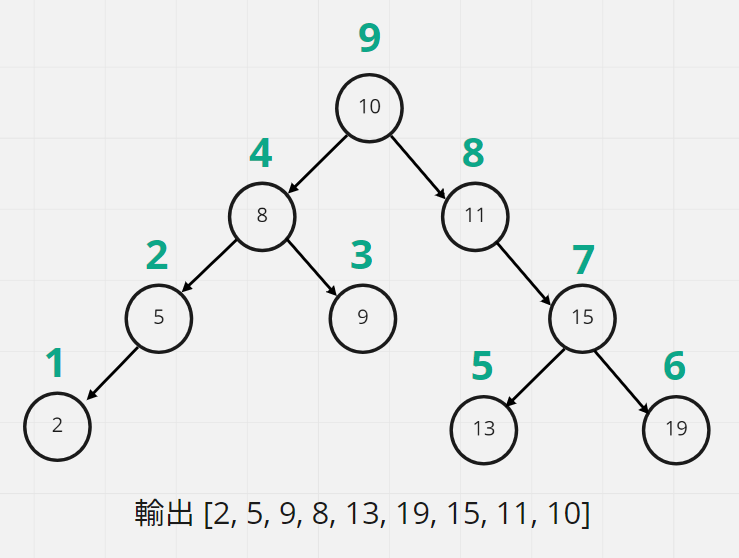
用js實作PostOrder
postOrder(node) {
if (node === null) return;
//用遞迴來遍歷節點
this.postOrder(node.left);
this.postOrder(node.right);
this.queue.push(node.value);
}
tree.postOrder(tree.root);
下面這張圖簡易的說明了BFS和DFS兩者的差異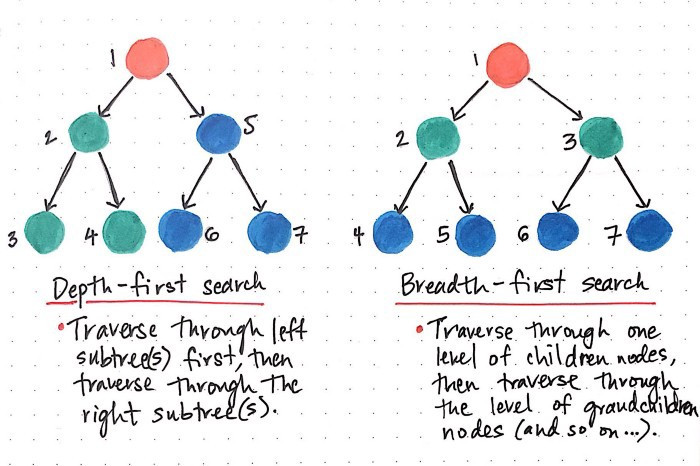
圖片來源:https://medium.com/basecs/breaking-down-breadth-first-search-cebe696709d9
第一種方式使用遞迴,利用Binary tree的特性(當前節點的右子節點會比自己大 ,左子節點會比自己小),如果目標值比當前節點還大的話就把當前節點的右節點作為參數傳入函式,反之就把左節點傳入,不斷呼叫自己,直到找到節點或是找不到就中止遞迴。
const searchRecursively = (node, target) => {
if (node === null || target === node.value) return node;
if (target < node.value) {
return searchRecursively(node.left, target);
}
if (target > node.value) {
return searchRecursively(node.right, target);
}
};
searchRecursively(tree.root, 13);
執行結果如下,找得到就回傳該節點,若找不到就回傳null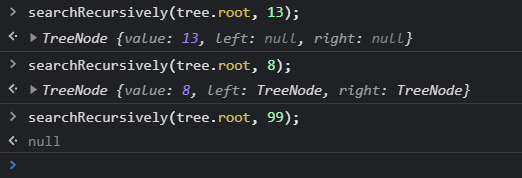
第二種方式用迴圈,假如目標值比當前節點還大的話,就把當前節點移動到右邊的子節點,反之則移動到左邊的節點,直到找到值或是找不到就跳出迴圈。
const searchIteratively = (node, target) => {
while (node !== null && target !== node.value) {
if (target < node.value) {
node = node.left;
} else {
node = node.right;
}
}
return node;
};
searchIteratively(tree.root, 8);
執行結果如下,找得到就回傳該節點,若找不到就回傳null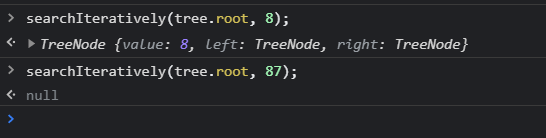
Binary Tree - Traversal完整的程式碼如下(包含tree的建立)
class TreeNode {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
this.queue = [];
}
insertNode(value) {
let current = new TreeNode(value);
let target = null;
let nowPos = this.root;
while (nowPos !== null) {
target = nowPos;
if (current.value < nowPos.value) {
nowPos = nowPos.left;
} else {
nowPos = nowPos.right;
}
}
if (target === null) {
this.root = current;
} else if (current.value < target.value) {
target.left = current;
} else {
target.right = current;
}
}
bftt(node) {
if (node === null) return;
this.queue.push(node);
for (let i = 0; i < this.queue.length; i++) {
let currentNode = this.queue[i];
if (currentNode === null) continue;
if (currentNode.left !== null) {
this.queue.push(currentNode.left);
}
if (currentNode.right !== null) {
this.queue.push(currentNode.right);
}
}
}
preOrder(node) {
if (node === null) return;
this.queue.push(node.value);
//用遞迴來遍歷節點
this.preOrder(node.left);
this.preOrder(node.right);
}
inOrder(node) {
if (node === null) return;
//用遞迴來遍歷節點
this.inOrder(node.left);
this.queue.push(node.value);
this.inOrder(node.right);
}
postOrder(node) {
if (node === null) return;
//用遞迴來遍歷節點
this.postOrder(node.left);
this.postOrder(node.right);
this.queue.push(node.value);
}
}
let tree = new BinarySearchTree();
tree.insertNode(10);
tree.insertNode(8);
tree.insertNode(11);
tree.insertNode(5);
tree.insertNode(9);
tree.insertNode(15);
tree.insertNode(2);
tree.insertNode(19);
tree.insertNode(13);
console.log("BST", tree);
tree.bftt(tree.root);
tree.preOrder(tree.root);
tree.inOrder(tree.root);
tree.postOrder(tree.root);
console.log(tree.queue);
const searchRecursively = (node, target) => {
if (node === null || target === node.value) return node;
if (target < node.value) {
return searchRecursively(node.left, target);
}
if (target > node.value) {
return searchRecursively(node.right, target);
}
};
const searchIteratively = (node, target) => {
while (node !== null && target !== node.value) {
if (target < node.value) {
node = node.left;
} else {
node = node.right;
}
}
return node;
};
searchRecursively(tree.root, 13);
searchIteratively(tree.root, 8);
?在最差的情況下, 時間複雜度是O(n)
?在最佳的情況下 , 時間複雜度是O(1)
?在平均情況下,時間複雜度為 O(log n)
不管是Tree Traversal或是在tree中尋找特定的值都是leetcode蠻常見的考題,只要可以掌握這些核心觀念,在解題的時候就會比較得心應手。
參考資料:Tree Traversals
