想必大家在刷leetcode時候，刷到特定的題目的時候都曾經看過這樣的圖片，這就是Binary tree，但在認識Binary tree之前，讓我們先來認識tree這種資料結構吧!

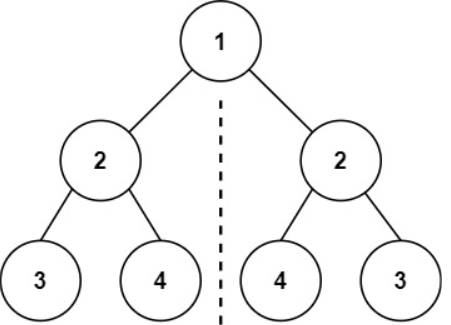
圖片來源:101. Symmetric Tree

Tree

是一種抽象的資料結構，由一個以上的節點所組成，每個節點可以有多個子節點，最頂端的根節點稱為root ，最下面的層級的節點稱為leaves(2, 1, 7 …)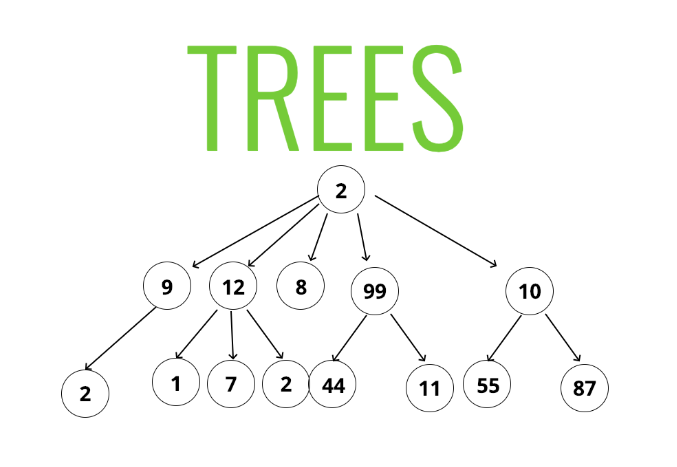

圖片來源:working-with-trees

而節點與節點之間的關係名詞可以參考下圖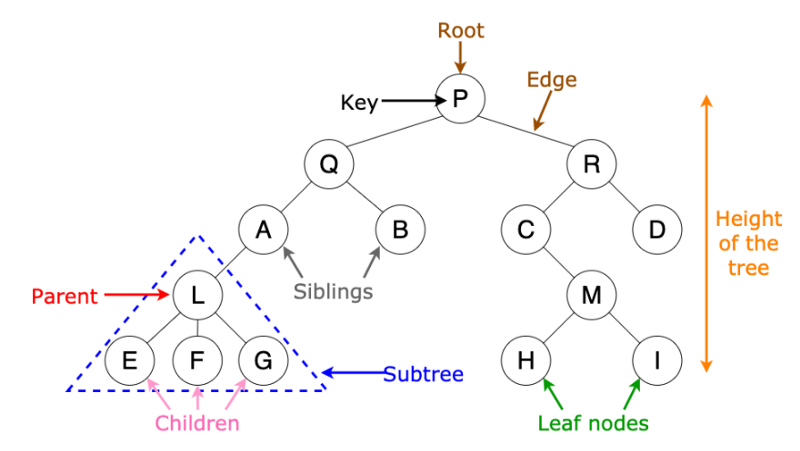

圖片來源:understanding-binary-search-trees-4d90

• Root - 根節點，最上層的節點
• Edge- 節點與節點之間的連結
• Parent - 父節點，與節點相鄰的上層節點
• Children - 子節點，與節點相鄰的下層節點
• Siblings - 兄弟節點，層級在同一層，而且擁有共同的父節點
• Leaf nodes - 葉子節點，沒有子節點的節點
• Subtree - 子樹，該節點以及其左右子節點
• Height - 樹的高度，可以解讀為樹有幾層

Binary Tree(二元樹)

每個節點的子節點最少0個，最多2個 ，每個節點會紀錄三種資料

• 自己本身的值
• left-child，左子節點
• right-child，右子節點

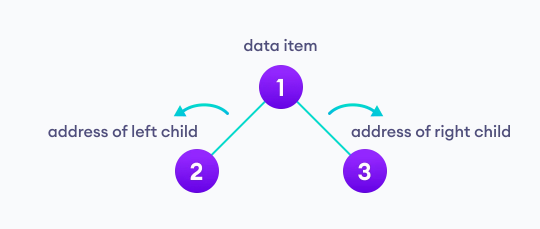
圖片來源:Binary Tree

與一般樹的比較如下，Binary Tree每個節點最多就是兩個子節點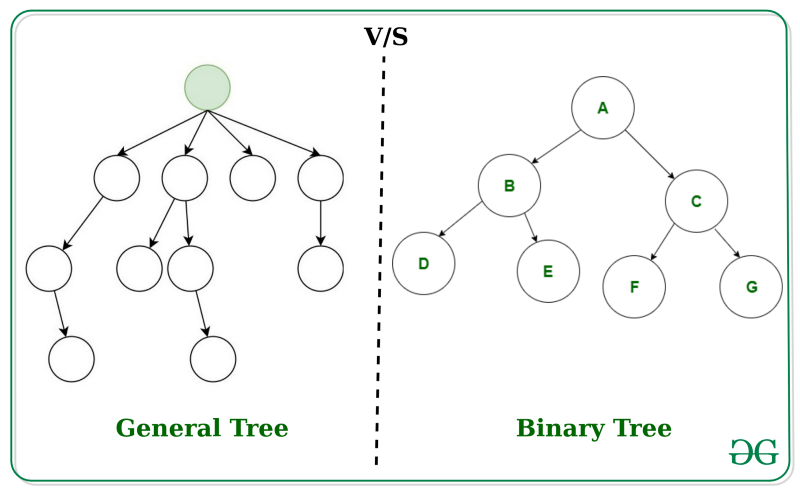

圖片來源:difference-between-general-tree-and-binary-tree

Binary Tree的種類

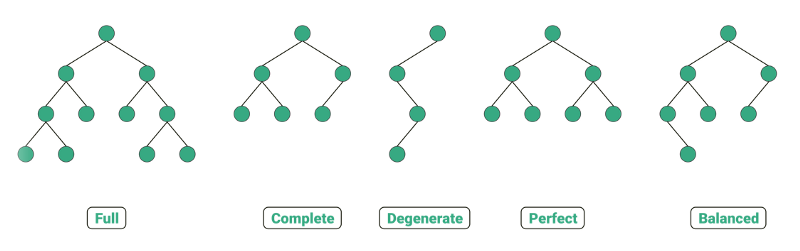
圖片來源:5-types-of-binary-tree-with-cool-illustrations

full

• 所有的leaf node都在同一個層級
• 每個節點的子節點為0個或是2個

Complete

• 除了最後一層leaf node之外，每層都是填滿的狀態
• 所有的leaf node都會向左靠攏，因此leaf nodes有可能會沒有右邊的兄弟節點

Degenerate

• 每個節點只會有一個右子節點或是左子節點

Perfect

• 所有的leaf node都在同一個層級
• 除了leaf node之外，每個節點都有兩個子節點

Balance

• 左子樹和右子樹的層級相差不超過1

Skewed 

• 每個節點固定只有右子節點或左子節點，如下圖
  
  Skewed Binary Tree,圖片來源:binary-tree

Binary Search Tree(縮寫BST) - 二元搜尋樹

具有Binary Tree的特性，每個節點的子節點不超過2個，除此之外，左邊的子節點必定小於根節點，右邊的子節點必定大於根節點，因此整棵樹最左邊的節點必定是最小的，最右邊的節點必定是最大的，也因為Binary Search Tree這樣的特性，所以不管是新增節點、刪除節點、搜尋節點的時間複雜度都是O(log n)。

圖片來源:implementing-binary-search-tree

用js實作出Binary Search Tree

class TreeNode {
    constructor(value) {
        this.value = value;
        this.left = null;
        this.right = null;
    }
}

class BinarySearchTree {
    constructor() {
        this.root = null;
        this.queue = [];
    }
    insertNode(value) {
        let current = new TreeNode(value);
        let target = null;
        let nowPos = this.root;
        while (nowPos !== null) {
            target = nowPos;
            if (current.value < nowPos.value) {
                nowPos = nowPos.left;
            } else {
                nowPos = nowPos.right;
            }
        }
        if (target === null) {
            this.root = current;
        } else if (current.value < target.value) {
            target.left = current;
        } else {
            target.right = current;
        }
    }
}

let tree = new BinarySearchTree();
tree.insertNode(10);
tree.insertNode(8);
tree.insertNode(11);
tree.insertNode(5);
tree.insertNode(9);
tree.insertNode(15);
tree.insertNode(2);
tree.insertNode(19);
tree.insertNode(13);

如果consolo.log(tree)可以看到我們成功用物件模擬出一顆Binary Search Tree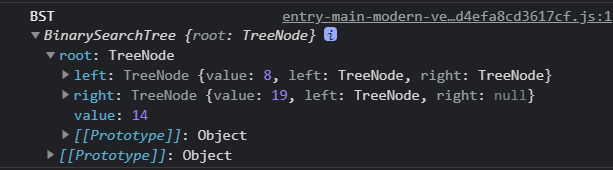

Binary Heaps - 二元堆積

Binary Heaps又分為Min-Heaps 和 Max-Heaps，適合用來找最小值或最大值

• Min-Heaps :每個節點都會比自己的子節點還小，因此根節點會是最小值
• Max-Heaps:每個節點都會比自己的子節點還大，因次根節點會是最大值

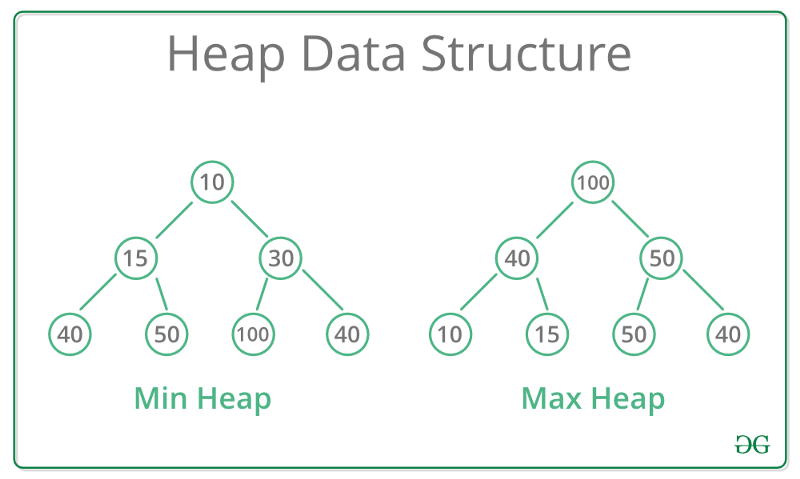
圖片來源:heap-data-structure

關於Heap Tree的實作會在之後的Heap Sort文章中介紹

參考資料: understanding-binary-search-trees

full-binary-tree