在認識動態規劃之前先來理解Divide and Conquer(分治法)吧!Divide and Conquer是一種演算法，執行的步驟如下

1. Divide:先將大問題不斷切割成小問題
2. Conquer:用遞迴的方式處理所有的子問題
3. Combine:將所有的結果合併起來就是最終解答

動態規劃的概念與Divide and Conquer的概念相似，會將大問題切割成多個小問題，再將小問題的解答組合起來，不過有些小問題其實是重複的，所以會發生重複計算的問題，這時候動態規劃就會把已經計算過的答案存起來，用空間換取時間，加速執行時間，這就是動態規劃的核心精神所在。

斐波那契數列

斐波那契數列由0和1開始，之後的斐波那契數列就是由前兩位數字相加而得出 ，也就是第n項為第n-1和第n-2項的總和 - 引用自wikipedia

圖片來源:https://www.mathsisfun.com/numbers/fibonacci-sequence.html
ex. 89 = 55+34 (n11 = n10 + n9)

下圖是斐波那契數列遞迴執行的流程圖，每個方格都是一個函式，觀察下圖就會發現有不少重複計算的現象，因此時間複雜度為O(2ⁿ)。

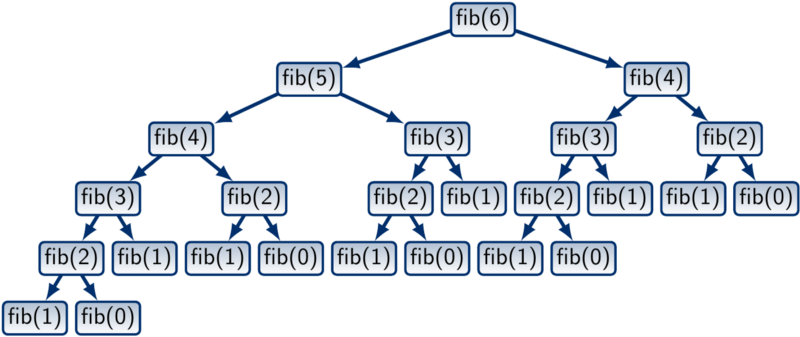
圖片來源:https://tarjotin.cs.aalto.fi/CS-A1140/2020/notes/dynprog-dp.html

用js實作如下

const fibonacci = (i) => {
    if (i === 0 || i === 1) return i;
    return fibonacci(i - 1) + fibonacci(i - 2);
};

fibonacci(5);

而下圖是Dynamic Programming執行的流程，因為藍色區塊已經計算過，並將計算結果暫存起來，所以黃色的區塊不需要重複計算，時間複雜度為O(n)。

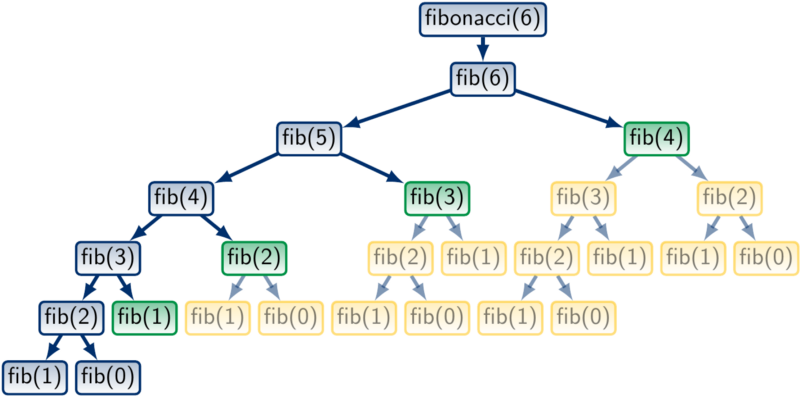
圖片來源:https://tarjotin.cs.aalto.fi/CS-A1140/2020/notes/dynprog-dp.html

為甚麼稱為動態規劃?

因為宣告存放計算結果的陣列長度是隨著輸入的長度變化，存放的方式又分為兩種 Bottom Up和Top Down

• Bottom Up : 使用迴圈，執行順序是由下至上，又稱為Tabulation，可以想成是從小的問題開始計算，逐步計算到最終要求的值，缺點是可能會計算到沒有用到的子問題。

• Top Down : 使用遞迴，執行順序是由上至下，計算過的結果會存起來不會重複計算，這個方法也被稱作memoization，由於遞迴的執行效率相較於迴圈會來的差，因此這種方法會比Bottom Up還要慢，可能會有遞迴過深的問題。

用js實作Bottom Up

const fibonacci = (n) => {
    let temp = new Array(n);
    temp[0] = 0;
    temp[1] = 1;
    for (let i = 2; i < n; i++) {
      temp[i] = temp[i-1] + temp[i-2];
    }
    return temp[n-1] + temp[n-2]
  }

  fibonacci(6);//輸出8

用js實作Top Down

const fibonacci = (n) => {
    return helper(n, new Array(n));
};
const helper = (i, temp) => {
    if (i === 0 || i === 1) {
        return i;
    }
    if (!temp[i]) {
        temp[i] = helper(i - 1, temp) + helper(i - 2, temp);
    }
    return temp[i];
};

fibonacci(6); //輸出8

兩者的差異比較如下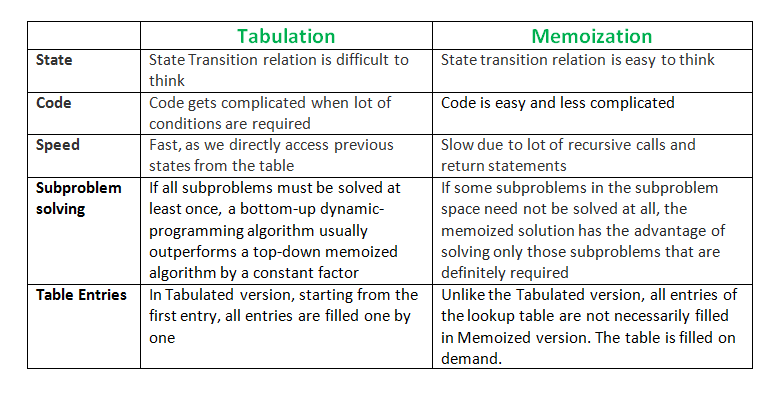

圖片來源:https://www.geeksforgeeks.org/tabulation-vs-memoization/

動態規劃適用的情境

1. 最佳子結構 (Optimal Substructure):問題的最佳解可以從子問題的最佳解推算出來。
2. 重疊子問題 (Overlapping Sub-problems):如斐波那契數列出現重複子問題的情形，動態規劃的優勢是可以儲存過計算過的結果，再次遇到相同子問題的時候直接取出儲存的結果，無需重複計算。
3. 無後效性(no aftereffect):即子問題的解一旦確定，就不再改變，不受在這之後、包含它的更大的問題的求解決策影響。

參考資料:dynamic-programming-laughlin-lunch-and-learn
tabulation-vs-memoization
Overlapping Subproblems Property in Dynamic Programming
动态规划