The dream of every cell is to become two cells.
-- François Jacob
Previously:
or, center the pink cell,
We finished the red-pink face, and with two more pink cubies we finished the pink-green face as well. Now 6 out of 16 cubies are done, which is 37.5% finished.
To tell the truth, I think so far we have been very lucky. I don't remember if we ever encounter orientation problems. All the orientations we have done in the past few days are fairly intuitive (after spending some time staring at the puzzle, of course). But now I don't think it will always be that smooth.
The rest two pink cubies are at Z+O1 (orange-pink-gray-blue, by deduction) and Y+O4 (yellow-pink-gray-orange). The former should go to W-O6 and the later should go to W-O7. If you feel a little bit weird about the situation, then you are sharp. Yes, Y+O4 and W-07 are actually two stickers that belong to the same cubie. The cubie is already there, the place it should be, but it doesn't look right, because the orientation is wrong. The yellow at X+O6 is the only correct one, but its rest three stinkers are mis-placed.
There is no way to change a cubie's orientation without moving it to other places first, at least not possible in 2x2x2x2. The strategy I can think of, is to move it away from the pick cell, do some twist so that its orientation is convenient there, and then join it with other pink cubies.

Seperate it from the cell first. I choose to Z-axis-twist the Z+ so that the Z+ side 4-pink cluster goes to X-, and then Z-axis-twist Z- in the opposite direction. Final setup step is to Y-axis-twist X- so that the 6 previous-done pink cubies are at the W+ side of the puzzle. In other words, the 7th cubie is free in W-.
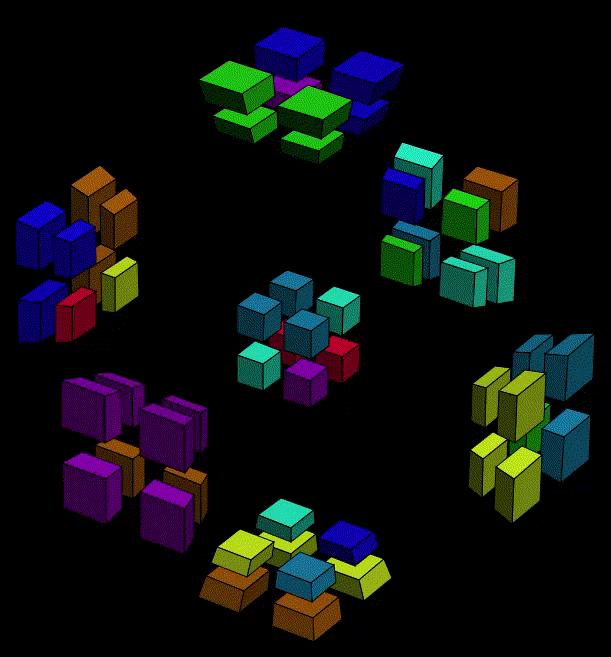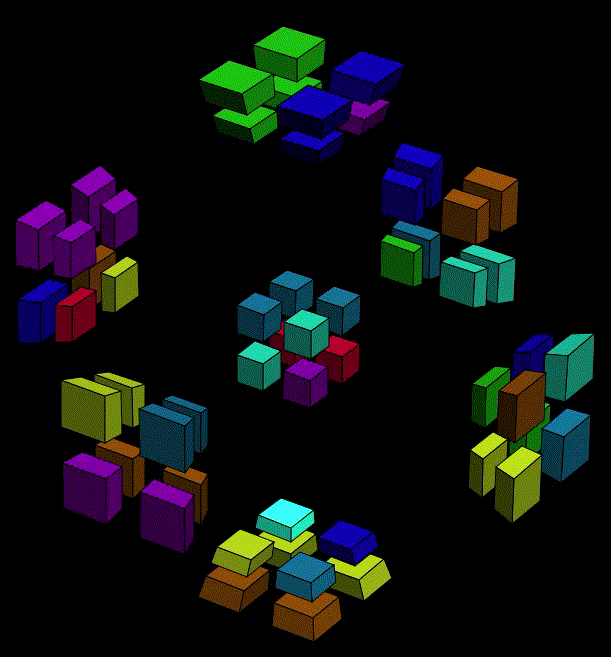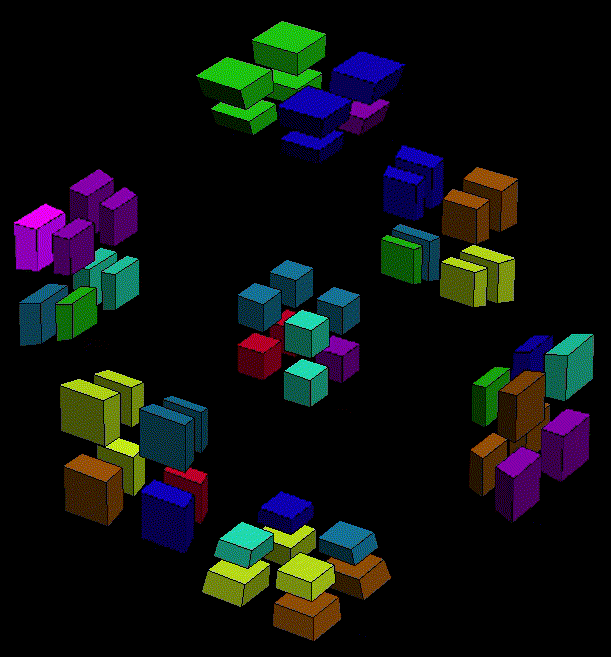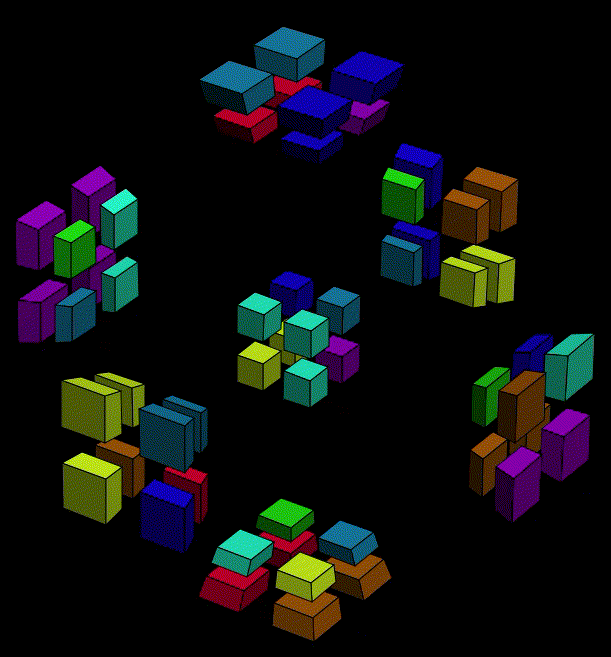
Similar to the appraoch we executed yesterday, we should consider the "return" of a new cubie in to halves. The first is often mysterious and hard to figure out where to start, but we know that roughly we should create a situation that key cubies are free so that we can adjust its orientation while make sure the setup of existing cluster is inverseable. The second half is more imaginable. Assume that we have a new cubie out there waiting to join its fellow cubies, and the cluster is like it is intact from the beginning. The second half is some simple twist sequence that the new cubie can eaasily return.
If the cubie's pink was at W-O0, then twe can do a clockwise X-axis-twist to Z-, pushing the Z- side of the pink cluster to W-. Then a clockwise Y-axis-twist brings W-O0 to W-O7. It would be convenient if at this moment, X+O6 is yellow, Y+O4 is gray, and Z-O0 is orange. Then when the counterclockwise X-axis-twist to Z-, the 3-pink cluster is shifted back to Y-, and the 7th cubie is done.
It's hard to expain now, because I just found this sequence that makes the 7th cubie goes to W-O1 while the 4-pink cluster goes back to Y-. The goodthing about this sequence is, later when the Y+ side of the puzzle is free to move, we can apply Y-axis-twist to Y+, and as the pink sticker goes back to W-O7, the other colors are all settled in a right orientation.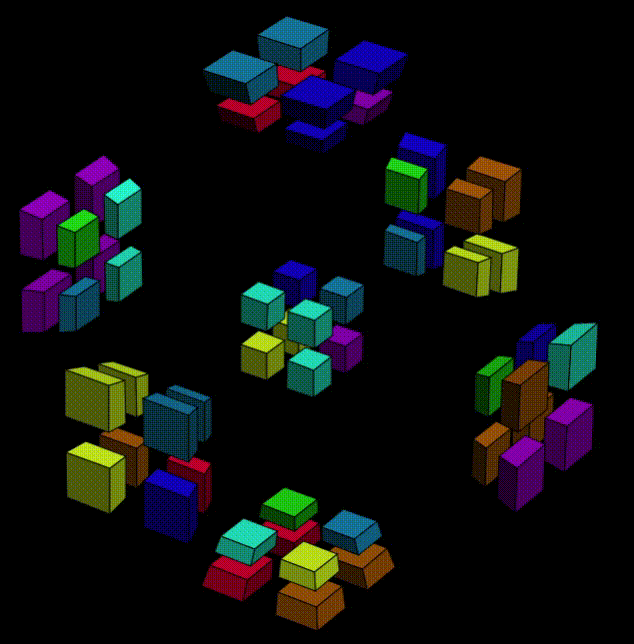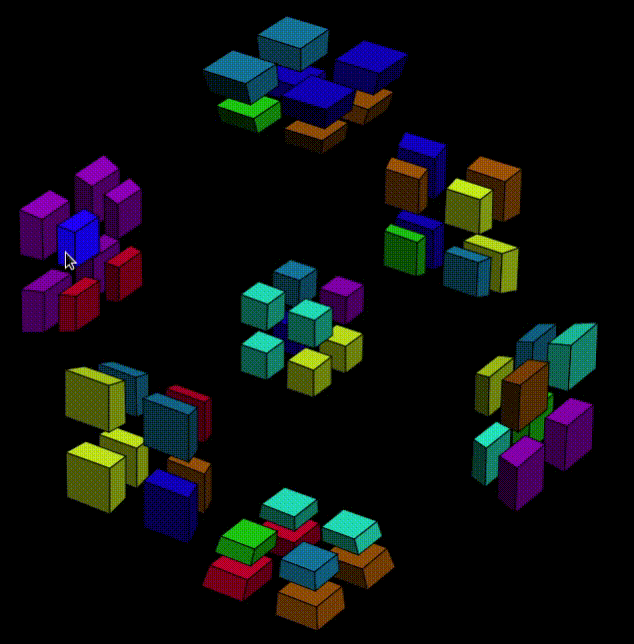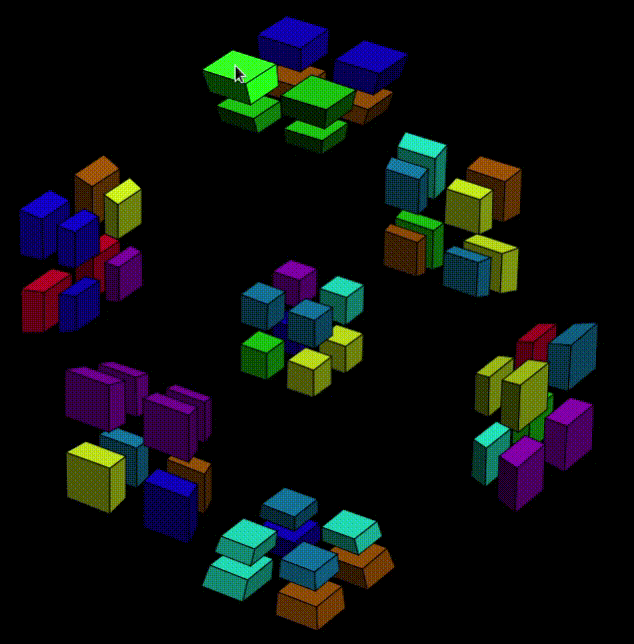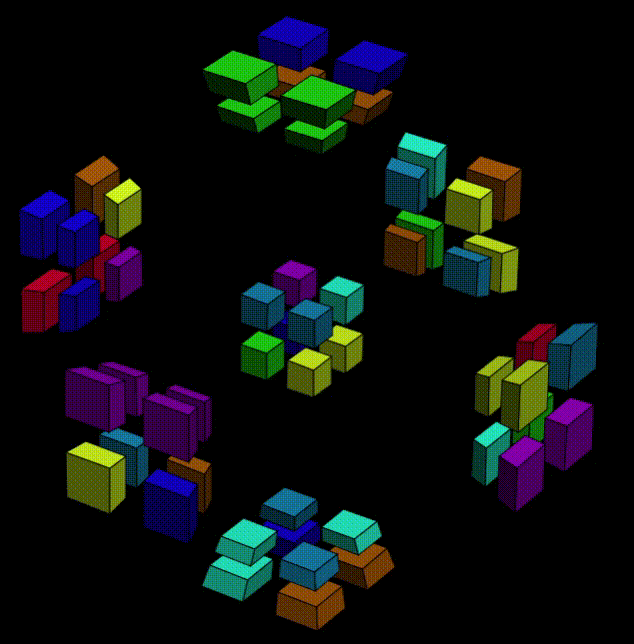
So the rest is simple, described above as
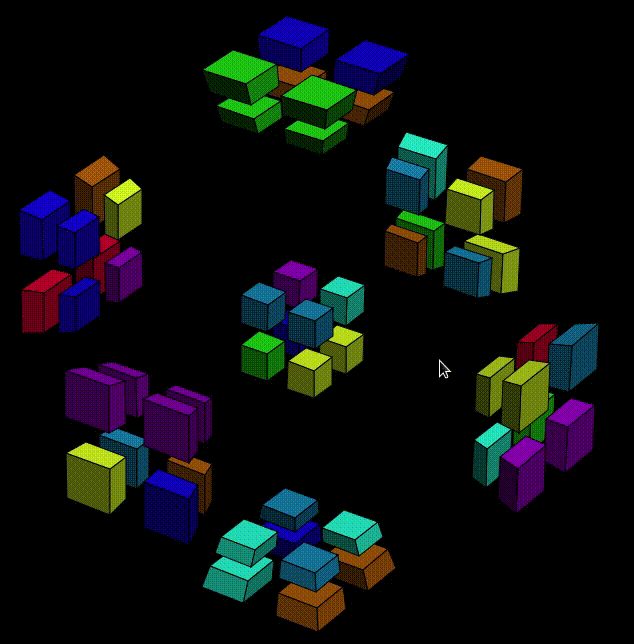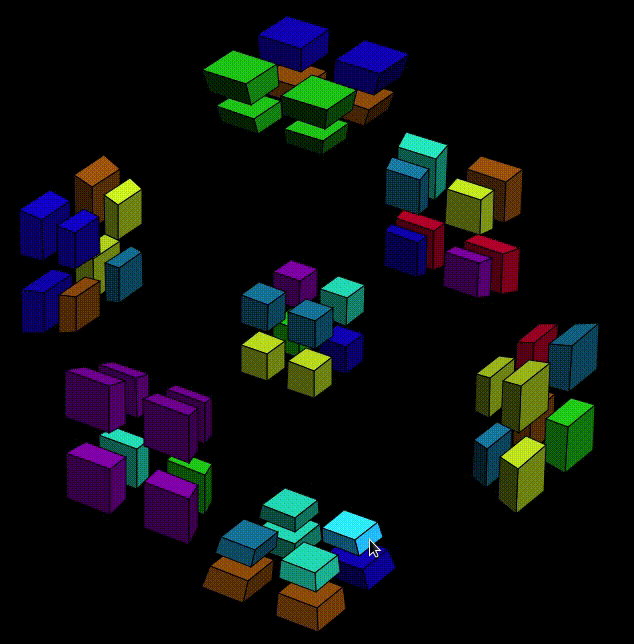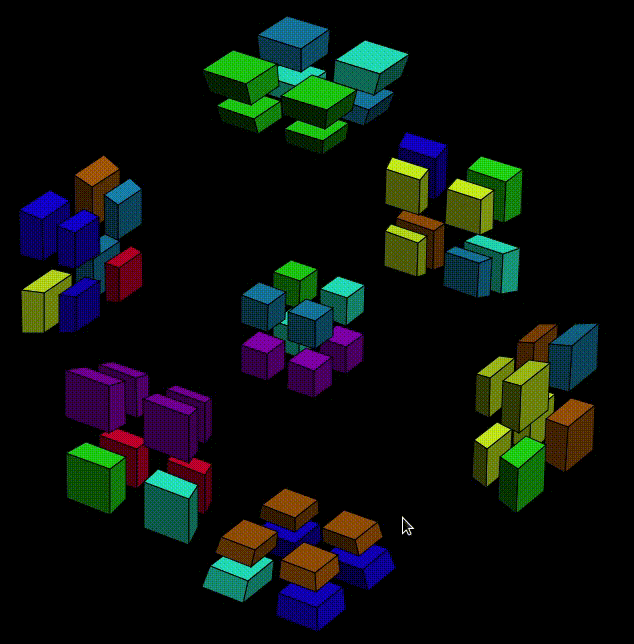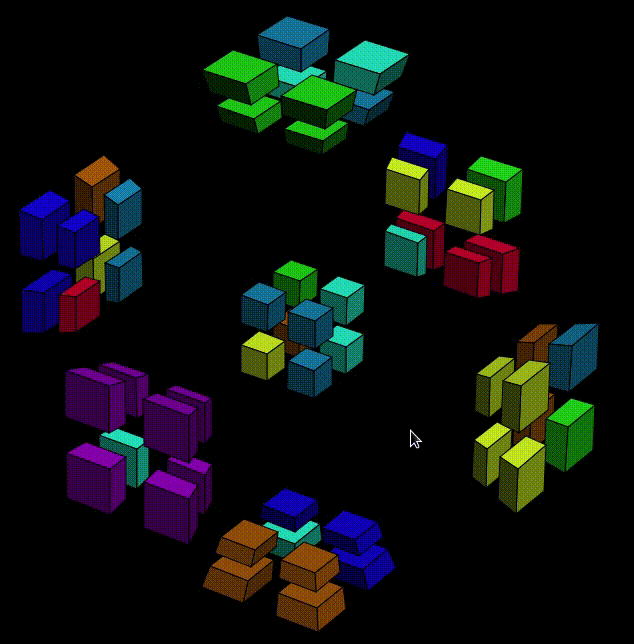
Why is my pointer suddenly visible? Thanks to the great software SimpleScreenRecorder.

Although we cannot see the 8th pink sticker directly, it must be a blue-pink-orange-gray cubie. By deduction (or by centering cells to see them), the Y-O1 reveals its true identity. But even if I can tell this in less than a minute...
For the rest 1 hour, I tweak this a that, try some twist combinations, but still nothing really works. Given the fact that we have a 7-cluster, It become impossible for me to intuitively deal with the oriention and freedom and position of the cubie(s) altogether. I cannot event think of a viable second half, the recovering sequence given every setup is OK.
So far, our second half attempts are similar to each other: some twists that detatch some part of an established cluster, a twist that send a sicker from another cell to W- at the right position, and then inverse the first twist. Y- cell plus one finished cubie. It is not the only way to do this. Imagine this: the 8th cubie is at the Z+ side of W-, a cluster comes to the Z- side of W-, and then some Y-axis-twists to the Y+, which remian the orientation (on W- and Z+) but still effectively merge the cubie into the Z- of W- with the cluster.
It should be possible. Our 7th was put in its correct position, but if it was put in Z-O6, then we can set the 8th cubie at W-O1 with the right orientation, then execute the above plan, the the Z- side of Y- should be done, which is our first cell.
OK, it is rather easy to move the 7th to where 8th should be, as follows,
Note that our target 8th cubie is now at X+O0a. Ideally, if we can make its pink sticker at W-O1, gray sticker at Y+O2, orange sticker at X-O0, and blue sticker at Z+O6, then after we execute the above plan, everything will be perfect. The problem now is how.
Let's put the pink sticker back in our sight first,
Fast forward another 30 minutes, I did this,
To be honest, my intuition cannot carry me forward anymore, so I try to develop a algorithm to change the desired cubie's orientation. For those experienced readers, you may know some theoretical approach like commutator or condugate. My method is not as fancy as those.
The idea is simple. If I break a cubie group apart and then glue them back together, there might be some change to the other part of the puzzle. For example, maybe cubie A was at place B, after the sequence of twists, cubie A goes to placce C and cubie D comes to place B. We can reasonably say that, if we perform the identical sequence again, cubie D will go to place C. Maybe coincidentally, cubie A goes back to place B at the same time. If this is the case, there is a place B->C->B cycle, or we can say the sequence is a 2-cycle algorithm.
With this break-and-glue method, you have to try a few times to see what works and what not. Let's choose Y-O1 as the cubie to be break-and-glue'd, and perform the following,
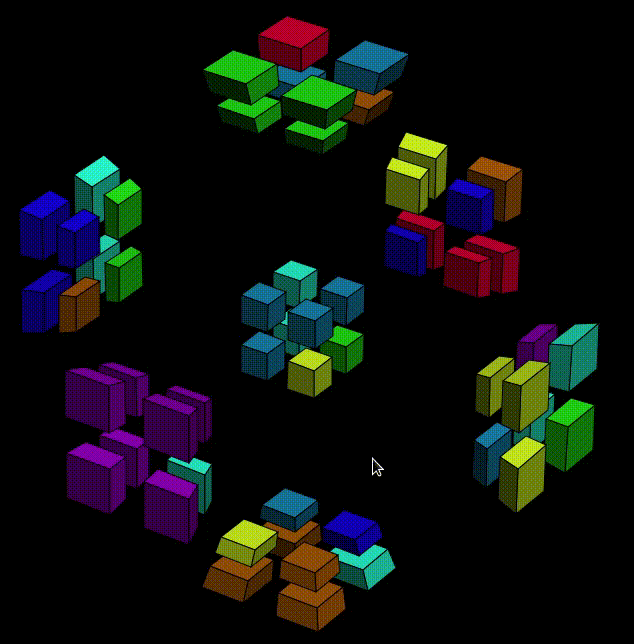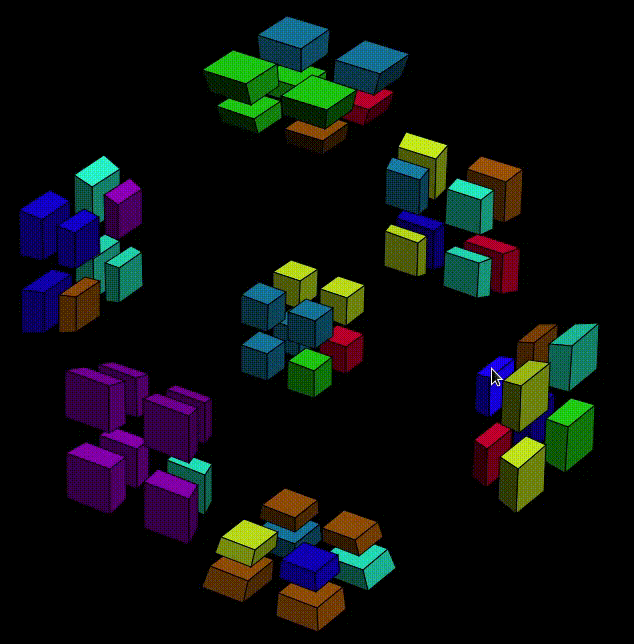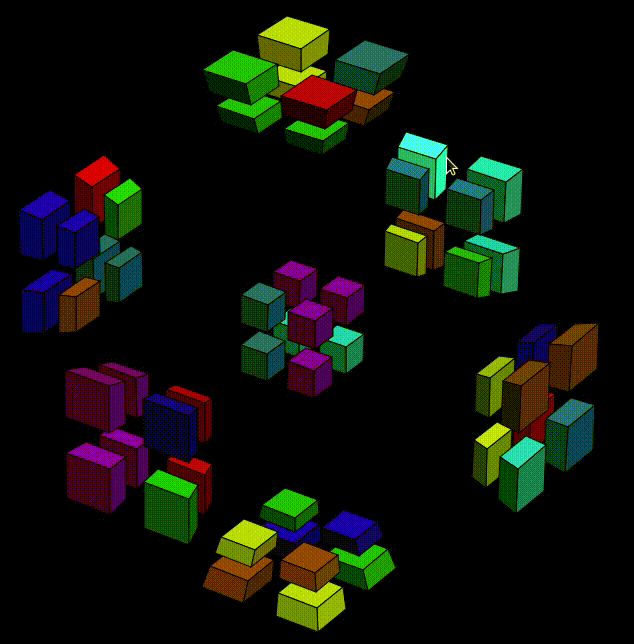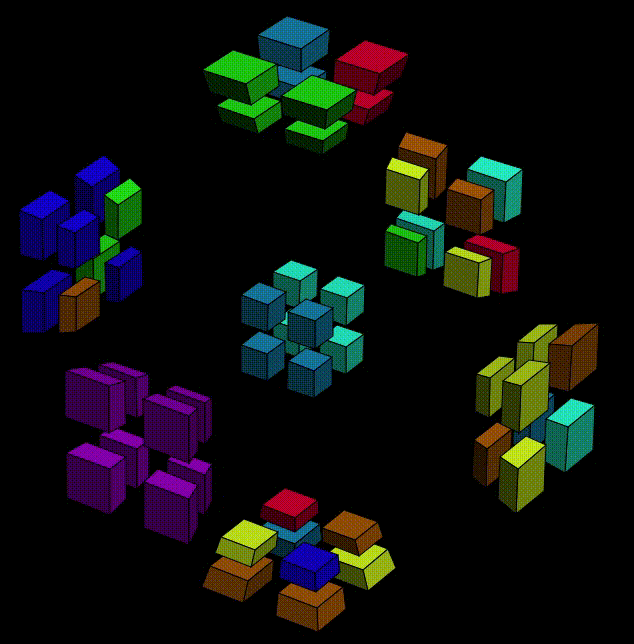
Wait, what? Are we finished? No. Don't be fooled by the all-pink cell. We move Y-O7 to Y-O6 on purpose, remember? So Y- is actually becoming more difficult to deal with: two cubies are in the wrong place, but still in the same cell. Let's rewind, and find some other condition that works. We already know that we shouldn't put the pink sticker at X+O1, so this time let's try X+O6,
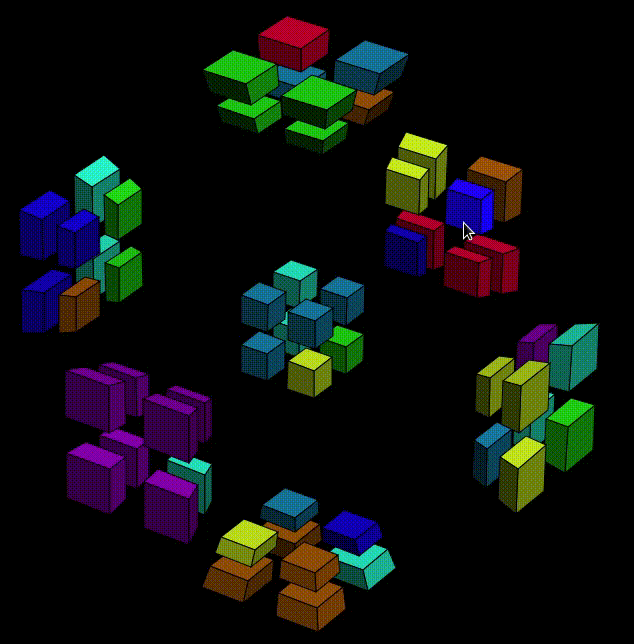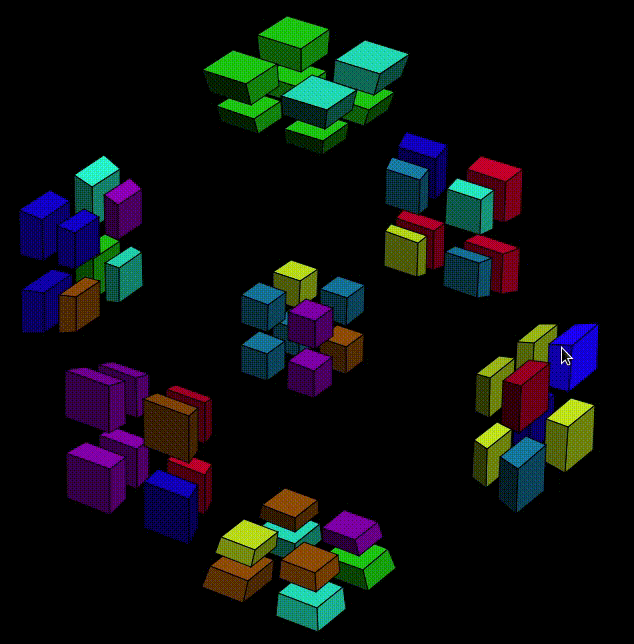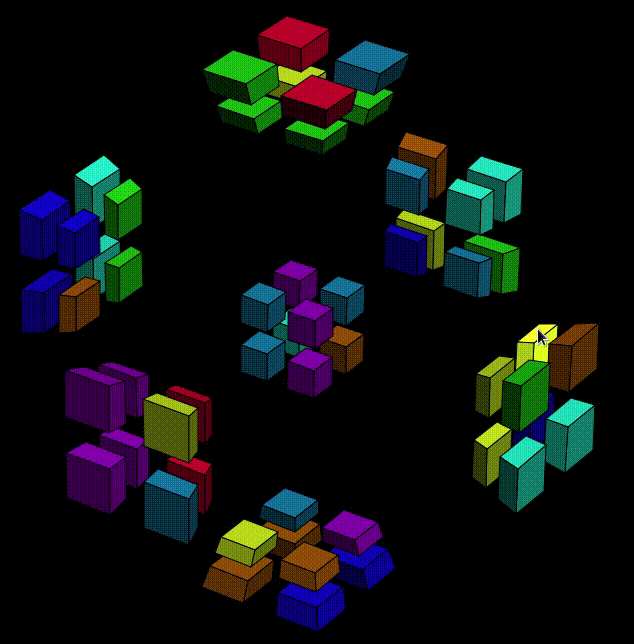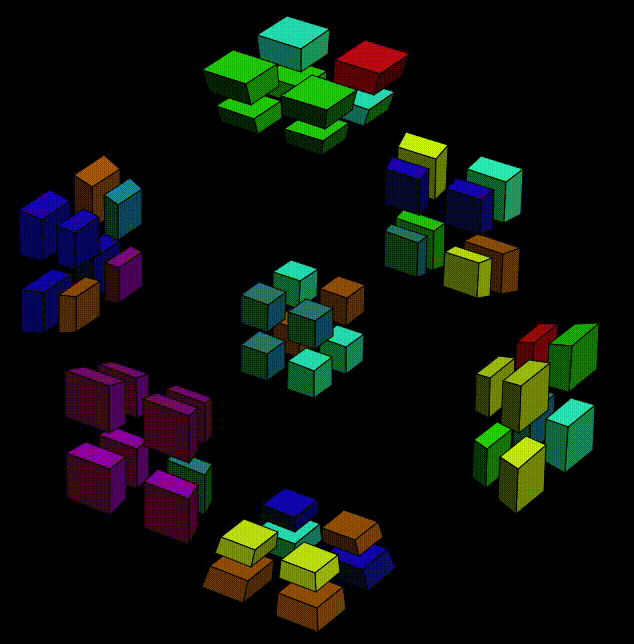
Now some interesting thing happened. Originally, the pink sticker was at X+O1, and the X-Y-Z-W stickers were pink-blue-orange-gray. Now, the pink sticker is at X-O7, its orientation becomes pink-gray-blue-orange, which is equivealent (after a clockwise Y-axis-twist to Y+) to pink at Z+O6 with orientation blue-gray-pink-orange.
Our ideal orientation is orange-gray-blue-pink, which means that if we can setup blue-orange-pink-gray with pink at Z-O0, after the algorithm, it will be ideal for the second half twists.
Wait, but the free cell is Y+ and the Y+ now is gray, so with a easy combination of two twist, we can shift the pink sticker to W-,
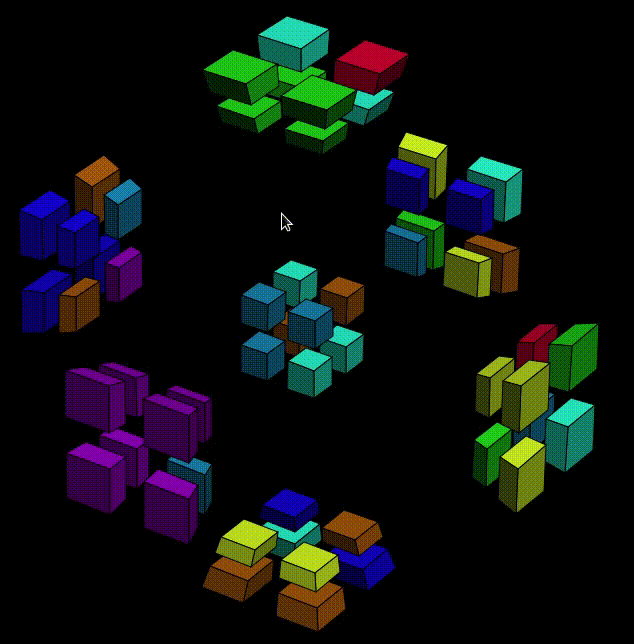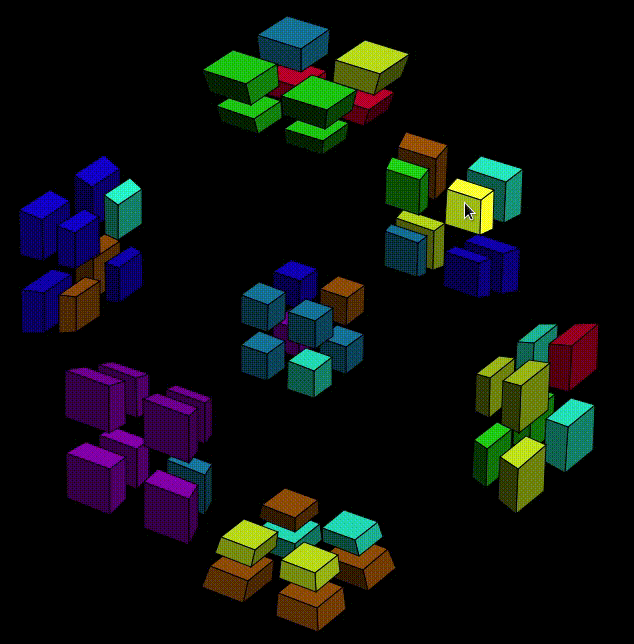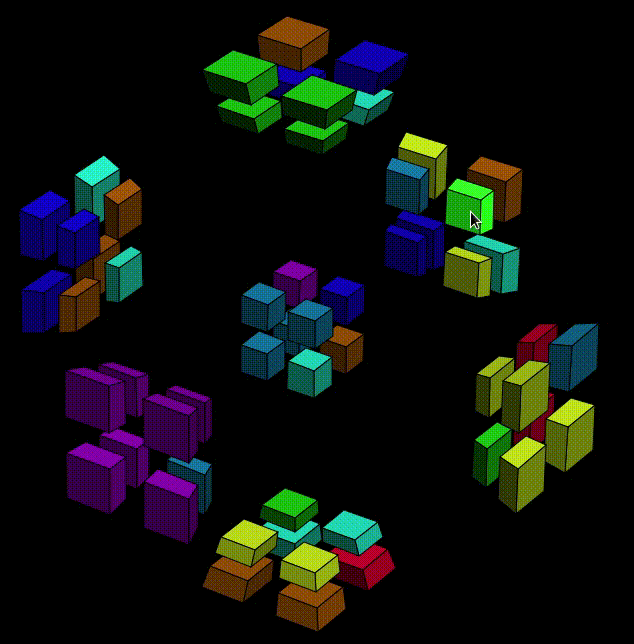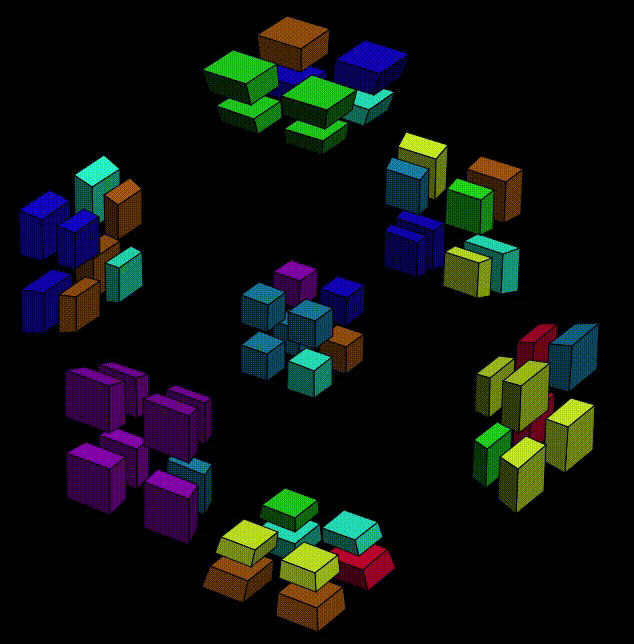
OK, then now we can execute the second half,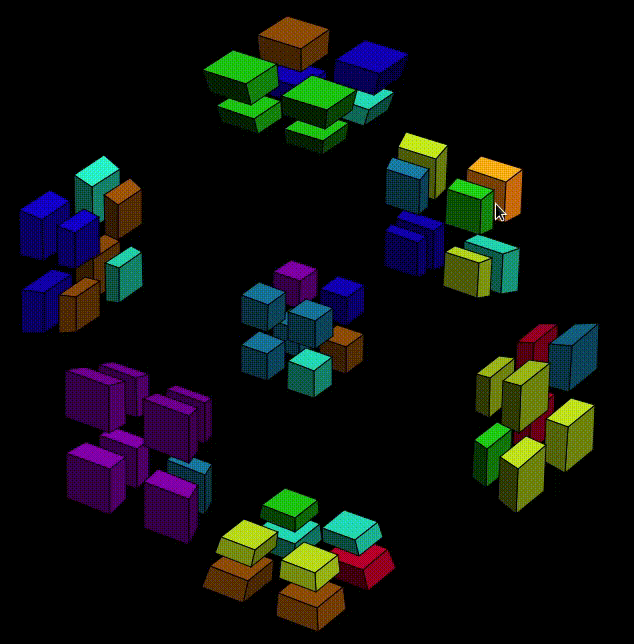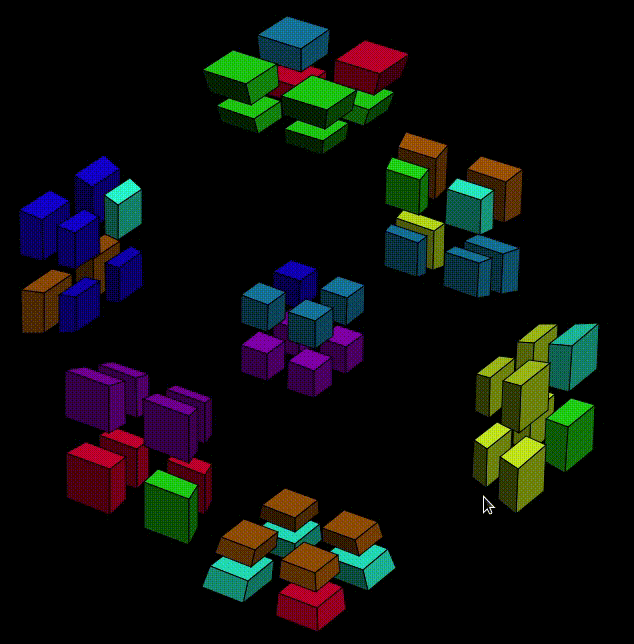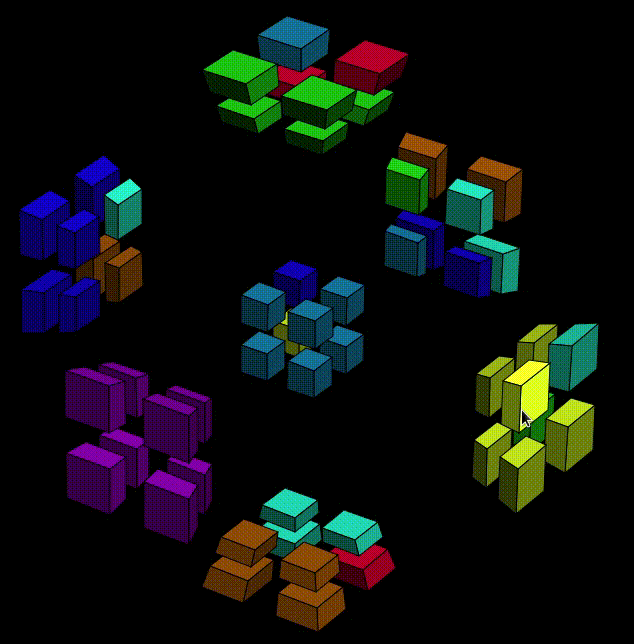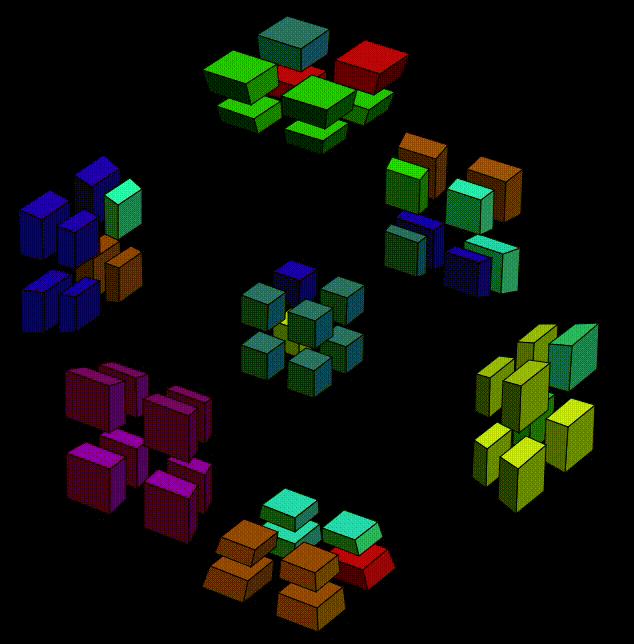
That's it!!! Our! First! Cell!
The last two pink stickers are not easy. We can handle the 7th by intuition, but not for 8th. Our first algorithm is developed but it does not has great use for our later challenges. Anyway, we will see.
完成了 2x2x2x2 的第一個胞。
