本單元將進入影像雜訊分析。一個影像的雜訊也有很多種類，每種都有不同的特性可以做處理，既然如此，要進行什麼處理?當然是還原囉，我們不希望看到的影像是失真的、有雜訊的，因此影像還原的技術，有助於我們重建原始影像。

1.影像還原基本概念

影像還原(Image Restoration)可以定義為:「基於事先已知的失真現象對數位影像進行還原的技術」。

影像失真與還原模型，如下圖所示。影像還原技術，通常需事先了解造成影像失真的原因，才能進行處理，還原成原始的數位影像。因此，在討論影像還原技術時，也要一併了解**影像失身(Image Degradation)**部分。

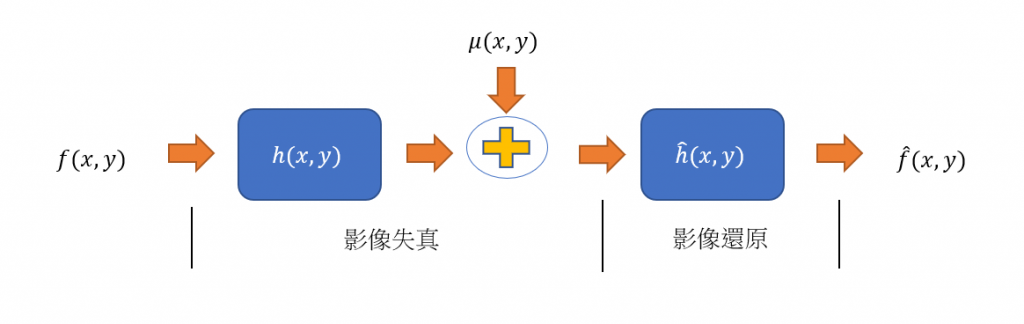
影像失真的模型可定義為:
![https://ithelp.ithome.com.tw/upload/images/20220919/20152370DZ01C6cO5c.png](https://ithelp.ithome.com.tw/upload/images/20220919/20152370DZ01C6cO5c.png)
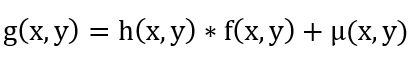
其中，h(x,y)為失真函數;u(x,y)為雜訊;星號為卷積運算，影像還原的目的是希望輸入失真的數位影像g(x,y)，經過逆過程產生輸出數位影像f`(x,y)，可以還原原始的數位影像，也就是f`(x,y)~=f(x,y)。

2.影像雜訊

最簡單的影像失真模型，就是在數位影像中加入雜訊(Noise)，稱為**影像雜訊模型**，定義如下:

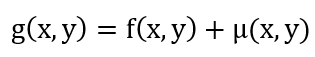
其中f與g分別為輸入與輸出的影像;u稱為雜訊。

雜訊可以採用數學模型的方式來定義，主要根據機率密度函數(Probability Density Function,PDF)定義。假設機率密度函數是定義為p(z)，則必須滿足: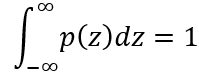

也就是機率的總和為1(或100%)。

典型的雜訊模型有以下幾種:

• 均勻雜訊(Uniform Noise):均勻雜訊的PDF可以定義為: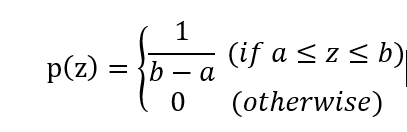
  
  因此，PDF曲線下的面積為1。實際應用時，假設a = 0,b=scale，參數scale可以決定均勻雜訊的強度

• 高斯雜訊(Gaussian Noise):又稱為常態分佈雜訊(Normal Distribution Noise)，其PDF就是高斯函數: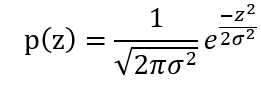
  
  其中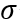
  為標準差，實際應用可以假設 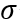= scale，可用來決定高斯雜訊的強度。

• 指數雜訊(Exponential Noise):指數雜訊的分布呈指數衰減，其PDF是根據指數函數的定義: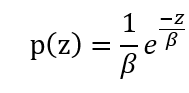
  
  其中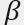=scale，可用來決定指數雜訊的強度