現實生活空間中，通常會存在某種程度的雜訊。影像處理系統在擷取或傳輸影像的過程中，通常會受到雜訊干擾，因此可以對影像雜訊進行分析，並採取對應措施，改善影像處理系統的效能

1.訊號雜訊比

影像雜訊分析，最典型的方法就是 訊號雜訊比(Signal-to-Noise Ratio) ，源自於數位訊號處理技術。

假設無雜訊的數位影像為f(x,y)，失真的數位影像為f`(x,y)，可定義下列的量化評估依據:

• 總誤差(Total Error) 為誤差的總和，可以定義為: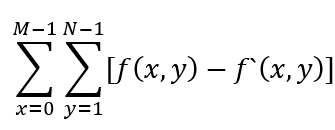
  
  由於誤差分成正誤差與負誤差兩種，上述的評估方式可能會產生相互抵消的結果，故不長用。

• 均方誤差(Mean-Square Error,MSE) 定義如下: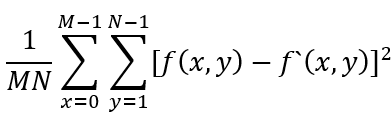
  

• 均方根誤差(Root-Mean-Square Error,RMSE) 定義如下: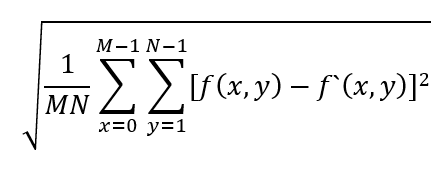
  

• 峰值雜訊比(Peak Signal-to-Noise Ratio) 定義如下: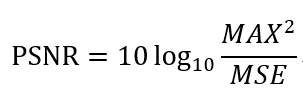
  
  其中，MAX為最大值(以數位影像來說，255為最大值)，MSE是上面提到的均方誤差。

  數位影像處理領域中，PSNR是雜訊分析時理想的量化評估工具，因此經常被用來在數位影像處理或傳輸系統的效能評估。若PSNR值越高，表示失真的數位影像品質越接近原始的數位影像。若PSNR高於30dB，通常被視為是理想的影像品質，反之若低於20dB，則被視為影像品質較差的失真影像。

  假設在原始的數位影像加入高斯雜訊，標準差為20，計算PSNR值，程式碼如下:

import numpy as np
import cv2
from numpy.random import normal

def gaussian_noise(f, scale):
    g = f.copy()
    nr, nc = f.shape[:2]
    for x in range(nr):
        for y in range(nc):
            value = f[x, y] + normal(0, scale)
            g[x, y] = np.uint8(np.clip(value, 0, 255))
    
    return g

def PSNR(f, g):
    nr, nc = f.shape[:2]
    MSE = 0.0
    for x in range(nr):
        for y in range(nc):
            MSE += (float(f[x, y]) - float(g[x, y]))** 2
    MSE /= (nr * nc)
    PSNR = 10 * np.log10((255 * 255) / MSE)
    return PSNR

def main():
    f = cv2.imread("D:\Desktop\IThome\lena.bmp", 0)
    g = gaussian_noise(f, 20)
    print("PSNR = ",PSNR(f, g))
    cv2.imshow("Original", f)
    cv2.imshow("Gaussian Noise", g)
    cv2.waitKey()

main()

上述程式碼為產生一個亂數標準差分別為10、20、50，並計算PSNR值。結果如下: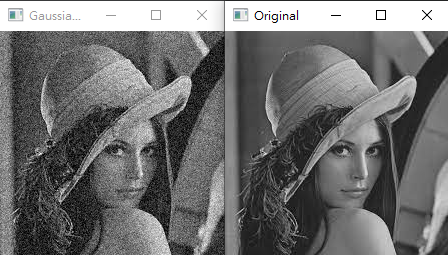

2.影像雜訊分析

假設我們取得一張含有雜訊的數位影像，可以透過簡易的雜訊分析，理解影像雜訊的特性與本質。理解影像的雜訊與本質。而雜訊具有隨機性，因此可以考慮使用雜訊模型進行模擬分析。

程式碼如下:

import numpy as np
import cv2
import matplotlib.pyplot as plt

def histogram(f):
    if f.ndim != 3:
        hist = cv2.calHist([f], [0], None, [256], [0,256])
        plt.plot(hist)
    else:
        color = ('b', 'g', 'r')
        for i, col in enumerate(color):
            hist = cv2.calcHist(f, [i], None, [256], [0,256])
            plt.plot(hist, color = col)
    plt.xlim([0, 256])
    plt.xlabel("Intensity")
    plt.ylabel("#Intensities")
    plt.show()

f = cv2.imread("D:\Desktop\IThome\lena.bmp",0)
ROI = f[55:95, 55:95]
histogram(ROI)
print("Sigma = ", np.std(ROI))

此程式碼，首先擷取數位影像中的ROI(平坦區域)，並呼叫函式，顯示直方圖，Python的Numpy的套件提供std函式，可以用來計算ROI內像素的標準差。

相對而言，取得局部區域的雜訊具有規律性，則鷹派段為周期性雜訊，此時可透過頻譜分析，並評估雜訊在頻譜中宇中心的距離，藉此判斷雜訊的相關參數。