前言

教學Deap之概念之前，還是強烈建議先去看第(04)篇，把二元樹的定理搞懂，才較能理解以下內容喔

定義

1. 為 Complete Tree
2. root is empty
3. 左樹為 min heap
4. 右樹為 max heap
5. 對於左樹某點 i 相對應在右樹位置為 j

How to calculate relativ j ?

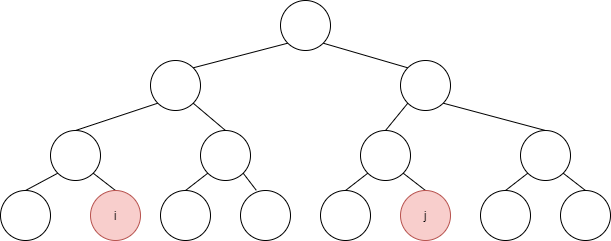
已知為 complete BT，儲存在 Array 之中時，每個節點是依照順序排好的，因此在左 Heap 之某點 i，在右 Heap 則擁有相對應的 j 點，觀察此 Deap，可以發現 **j = i + 上層之最多Node 數 **，因此我們可以來推公式啦！

上層最多 Node 數如何計算？

首先，之前談過如何利用節點總數去推出最小樹高，我們先利用
得出到 i 點時的最小樹高，因此上一層的樹高即為
以上一層來看，利用葉求最小樹高的公式反推
就可以知道 i 上一層之最多節點個數囉
只要將最多節點個數加上 i 即為 j，

操作

Insert x

// CASE 1 若為插入左子樹，也就是新點在min heap
if(x > deap[j]){ // 若插入元素右子樹相對應j還要大
    deap[n] = deap[j]; // 將j之元素換到左子樹
    insert_max_heap(deap,j,x); // 將x依照max_heap之插入操作，插入右子樹j之位置
}else{ // 若較小則x仍在左子樹
    insert_max_heap(deap,n,x); // 將x依照min_heap之插入操作，插入最後位置 
}

// CASE 2  若為插入右子樹，也就是新點在max heap中
if(x < deap[j]){
	deap[n] = deap[j];
	insert_min_heap(deap,j,x);
}esle{
	insert_max_heap(deap,n,x);
}

delete min

1. 先刪除最小點 (位於左子樹之 Root)
2. 移除 the last node 令其為 X
3. 先將 min heap 由上到下調整直到 leaf 有空樹葉

針對該位置(空樹葉)進行 Deap 之 insert X