資訊理論中，熵編碼(Entropy Coding)是一種無失真壓縮技術，可以用來對不同的多媒體資料進行壓縮，而在解壓縮時可以保證原始資料的重現。熵編碼的目的，希望可以達到接近熵的理想資料壓縮比。

典型的熵編碼技術包含以下兩種:

• 霍夫曼編碼(Huffman Coding)
• 算術編碼(Arithmetic Coding)

霍夫曼編碼

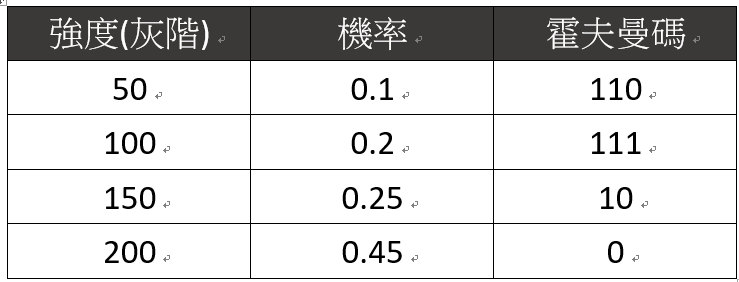
霍夫曼編碼技術是由美國電腦科學家**大衛．霍夫曼(David Huffman)於1952年發行的編碼技術，目前被廣泛應用於許多資料壓縮標準。霍夫曼編碼的原理是先對準被壓縮的資料進行機率分析，對於發生機率較高的資料，以較短的位元串(Bit Strings)**表示;對於發生機率較低的資料，則以較長的位元串表示。

假設給定一張500 x 500 的數位影像，影像中僅包含4種強度(灰階)，分別為:50、100、150、200。強度的機率分佈與兩種不同的編碼方式:(1)固定長度編碼;與(2)可變長度編碼如下表: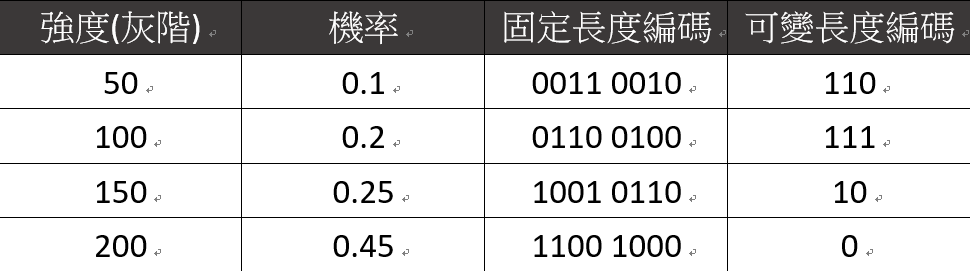

若採用固定長度編碼，原始影像中每個像素使用8為元儲存，則無壓縮的數位影像所需的總資料量為: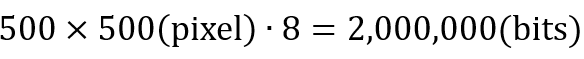

若採用可變長度編碼，或稱為霍夫曼碼，則每個像素平均使用的位元數為: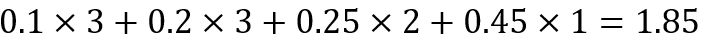

因此若採用霍夫曼編碼技術，壓縮後的數位影像所需的總資料量為: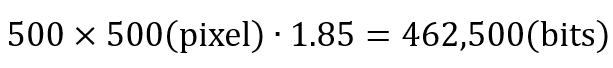

壓縮比為:

那我們再來進算這個數位影像的熵: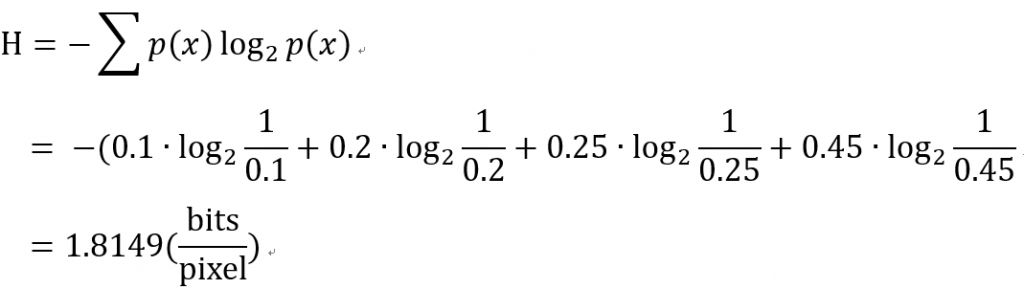

若予以上像素的平均位元數比較，可以發現霍夫曼編碼的果，非常接近計算的熵。也就是說，霍夫曼編碼可以提供理想的資料壓縮，相當接近無失真壓縮的極限。

若觀察本範例的霍夫曼碼，可以發現任何一個字碼(Codeword)，均不是其他字碼的前置碼，因此，霍夫曼碼是典型的前置碼(Prefix Codes)。前置碼的優點為:傳送端可以直接連接與傳遞訊息，接收端也可以及時進行解碼。

例如:給定一個編碼後的0與1序列:011110110，可以進行即時解碼: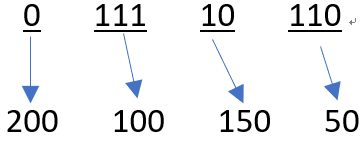

霍夫曼編碼技術，使用的演算法為貪婪演算法(Greedy Algorithms)，是電腦科學中相當重要的演算法。資料壓縮演算法中以霍夫曼編碼最具代表性，被廣泛應用於許多壓縮標準，例如:MP3、JEPG、MPEG等。

霍夫曼編碼的演算法如下:

1. 首先，輸入**源符號(Source Symbols)與發生機率。根據輸入的符號與發生機率，建立節點(Node)**序列。
2. 取出最小機率與次小機率的節點，將兩者相加建立新節點。
3. 將新節點插入原來的序列，並重複步驟2。
4. 建立霍夫曼樹(Huffman Tree)，按照左0右1的原則編碼，節點的走法順序就是霍夫曼碼。

讓我們來練習一下，假設有以下強度的灰階與機率: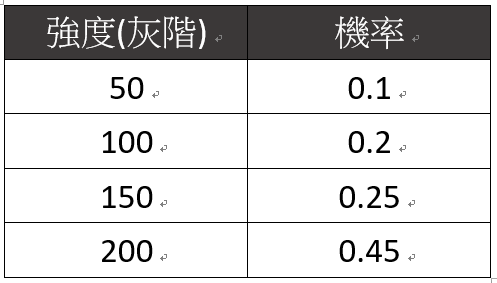

一開始，先建立四個節點的序列，如下圖:

接著將0.1和0.2取出，相加合併0.3，放入原序列。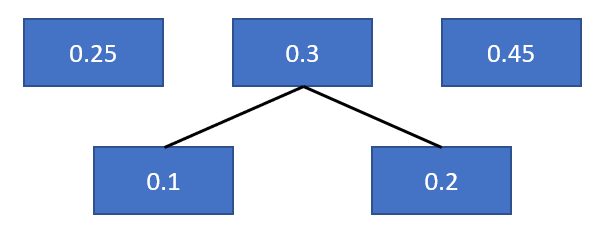

接著一直重複步驟，直到序列為空，然後按照左0右1製作霍夫曼樹。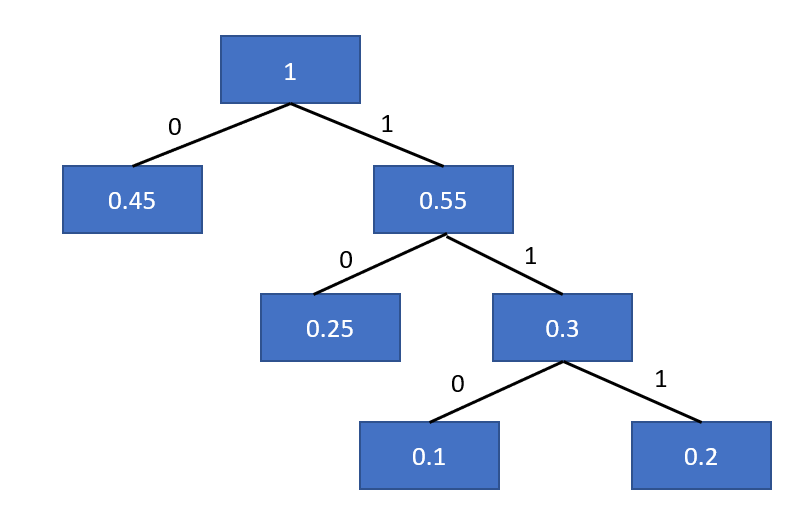

節點的走訪順序就是霍夫曼編碼: