本章節將進入一個很有趣的技術-資料壓縮(Data Compression)。

1.資料壓縮基本概念

什麼是資料壓縮呢?簡單來說，就是把「不必要的或多於的資訊去除、保留重要資訊，藉以節省資料量」的技術，其實生活中也有很常見的例子，例如National Taiwan University可以簡寫成NTU，當我們看到前者或是後者，我們都知道它們都代表國立台灣大學，這就是一個現實中資料壓縮的例子。

而在現今的電腦科技中，資料壓縮的技術也十分常見，例如:zip檔案，或是youtube的vp9、av1編碼等都是資料壓縮的應用。資料壓縮的目的，是希望用較少的資料量(或bit數)表示相同資訊，不僅可以在傳輸時節省頻寬的需求與傳輸時間，儲存時也可以節省硬體。

目前資料壓縮技術可以分成兩類:

• 無失真壓縮(Lossless Compression):資料經過壓縮後，再經過解壓縮，可以完全重建原始資料，不會造成任何失真現象。無失真壓縮可以保證資料的完全重建，因此適用於文字檔、可執行檔，例如:zip、rar等等。通常無失真壓縮的效能會比較有限。
• 失真壓縮(Lossy Compression):資料經過壓縮後，無法完全重建，會造成失真現象。失真壓縮的目的是以大幅減少資料量為主要目標，但希望重建後的資料，也可維持一定的品質，使一般人不易察覺，因此被廣泛應用於音樂、影像、視訊等，例如:mp3、jpeg、H.264、H.265、MPEG等等。

2.資訊理論

資訊理論(Information Theory)是一個應用數學與電腦科學的分支，主要由夏農(Shannon)發展，用來找書訊號處理與通訊的基本限制，例如:資料壓縮、資料傳輸等等。

現在想請問讀者一個問題，如果新聞預報說:明天台北會下雨 和 明天台北會下雪，請問哪個帶給你的資訊量比較多? 若明天會下雨，大家都會覺得這是正常現象，帶把傘就好了;但是大家看到明天會下雪，就會要準備例如防寒衣物、糧食，甚至有些人還會去查詢為什麼會下雪、造成台北下雪的原因。

因此，我們可以推斷，當一個發生機率比較低的事件發生時，帶給我們的資訊量是比較多的，反之當一個發生機率較高的事件發生，反而不會帶給我們很多的資訊，因為我們大致上可以預測到這會發生。

藉由這個觀念，我們可以開始推導**自我資訊(Self-Information)**。假設現在有個任意事件x，發生機率為P(x)，那麼，P(x) = 1代表這個事件是100%發生的，那麼這個事件帶給我們的資訊就會很少，而若P(x) = 0.1 代表這個事件一旦發生，那麼帶給我們的資訊就會很多。

那麼，有沒有哪個函數，可以代表上面的數學式呢?，若P(x) = 1，那麼我們可定義自我資訊I(x) = 0，代表沒有帶給我們任何資訊。因此，我們可以取對數的方式，如下:

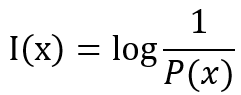
那麼，當P(x) = 1，這個數字就會是0了!，因此這就是自我資訊的定義，但是現實中我們不會只有一個事件，所以我們若把這件事件的自我資訊和它們的發生機率相乘，最後再相加，就會得到: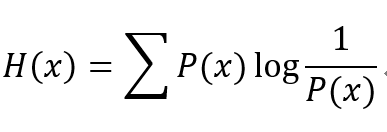

上述的H(X)就是 熵(Entropy)，代表接收的每個事件包含的平均資訊量。這麼部分會比較數學理論一點，但若搞懂這些推倒以及代表意義，對於理解資訊理論是非常有幫助的!

舉例來說，丟一個錢幣、正反面發生的機率各為0.5，那麼:

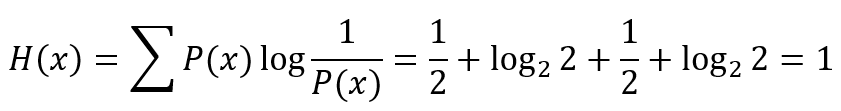
代表著丟一個錢幣的總資訊量為1，我們可以用一個位元來儲存這個結果。