Tree

在第 7 天的文章中，我們介紹了 Tree。

Tree（樹）是一種資料結構，是具有樹狀結構性質的資料集合。

接下來我們要介紹兩種不同類型的樹。

Binary Search Tree

Binary Search Tree，縮寫為BST 是一種常見的資料結構，用於儲存和組織數據。

它是由節點組成的樹狀結構，每個節點都包含一個值，並且具有左子樹和右子樹，這些子樹也是二元搜尋樹。

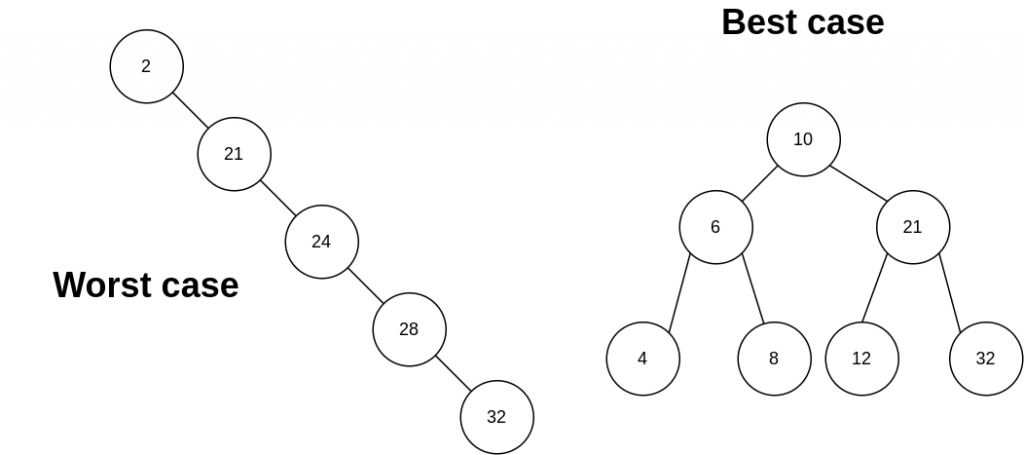
BST的特點是：對於每個節點，其左子樹中的所有值都小於該節點的值，而其右子樹中的所有值都大於該節點的值。

這個特性使得在BST中進行快速的查找、插入和刪除操作成為可能。

BST的應用十分廣泛，特別適合需要頻繁查找數據的情況，因為在平均情況下，查找操作的時間複雜度為，其中n是樹中節點的數量。然而，BST的性能取決於樹的平衡性。

如果樹的平衡性不好，可能會導致查找操作的時間複雜度變為，因此在實際應用中，需要注意保持樹的平衡，或者使用其他平衡二元搜尋樹結構，如紅黑樹，以確保性能。

// Binary Search Tree

class TreeNode(var key: Int) {
    var left: TreeNode? = null
    var right: TreeNode? = null
}

class BinarySearchTree {
    var root: TreeNode? = null

    fun insert(key: Int) {
        root = insertRec(root, key)
    }

    private fun insertRec(root: TreeNode?, key: Int): TreeNode {
        if (root == null) {
            return TreeNode(key)
        }

        if (key < root.key) {
            root.left = insertRec(root.left, key)
        } else if (key > root.key) {
            root.right = insertRec(root.right, key)
        }

        return root
    }

    fun search(key: Int): Boolean {
        return searchRec(root, key)
    }

    private fun searchRec(root: TreeNode?, key: Int): Boolean {
        if (root == null) {
            return false
        }

        if (key == root.key) {
            return true
        }

        return if (key < root.key) {
            searchRec(root.left, key)
        } else {
            searchRec(root.right, key)
        }
    }

    fun delete(key: Int) {
        root = deleteRec(root, key)
    }

    private fun deleteRec(root: TreeNode?, key: Int): TreeNode? {
        if (root == null) {
            return root
        }

        if (key < root.key) {
            root.left = deleteRec(root.left, key)
        } else if (key > root.key) {
            root.right = deleteRec(root.right, key)
        } else {
            if (root.left == null) {
                return root.right
            } else if (root.right == null) {
                return root.left
            }

            root.key = minValue(root.right!!)
            root.right = deleteRec(root.right, root.key)
        }

        return root
    }

    private fun minValue(node: TreeNode): Int {
        var current = node
        while (current.left != null) {
            current = current.left!!
        }
        return current.key
    }
}

fun main() {
    val tree = BinarySearchTree()

    // Insert some values into the BST
    tree.insert(50)
    tree.insert(30)
    tree.insert(20)
    tree.insert(40)
    tree.insert(70)
    tree.insert(60)
    tree.insert(80)

    // Search for values in the BST
    val keyToSearch = 40
    if (tree.search(keyToSearch)) {
        println("$keyToSearch found in the BST.")
    } else {
        println("$keyToSearch not found in the BST.")
    }

    // Delete a value from the BST
    val keyToDelete = 30
    tree.delete(keyToDelete)
    println("After deleting $keyToDelete:")
    if (tree.search(keyToDelete)) {
        println("$keyToDelete found in the BST.")
    } else {
        println("$keyToDelete not found in the BST.")
    }
}

AVL Tree

AVL tree 是一種自平衡的 Binary Search Tree，它的特點是在插入或刪除操作後會自動調整樹的結構，以保持樹的平衡性。

樹的平衡性是指樹中每個節點的左子樹和右子樹的高度差不超過1。

當向AVL樹中插入一個新節點或刪除一個節點時，系統會進行一系列的旋轉操作，以確保樹的平衡性不被破壞。

這些旋轉操作包括左旋、右旋、左右旋和右左旋等，它們的目標是讓樹的高度保持在合理的範圍內，從而確保查找、插入和刪除操作的時間複雜度都在的級別。

AVL樹的優點是能夠快速執行各種操作，但它需要在插入和刪除操作時進行平衡調整，這可能會導致額外的開銷。

class Node(var key: Int, var left: Node? = null, var right: Node? = null, var height: Int = 1)

class AVLTree {
    var root: Node? = null

    fun height(node: Node?): Int {
        return node?.height ?: 0
    }

    fun updateHeight(node: Node?) {
        node?.height = 1 + maxOf(height(node?.left), height(node?.right))
    }

    fun getBalance(node: Node?): Int {
        return if (node == null) 0 else height(node.left) - height(node.right)
    }

    fun rotateRight(y: Node?): Node? {
        val x = y?.left
        val T2 = x?.right

        x?.right = y
        y?.left = T2

        updateHeight(y)
        updateHeight(x)

        return x
    }

    fun rotateLeft(x: Node?): Node? {
        val y = x?.right
        val T2 = y?.left

        y?.left = x
        x?.right = T2

        updateHeight(x)
        updateHeight(y)

        return y
    }

    fun insert(node: Node?, key: Int): Node? {
        if (node == null)
            return Node(key)

        if (key < node.key)
            node.left = insert(node.left, key)
        else if (key > node.key)
            node.right = insert(node.right, key)
        else
            return node

        updateHeight(node)

        val balance = getBalance(node)

        // Left Heavy
        if (balance > 1) {
            if (key < node.left!!.key) {
                return rotateRight(node)
            } else {
                node.left = rotateLeft(node.left)
                return rotateRight(node)
            }
        }

        // Right Heavy
        if (balance < -1) {
            if (key > node.right!!.key) {
                return rotateLeft(node)
            } else {
                node.right = rotateRight(node.right)
                return rotateLeft(node)
            }
        }

        return node
    }

    fun insert(key: Int) {
        root = insert(root, key)
    }

    fun inorderTraversal(node: Node?) {
        if (node != null) {
            inorderTraversal(node.left)
            println(node.key)
            inorderTraversal(node.right)
        }
    }

    fun delete(key: Int) {
        root = delete(root, key)
    }

    fun minValueNode(node: Node?): Node? {
        var currentNode = node
        while (currentNode?.left != null)
            currentNode = currentNode.left
        return currentNode
    }

    fun delete(node: Node?, key: Int): Node? {
        if (node == null)
            return node

        if (key < node.key)
            node.left = delete(node.left, key)
        else if (key > node.key)
            node.right = delete(node.right, key)
        else {
            if (node.left == null || node.right == null) {
                val temp = if (node.left != null) node.left else node.right
                return if (temp == null) null else temp
            }

            val temp = minValueNode(node.right)
            node.key = temp!!.key
            node.right = delete(node.right, temp.key)
        }

        updateHeight(node)

        val balance = getBalance(node)

        // Left Heavy
        if (balance > 1) {
            if (getBalance(node.left) >= 0) {
                return rotateRight(node)
            } else {
                node.left = rotateLeft(node.left)
                return rotateRight(node)
            }
        }

        // Right Heavy
        if (balance < -1) {
            if (getBalance(node.right) <= 0) {
                return rotateLeft(node)
            } else {
                node.right = rotateRight(node.right)
                return rotateLeft(node)
            }
        }

        return node
    }

    fun search(node: Node?, key: Int): Node? {
        if (node == null || node.key == key)
            return node

        return if (key < node.key) search(node.left, key) else search(node.right, key)
    }
}

fun main() {
    val avlTree = AVLTree()

    // Insert some keys into the AVL tree
    avlTree.insert(10)
    avlTree.insert(20)
    avlTree.insert(30)
    avlTree.insert(40)
    avlTree.insert(50)
    avlTree.insert(25)

    println("Inorder traversal of AVL tree:")
    avlTree.inorderTraversal(avlTree.root)
    
    // Search for a key
    val keyToSearch = 30
    val foundNode = avlTree.search(avlTree.root, keyToSearch)
    if (foundNode != null) {
        println("Key $keyToSearch found in the AVL tree.")
    } else {
        println("Key $keyToSearch not found in the AVL tree.")
    }

    // Delete a key
    val keyToDelete = 40
    avlTree.delete(keyToDelete)
    println("Inorder traversal after deleting $keyToDelete:")
    avlTree.inorderTraversal(avlTree.root)
}

所有 Code 可以在 Github 找到 ～

感謝大家，明天見！！！