Algorithm

Hamiltonian Cycle 是圖論中的一個重要概念，它描述了在一個給定的圖中是否存在一條環路，該環路包含圖中的每個節點，並且只經過每個節點一次。

一個 Hamiltonian Cycle 是一條環路，它從一個節點開始，經過圖中的每個節點一次，然後回到起始節點，形成一個環路。這條環路中的節點不能重複，每個節點只能出現一次。

如果一個圖包含 Hamiltonian Cycle，則稱該圖是 Hamiltonian 圖，否則稱之為非 Hamiltonian 圖。

判定一個圖是否包含 Hamiltonian Cycle 是一個NP完全問題，這代表在一般情況下，找到 Hamiltonian Cycle 的問題是非常困難的，因為需要嘗試所有可能的環路組合。

Code

class HamiltonianCycle(private val graph: Array<IntArray>) {
    private val numVertices: Int = graph.size
    private val path: IntArray = IntArray(numVertices)

    private fun isSafe(v: Int, pos: Int, path: IntArray): Boolean {
        // Check if the vertex can be added to the path
        if (graph[path[pos - 1]][v] == 0) {
            return false
        }

        // Check if the vertex is not already in the path
        for (i in 0 until pos) {
            if (path[i] == v) {
                return false
            }
        }

        return true
    }

    private fun hamiltonianCycleUtil(pathPos: Int): Boolean {
        if (pathPos == numVertices) {
            // If all vertices are included in the path, check if it forms a cycle
            if (graph[path[pathPos - 1]][path[0]] == 1) {
                return true // Hamiltonian Cycle found
            }
            return false
        }

        for (v in 1 until numVertices) {
            if (isSafe(v, pathPos, path)) {
                path[pathPos] = v

                if (hamiltonianCycleUtil(pathPos + 1)) {
                    return true
                }

                path[pathPos] = -1 // Backtrack
            }
        }

        return false
    }

    fun findHamiltonianCycle(): Boolean {
        // Initialize the path array with -1
        for (i in 0 until numVertices) {
            path[i] = -1
        }

        // Start from the first vertex (0)
        path[0] = 0

        if (!hamiltonianCycleUtil(1)) {
            println("No Hamiltonian Cycle exists")
            return false
        }

        printHamiltonianCycle()
        return true
    }

    private fun printHamiltonianCycle() {
        println("Hamiltonian Cycle:")
        for (i in 0 until numVertices) {
            print("${path[i]} -> ")
        }
        println("${path[0]}") // Print the first vertex to complete the cycle
    }
}

// main function, entry point of the program
fun main() {
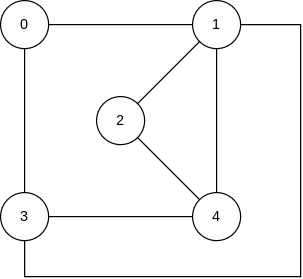
    val graph = arrayOf(
        intArrayOf(0, 1, 0, 1, 0),
        intArrayOf(1, 0, 1, 1, 1),
        intArrayOf(0, 1, 0, 0, 1),
        intArrayOf(1, 1, 0, 0, 1),
        intArrayOf(0, 1, 1, 1, 0)
    )

    val hamiltonianCycle = HamiltonianCycle(graph)
    hamiltonianCycle.findHamiltonianCycle()
}

class HamiltonianCycle(private val graph: Array<IntArray>)

包含了找尋 Hamiltonian Cycle 的主要方法。

• graph：儲存了圖的鄰接矩陣，它表示了圖的連接關係。
• numVertices：表示圖中節點的數量。
• path：用於儲存正在建立的 Hamiltonian Cycle。

private fun isSafe(v: Int, pos: Int, path: IntArray): Boolean

檢查是否可以將一個節點添加到目前的 Hamiltonian Cycle 中。

它檢查兩個條件：

• 這個節點是否與前一個節點有邊相連（根據鄰接矩陣）。
• 這個節點是否已經在目前的 Cycle 中出現過。

private fun hamiltonianCycleUtil(pathPos: Int): Boolean

使用回溯法來遞歸地尋找 Hamiltonian Cycle。

如果pathPos等於numVertices，則檢查最後一個節點是否與起始節點相連，如果是則找到 Hamiltonian Cycle。

否則，遍歷所有節點，如果可以安全地將節點添加到 Cycle 中，則進行遞歸呼叫，並在遞歸返回後進行回溯。

fun findHamiltonianCycle(): Boolean

初始化路徑數組並啟動查找 Hamiltonian Cycle 的過程。

• 從第一個節點開始（通常是0號節點）。
• 如果找不到 Hamiltonian Cycle，則輸出 "No Hamiltonian Cycle exists"。
• 如果找到 Hamiltonian Cycle，則輸出該 Cycle。

private fun printHamiltonianCycle()

用於輸出找到的 Hamiltonian Cycle。

Terminal 輸出

0 -> 1 -> 2 -> 4 -> 3 -> 0

所有 Code 可以在 Github 找到 ～

感謝各位讀者，我們明天見！