昨天用快速傅立葉轉換做一維的單狹縫，
助教表示：有一維就有二維

抓緊了各位：

import numpy as np
import matplotlib.pyplot as plt

#定義計算二進制的位元反轉函數
def bit_reversal(number, bitsize):
    binary = bin(number) #將整數轉換為二進制表示
    reverse = binary[-1:1:-1] #反轉二進位字符串
    reverse = str(reverse) + "0" * (bitsize - len(reverse)) #根據位元大小 (bitsize)，對反轉後的二進位字符串補0
    return int(reverse, 2) #將反轉後的二進制數轉為整數

#定義根據蝴蝶圖進行數據合併的FFT_unit函數   
def FFT_unit(array_e, array_o): #array_e和array_o 分別是原始數據中所有偶數和奇數索引的位置
    N = len(array_e) * 2  #將一個長度為 N 的陣列拆分成兩個長度為 N/2 的陣列進行處理
    W_array = np.array([np.exp(complex(0, -2 * np.pi * a / N)) for a in range(int(N / 2))]) #製作傅立葉變換中的旋轉因子
    output1 = array_e + W_array * array_o #將兩組數據合併
    output2 = array_e - W_array * array_o #將兩組數據合併
    return np.hstack((output1, output2))

# 一維的快速傅立葉轉換
def FFT_1D(array_i): #array_i為狹縫空間域數據
    length = len(array_i) #取 array_i 的長度，得輸入數據的總數量
    bit_size = int(np.log2(length)) #計算輸入數據長度的對數（以 2 為底），即 log2(length)，用來確定位反轉(bit reversal)所需的位數。
    rearrange = [] #初始化一個空列表，稍後將用來存放經過位反轉後重新排列的數據
    for i in range(length): 
        bit_reverse = bit_reversal(i, bit_size) #計算i 的位反轉結果。例: i 是二進位的 001（十進位為 1），在三位的情況下，它的位反轉結果是 100（十進位為 4）
        tmp_array = np.array([array_i[bit_reverse]]) #根據位反轉後的I，從 array_i 中取出對應的元素，並將其轉換為一個array
        rearrange.append(tmp_array) #將重新排列的array加入到 rearrange 列表
    output = rearrange
    for s in range(bit_size): #以外部迴圈控制 FFT 的計算層數（每一層的計算都相當於蝴蝶圖中的一層操作)
        tmp_list = [] #初始化一個空列表
        for j in range(int(len(output) / 2)): #遍歷目前數據的1/2
            tmp_array = FFT_unit(output[2 * j], output[2 * j + 1]) #帶入FFT_unit對數據執行蝴蝶操作，產生新的頻域數據
            tmp_list.append(tmp_array) #將數據的運算結果加入到 tmp_list 中
        output = tmp_list
    return output[0] #得最終的計算結果

# 定義二維快速傅立葉轉換函數
def FFT_2D(array_i):  #array_i為狹縫空間域數據
    len_x, len_y = array_i.shape #取出行數 len_x 和列數 len_y
    output_array = np.zeros((len_x, len_y), dtype=complex) #定義行列為複數array 
    for i in range(len_x):
        output_array[i, :] = FFT_1D(array_i[i, :]) #對每一行進行一維 FFT 計算
    tmp_array = output_array #將 output_array 的內容複製到 tmp_array
    for j in range(len_y):
        output_array[:, j] = FFT_1D(tmp_array[:, j]) #對每一列進行一維 FFT 計算
    return output_array      

# 平移，快速傅立葉轉換計算結果的中心點在K/2，將其平移回0
def FT_shift_2D(array_i):
    len_x, len_y = array_i.shape #取出行數 len_x 和列數 len_y
    shift_x = int(len_x / 2) #x平移長度為len_x一半的整數
    shift_y = int(len_y / 2) #y平移長度為len_y一半的整數
    return np.roll(array_i, (shift_x, shift_y), (0, 1)) #使用 np.roll 函數對 array_i 進行平移操作，shift_x shift_y表示偏移量，(0, 1)表示偏移操作的軸，0 代表行軸，1 代表列軸



# 定義單狹縫函數
def single_slit(x, d):
    if -d / 2 < x < d / 2:
        return 1 / d
    else:
        return 0

# 畫圖範圍
D = 20
# 解析度
N = 256
# 狹縫寬度
d = 1

# 定義空間的list
x_list = [-D / 2 + D * i / N for i in range(N)]
y_list = [-D / 2 + D * j / N for j in range(N)]
x_array, y_array = np.meshgrid(x_list, y_list)

# 定義起始光場的list
# 定義方孔
source_list = [[
    single_slit(x_list[i], d) * single_slit(y_list[j], d)
    for i in range(N)]
    for j in range(N)]

# 轉成陣列並做快速傅立葉轉換
source_array = np.array(source_list) #將 source_list 轉換為 NumPy 陣列
FFT_array = FFT_2D(source_array) #將source_array帶入FFT_2D函數
FFT_array = FT_shift_2D(FFT_array) #將上面結果進行FT_shift_2D中心化
intensity = [[abs(FFT_array[i, j]) for i in range(N)] for j in range(N)] #帶入上述結果取絕對值得光強

# 畫圖
plt.subplot(2, 1, 1)
plt.contourf(source_array, levels=90, cmap="grey")
plt.title("Source Field - Square Aperture")
plt.subplot(2, 1, 2)
plt.contourf(intensity, levels=90, cmap="grey")
plt.title("Intensity after 2DFFT")
plt.subplots_adjust(hspace=0.4)
plt.show()

得出圖如下：

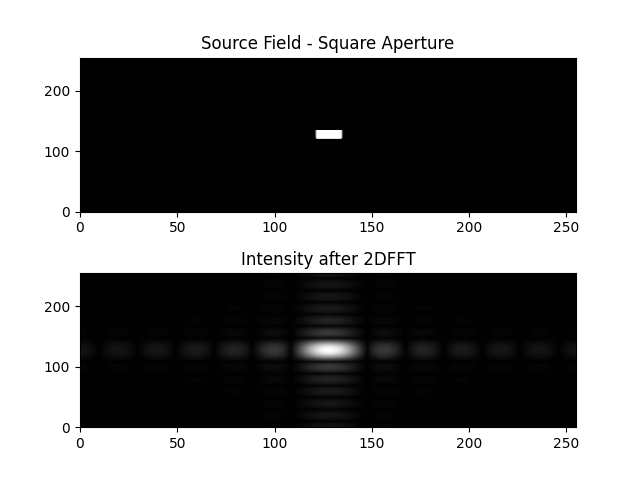
今天的內容主要以昨天的一維傅立葉轉換作為基礎，再加上二維轉換和置中函數，最後以contourF函數畫出二維圖面。

是不是很神奇呢？讓我們再度讚頌助教與AI！大家還活著的話明天繼續唷。