53.MAXIMUM SUBARRAY
1.題目理解:給定一個整數陣列 NUMS，找出一個「連續子陣列（SUBARRAY）」（包含至少一個元素），其總和最大，並回傳其總和。
2.解題觀念:

• 使用變數current_sum 來記錄目前為止的最大子陣列和。
• 如果 current_sum< 0，就丟棄前面的累積，重新從當前數字開始。
• 同時更新 max_sum來記錄目前為止的最大總和。
  3.程式碼說明:
  INT MAXSUM = NUMS[0];
• 一開始把「最大總和」設為陣列的第一個元素，因為至少會有一個元素存在。
• 它會隨著程式執行不斷更新，直到找到最大那段的總和。
  INT CURRENTSUM = NUMS[0];
• 這個變數用來記錄目前這段正在累積的子陣列總和。
• 如果發現這段總和變負的，之後我們會直接重新開始一段新的計算（代表負值會讓整體結果更
  差）。
  FOR (INT I = 1; I < NUMS.LENGTH; I++)
• 從第 2 個數字開始走訪陣列，因為第 1 個已經用在初始化。
• CURRENTSUM = MATH.MAX(NUMS[I], CURRENTSUM + NUMS[I]);
  這行是關鍵邏輯（KADANE'S ALGORITHM）：
  比較兩種可能：
  1.只取目前這個數字（NUMS[I]）
  2.把這個數字加進目前累積的總和（CURRENTSUM + NUMS[I]）
  3.為什麼？
• 如果前面累加的 CURRENTSUM 是負數，加上後面數字反而變更小，那就不如捨棄，重新開始。
• 所以取兩者的最大值。
  MAXSUM = MATH.MAX(MAXSUM, CURRENTSUM);
• 每次都比較看看：目前這段的總和（CURRENTSUM）有沒有比目前已知的最大總和（MAXSUM）還要大，有的話就新。
  RETURN MAXSUM;
• 走完整個陣列後，回傳累積到的最大總和。
  假設 NUMS = [-2,1,-3,4,-1,2,1,-5,4]→ 最終回傳結果為 6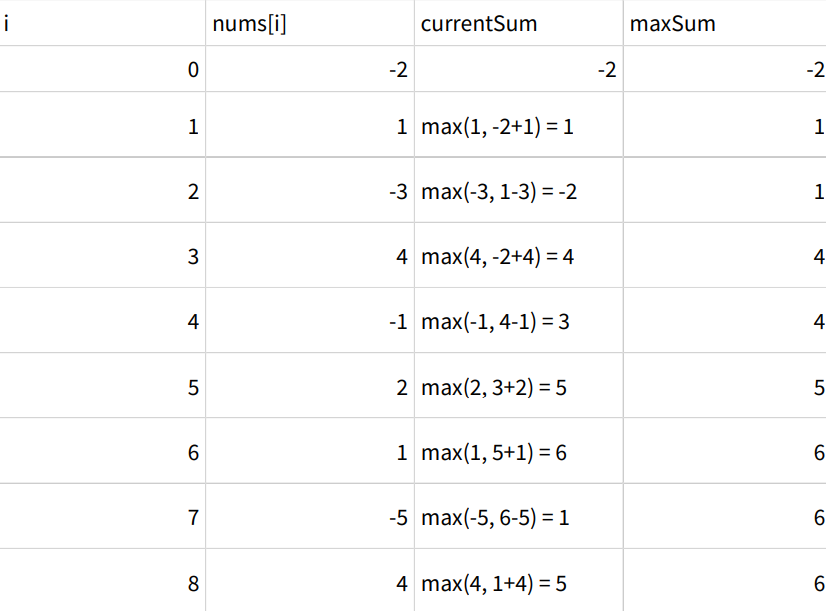
  4.程式碼截圖:
  
  5.學習心得:這次選擇的題目是之前老師學期結束後有放一些可以自己挑戰的題目，此題就是其中的一題。透過這次的練習不僅讓我可以自己學習解Leetcode也了解到原來這些演算法都可以應用在生活上，像我這次所運用到的
  Maximum Subarray 演算法雖然看似簡單，但應用範圍極廣。只要有「連續資料 + 要找最大增幅/最大總和」的情況，都可以使用這個演算法，例如金融、氣象、財務、健康監測等領域，皆有實際應用價值。雖然我還是不能獨自完成一個Leetcode題目，但是我還是從ChatGPT的回答中學習到很多，也越來越看得懂程式碼的應用，這是我這次練習中收穫最大的地方。