今天是紀錄LeetCode解題的第五十一天
是一題困難題

第五十一題題目：The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

n皇后問題是指在n * n的棋盤上放置n個皇后，使得任兩個皇后不會互相攻擊的問題
給定一個整數n，傳回n皇后問題的所有不同解，可以按任意順序傳回答案
每個解決方案都包含n個皇后放置的不同棋盤配置，其中'Q'和' . '分別表示皇后和空格

解題思路

這題的皇后可以在上下左右以及斜對角線無限距離攻擊，
因此我們放置的位置要符合

1. 同一列只能有一個皇后
2. 同一行只能有一個皇后
3. 同一條對角線（含左上到右下、右上到左下）只能有一個皇后

我們可以簡化放置時檢查的過程，以一列一列來進行放置，每次放置皇后時，檢查它的同一行、左上對角線和右上對角線是否有其他皇后存在，如果沒有則放置，有的話則往下一行檢查是否可以放置，那如果發現這一列每一個位置都不能放置，就代表上一列所放的位置是不正確的，就回溯到上一列找其他位置放置

程式碼

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        board = [["."] * n for _ in range(n)]
        res = []
        backtracking(0,n,board,res)
        return res

def backtracking(row,n,board,res):
    if row == n:
        res.append(["".join(r) for r in board])
        return
    for col in range(n):
        if check(row,col,n,board):
            board[row][col] = "Q"
            backtracking(row + 1,n,board,res)
            board[row][col] = "."

def check(row,col,n,board):
    for i in range(n):
        if board[i][col] == "Q":
            return False
    #左上
    i , j = row - 1, col - 1
    while i >= 0 and j >= 0:
        if board[i][j] == "Q":
            return False
        i -= 1
        j -= 1
    #右上
    i , j = row - 1, col + 1
    while i >= 0 and j < n:
        if board[i][j] == "Q":
            return False
        i -= 1
        j += 1
    return True

執行過程

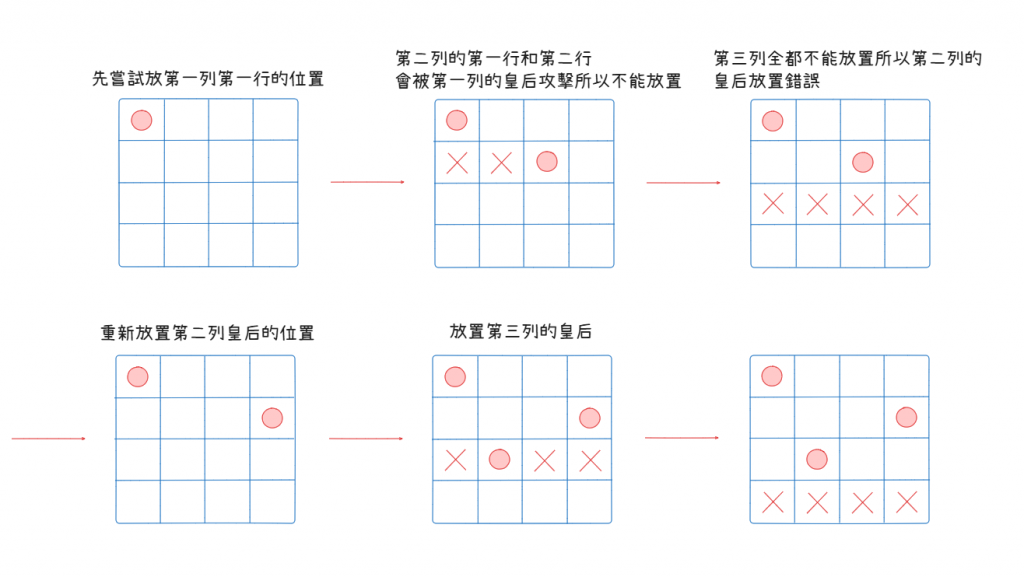
最後發現第四列全都不能放置，返回第三列，但發現第三列也沒有其他行可以放置，再回到第二列，發現第二列可以放置的位置也都嘗試過了，所以代表皇后不能放置在第一列第一行，我們改放在第一列第二行

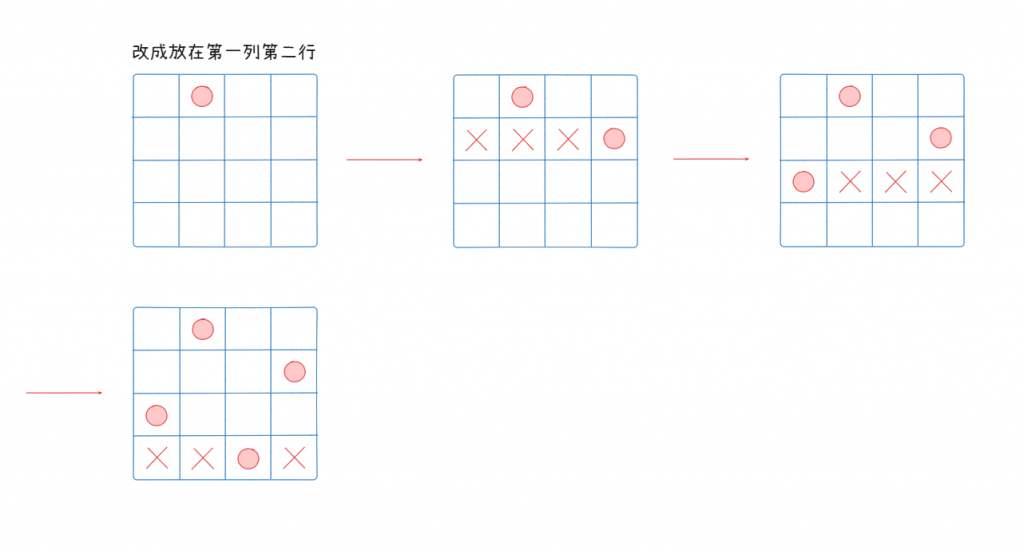
執行過程如上，以每一列為基準去放置皇后，這樣我們就只需要檢查同一行、左上對角線和右上對角線即可