

公式部分偏微分上面計算出來有錯,於下面留言中有更正
之後選一組(a,b)作為起點,再配合 梯度下降 選合適的步長逼近最小值
我的想法和你一樣 概念是這樣不過code部分我很有障礙..
這部分可以和你討論嗎QQ
我早上稍微寫了一下,覺得這個函式有可能不適合用梯度下降去做
殘餘的程式碼(暫時沒空閒繼續玩,就先放著)
# 更正於後面留言
我想請問 假如將這組數據轉為線性 就是ln(y/x) = ln(a) + bx
這樣的做法呢 是否就可以梯度下降 轉換後做出來是參數是2.268178503和-2.473308766 這樣表示以後收集到數據都要先做轉換再帶到這組ln(y/x) = ln(a) + bx 來去做預測呢?
因為非線性的關西所以這組函數的確可能會卡住不是合去做

EXCEL算出來的最佳值是這樣
想知道他們都怎麼fit出來的
謝謝您的回答 萬分感激!
線性的話不用梯度下降,直接偏微分後=0 解聯立就可
轉換後的 2.268178503 跟 -2.473308766 的確算得出來
只是目前我還不知道怎麼找 9.897362 跟 -2.5318...
import math
# 讀取資料點的檔案,該檔案每行為一組 x,y ,以空白分隔
def readFile(fName):
datas=[]
with open(fName, 'r', encoding='utf-8') as f:
for line in f:
arr=line.strip().split()
x=float(arr[0])
y=float(arr[1])
z=math.log(y/x)
datas.append((x,y,z))
return datas
return None
#求解,利用偏微分=0去解聯立
def getSolution(dataPoints):
sumX=0
sumX2=0
sumXY=0
sumY=0
sum1=len(dataPoints)
for p in dataPoints:
x=p[0]
y=p[2]
sumX+=x
sumX2+=x*x
sumXY+=x*y
sumY+=y
d= sumX2*sum1-sumX*sumX
dx=sumXY*sum1-sumY*sumX
dy=sumX2*sumY-sumX*sumXY
return (dx/d, dy/d)
dataPoints=readFile('aaa.txt')
sol=getSolution(dataPoints)
print(sol)
print('a=%f, b=%f' % (math.exp(sol[1]), sol[0]))
對了 excel 那個 9.897362 跟 -2.5318 是怎麼求出來的可以教一下嗎?函式名稱是?
用excel裡面的規劃求解他會幫你算出來
所以才有這個最佳解
希望還是可以用梯度下降來解這一題QQ
對了我發現9.897362是 2.268178503自然對數 也就是推回去而已
2.268178503 的自然對數是 9.661786 應該還差一些
轉換後算出來的很接近正確答案是很合理的
只是還差一些
我有做出來了,上面的公式對 b 的偏微分有計算錯
重新算偏微分的部分應該是: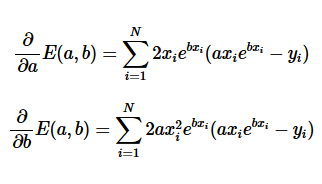
程式碼部分,你再看自己需求調整一下。
import math
# 讀取資料點的檔案,該檔案每行為一組 x,y ,以空白分隔
def readFile(fName):
datas=[]
with open(fName, 'r', encoding='utf-8') as f:
for line in f:
arr=line.strip().split()
datas.append((float(arr[0]), float(arr[1])))
return datas
return None
#計算在(a,b)的誤差
def Err(a, b, dataPoints):
sum=0
for p in dataPoints:
x=p[0]
y=p[1]
sum+=math.pow(y-a*x*math.exp(b*x), 2)
return sum
#計算在(a,b)的梯度,回傳 (da, db, len) 其中 len 為 (da,db)向量的長度
def Grad(a, b, dataPoints):
sumA=0
sumB=0
for p in dataPoints:
x=p[0]
y=p[1]
t=x*math.exp(b*x)
t=2*t*(a*t-y)
sumA+=t
sumB+=a*x*t
return (sumA, sumB, math.sqrt(sumA*sumA+sumB*sumB))
# 利用轉換後的線性方法求近似解作為起始值
def getInitialVal(dataPoints):
sumX=0
sumX2=0
sumXY=0
sumY=0
sum1=len(dataPoints)
for p in dataPoints:
x=p[0]
y=math.log(p[1]/p[0])
sumX+=x
sumX2+=x*x
sumXY+=x*y
sumY+=y
d= sumX2*sum1-sumX*sumX
dx=sumXY*sum1-sumY*sumX
dy=sumX2*sumY-sumX*sumXY
return (math.exp(dy/d), dx/d)
#求解
def getSolution(a, b, r, dataPoints):
err=Err(a, b, dataPoints)
count=0
while(count<2000 and (count==0 or (grad[2]>1e-30 and d>=1e-10))):
count=count+1
print('(a, b, err)=(%f, %f, %f)' % (a , b , err))
grad=Grad(a, b, dataPoints)
print('(da, db, len)=(%f, %f, %e)' % grad)
print(count)
if(grad[2]>1e-10):
d=r
while(d>=1e-10):
newA=a-d*grad[0]/grad[2]
newB=b-d*grad[1]/grad[2]
newErr=Err(newA, newB, dataPoints)
if(newErr <= err):
err=newErr
a=newA
b=newB
break
else:
d=d/2
else:
break
return (a,b,err)
dataPoints=readFile('aaa.txt')
initVal=getInitialVal(dataPoints)
sol=getSolution(initVal[0], initVal[1], 1, dataPoints)
print(sol)
大大 你太神了
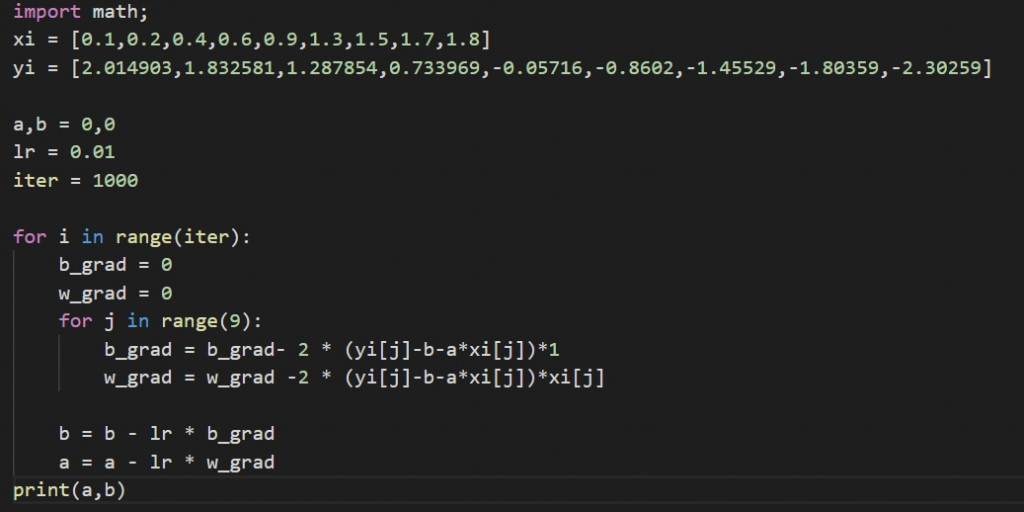
想請問這個也是梯度下降對吧
如果是的話這些方法差別在哪邊呢
真的非常感謝大大
他那個不是擬合線性函數 ax+b 嗎?
刪除 (手機發文連按到)
需要解聯立方程式,看起來會用到ln...然後我log/ln忘得差不多了@@
跑去複習指數律、對數律 ...
您說現在有資料點,我就當作您有多組正確的 x,y
也不用真的算出值,交給計算機XD