大家好,最近拿到一筆有50個維度的資料,所以研究了PCA的使用,但不太懂,遇到了幾個問題想請教,這邊先以iris做例子:
data("iris")
pca <- prcomp(formula = ~ Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,data = iris)
summary(pca)
top2.pca.eigenvector <- pca$rotation[, 1:2]
top2.pca.eigenvector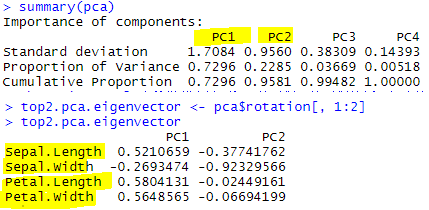
問題1: PCA是用來刪除解釋能力差的變數嗎?
問題2: 假設我只選擇第二個主成分PC2,Petal.Length線性組合數最小,代表可刪除?

我碩士論文剛好跟 PCA有一點關係,依照模糊的印象 (畢業10幾年了)
你的第一主成分 可以解釋 72.96 % 的原來資料
第二主成分 可以解釋 22.85 % 的原來資料
第一主成分 + 第二主成分 共可以解釋 95.81% 的原來資料
一般來講 可以解釋 95.81% 以已經很高了 , 所以第三主成分,第四主成分可以忽略不管
PCA1 + PCA2 = 95.81% 原資料代表性
我這裡不知道你所謂的50個維度是指50個變數量,還是指有50筆資料
我把他先當作50筆資料
PCA1= 0.5210659 Sepal. Length -0.2693474 Sepal. width +0.5804131 Petal.
Length +0.5648565 Petal. width
PCA2=-0.37741765 Sepal. Length -0.92329566 Sepal. width -0.02449161 Petal.
Length - 0.06694199 Petal. width
PCA= 常數 PCA1 + 常數 PCA2 = 0.7296 PC1 + 0.2285 PC2
問題1: PCA是用來刪除解釋能力差的變數嗎?
不完全對,事實上他無法刪除解釋能力差的變數,他是利用幾個主成分來代表原來資料的解適能力百分比
這不像類神經網路,類神經網路可以得到解釋能力差的變數,然後把這個變數剃除
問題2: 假設我只選擇第二個主成分PC2,Petal.Length線性組合數最小,代表可刪除?
錯
PCA2的解釋能力只有 22.85%
一般解釋能力至少要80%
因此最少要用 PCA1+PCA2 =95.81%
這只代表說 Petal.Length 在PCA2 中,解釋能力最低
但別忘了 整個 PCA2只有 22.85%的解釋能力
這其實意味著,每一個 PCA1~PCAn 都有一個特定的特徵方向
在 PCA2這個特徵方向中,Petal.Length 相關性,或解釋能力最低
但不代表可以把它刪除
因為他只在 PCA2最低, 但在 PCA1中,他不是最低,別忘了 PCA1有 72.96%的解釋能力
而且他在 PCA1中係數最大,你怎能把他刪除,絕對不能
至於該怎麼解釋,依我模糊的印象
依據上面的資料
解釋如下
2.第二主成分,解釋變異 22.85 %
Sepal. width 萼片寬度 ,這個係數值 -0.92329566 是 PCA2最低的
一句話解釋
PCA2有22.85%解釋能力,其中又以 萼片寬度 這個變數,解釋能力最強(或最弱)
參考,這篇看看 https://tinyurl.com/two57cy
你可以看他寫的摘要 :
查的葉部型態特徵包括葉片長度、葉片寬度、葉柄長度、葉尖角度、葉基角度及葉片長寬比。經主成份分析,前三主成份軸共可解釋80.83%的變異量。透過主成份分析結果可得知,葉尖角度與葉基角度為主要代表性狀。調查的花器型態特徵包括花朵直徑、主瓣長度、主瓣寬度、雌蕊長度、雄蕊長度、雄蕊數目以及花朵顏色。經主成份分析,前四主成份軸共可解釋86.26%的變異量。透過主成份分析結果可得知,雄蕊數目、雄蕊長度與花朵直徑為主要代表性狀。
這一段說明 PCA不是在刪減變數,是要找解釋變異量
或者 Google 安德森鳶尾花卉 的一些多變量分析 研究