題目如下: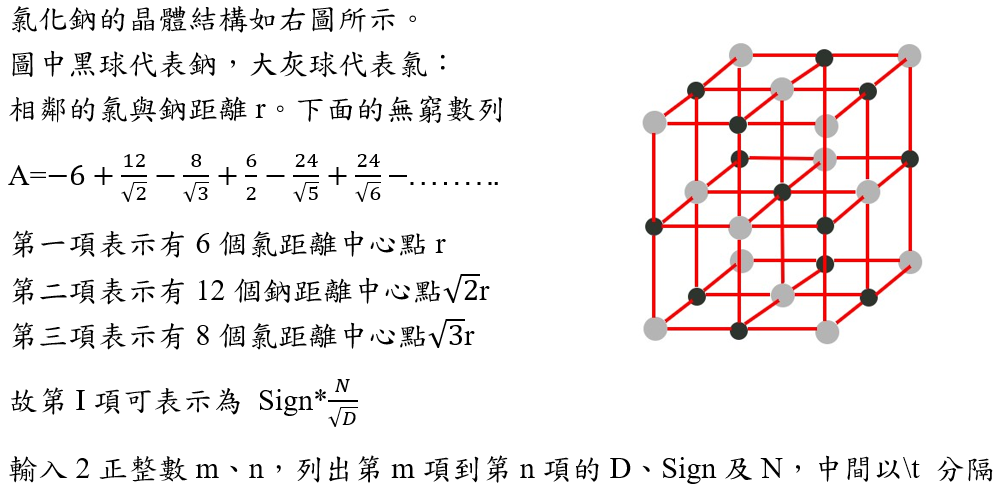
昨天詢問老師,老師有給提示,是要用x^2+y^2+z^2==h^2的概念作題。我打到最後卡在這:
#include <iostream>
#include <cmath>
using namespace std;
int main(void){
int a,b,h,i,j,k,N=0;
char sign;
cin >> a >> b;
for(h=a;h<=b;h++){
if(h%2==1){
sign='-';
}
else{
sign='+';
}
for(i=0;i<h+1;i++){
for(j=0;j<h+1;j++){
for(k=0;k<h+1;k++){
if(((i^2)+(j^2)+(k^2))==(h^2)){
N=N+2;}}}}
cout << h << "\t" << sign << "\t" << N << "\n";
N=0;
}
return 0;
}
我是把X,Y,Z軸值用i,j,k的for迴圈呈現,但好像有問題。請問有大大能幫我看看是哪裡邏輯錯誤嗎?
---更---
感謝大大解惑,平方那邊的問題解決了。我現在把ijk那邊迴圈的初始值改成-h,最裡面if迴圈的N+2改成N+1,如下:
#include <iostream>
#include <cmath>
using namespace std;
int main(void){
int a,b,h,i,j,k,N=0;
char sign;
cin >> a >> b;
for(h=a;h<=b;h++){
if(h%2==1){
sign='-';
}
else{
sign='+';
}
for(i=0-h;i<h+1;i++){
for(j=0-h;j<h+1;j++){
for(k=0-h;k<h+1;k++){
if(((i*i)+(j*j)+(k*k))==(h*h)){
N=N+1;
}
}
}
}
cout << h << "\t" << sign << "\t" << N << "\n";
N=0;
}
return 0;
}
但還是有bug,請問還有哪裡有問題?

提供參考
我的作法是慢慢加大盒子大小
每次增加盒子大小就把「座標點」寫到陣列(可排序後輸出)
座標點的表達我是規定從大排到小
例如:(5,5,2) 這組數字,代表了 個座標點
#include <iostream>
#include <vector>
#include <algorithm>
class Point
{
private:
unsigned x, y, z; //座標(限定 x >= y >= z >= 0)
unsigned step; //步長(奇偶數決定正負號)
unsigned r2; //半徑平方
unsigned n; //對稱點數目
bool xAxis; //是否在 x 軸上
public:
Point(unsigned, unsigned, unsigned); //建構,參數請從大排到小
bool isXAxis(); //這個點是否在 x 軸上
unsigned _getNum(); //取得對稱點數目
bool operator<(const Point &); //用於 std::sort
friend std::ostream &operator<<(std::ostream &, const Point &); //輸出
};
class BoxPoints
{
private:
unsigned r; //盒子中心到表面的最短距離
unsigned idx; //讀取到的位置
std::vector<Point> points; //收集到的點
void _extendRadius(); //加大盒子大小,更新 r、points、idx
public:
BoxPoints();
Point getNext(); //取得下一個點
};
int main()
{
BoxPoints box;
for (int i = 0; i < 20; ++i)
{
std::cout << box.getNext();
}
return 0;
}
Point::Point(unsigned px, unsigned py, unsigned pz)
{
x = px;
y = py;
z = pz;
step = px + py + pz;
r2 = px * px + py * py + pz * pz;
n = _getNum();
xAxis = (y == 0 && z == 0);
}
bool Point::isXAxis()
{
return xAxis;
}
unsigned Point::_getNum()
{
unsigned t = 1;
if (x > 0)
{
t <<= 1;
}
if (y > 0)
{
t <<= 1;
}
if (z > 0)
{
t <<= 1;
}
if (x == y)
{
if (y == z)
{
return t;
}
else
{
return t * 3;
}
}
else
{
if (y == z)
{
return t * 3;
}
else
{
return t * 6;
}
}
}
bool Point::operator<(const Point &p)
{
return r2 != p.r2 ? (r2 < p.r2) : (step < p.step);
}
std::ostream &operator<<(std::ostream &os, const Point &p)
{
os << "(" << p.x << "," << p.y << "," << p.z << ") => "
<< (p.step % 2 ? "-" : "+") << p.n << "/" << p.r2 << " (" << p.step << ")\n";
return os;
}
BoxPoints::BoxPoints()
{
r = 0;
idx = 0; //讀取的索引
_extendRadius();
}
Point BoxPoints::getNext()
{
Point p = points[idx++];
if (p.isXAxis())
{
points.erase(points.begin(), points.begin() + idx);
idx = 0;
_extendRadius();
}
return p;
}
void BoxPoints::_extendRadius()
{
unsigned x = ++r;
for (int y = x; y >= 0; --y)
{
for (int z = y; z >= 0; --z)
{
points.push_back(Point(x, y, z));
}
}
std::sort(points.begin(), points.end());
}
/*
輸出結果
(1,0,0) => -6/1 (1)
(1,1,0) => +12/2 (2)
(1,1,1) => -8/3 (3)
(2,0,0) => +6/4 (2)
(2,1,0) => -24/5 (3)
(2,1,1) => +24/6 (4)
(2,2,0) => +12/8 (4)
(3,0,0) => -6/9 (3)
(2,2,1) => -24/9 (5)
(3,1,0) => +24/10 (4)
(3,1,1) => -24/11 (5)
(2,2,2) => +8/12 (6)
(3,2,0) => -24/13 (5)
(3,2,1) => +48/14 (6)
(4,0,0) => +6/16 (4)
(4,1,0) => -24/17 (5)
(3,2,2) => -24/17 (7)
(3,3,0) => +12/18 (6)
(4,1,1) => +24/18 (6)
(3,3,1) => -24/19 (7)
*/
感謝大大回應!我已經用我上面的程式結構寫完了,但有runtime error的問題(輸入的數太大,導致運算時間太久)。請問有簡化我的三層巢氏的方法嗎?
要加快速度,比較簡單的方式是:直接跑最大的區域,記錄下「半徑平方」與「個數」之間的關係。之後輸出時查詢紀錄就可。這樣可以避免內部方塊重複計算的時間。
#include <iostream>
#include <map>
int main(void)
{
int a, b, h, i, j, k, r, N;
char sign;
std::map<int, int> record;
//輸入範圍
std::cin >> a >> b;
//直接跑最大的區域 (-b~b, -b~b, -b~b),並記錄個數
for (i = -b; i <= b; i++) {
for (j = -b; j <= b; j++) {
for (k = -b; k <= b; k++) {
r = i * i + j * j + k * k;
if (record.find(r) == record.end()) {
record[r] = 1; //如果紀錄中沒有 r 設為 1
} else {
record[r] += 1; //若已有紀錄,增加 1
}
}
}
}
//輸出時直接從記錄中去找
for (h = a; h <= b; ++h) {
if (record.find(h) != record.end()) {
N = record[h];
sign = h % 2 ? '-' : '+';
std::cout << h << "\t" << sign << "\t" << N << "\n";
}
}
return 0;
}
接續上面,進一步利用對稱關係,可以再加快速度
(迴圈數大概是原本的 1/32 左右)
#include <iostream>
#include <map>
int getNum(int x, int y, int z)
{
int t = 1;
if (x > 0) {
t <<= 1;
}
if (y > 0) {
t <<= 1;
}
if (z > 0) {
t <<= 1;
}
if (x == y) {
if (y == z) {
return t;
} else {
return t * 3;
}
} else {
if (y == z) {
return t * 3;
} else {
return t * 6;
}
}
}
int main(void)
{
int a, b, h, i, j, k, r, N;
char sign;
std::map<int, int> record;
//輸入範圍
std::cin >> a >> b;
//直接跑最大的區域,並記錄個數
for (i = 1; i <= b; i++) {
for (j = 0; j <= i; j++) {
for (k = 0; k <= j; k++) {
//注意這邊 i >= j >= k,用 getNum 算對稱點個數
r = i * i + j * j + k * k;
if (record.find(r) == record.end()) {
record[r] = getNum(i, j, k); //如果紀錄中沒有 r 設為個數
} else {
record[r] += getNum(i, j, k); //若已有紀錄,增加個數
}
}
}
}
//輸出時直接從記錄中去找
for (h = a; h <= b; ++h) {
if (record.find(h) != record.end()) {
N = record[h];
sign = h % 2 ? '-' : '+';
std::cout << h << "\t" << sign << "\t" << N << "\n";
}
}
return 0;
}
sorry大大,我還看不太懂你打的,但能請你幫我從我修改好的來優化嗎?
#include <iostream>
#include <cmath>
using namespace std;
int main(void){
int a,b,h,i,j,k,N=0;
char sign;
cin >> a >> b;
for(h=a;h<=b;h++){
if(h%2==1){
sign='-';
}
else{
sign='+';
}
for(i=0-h;i<h+1;i++){
for(j=0-h;j<h+1;j++){
for(k=0-h;k<h+1;k++){
if(((i*i)+(j*j)+(k*k))==h){
N=N+1;
}
}
}
}
cout << h << "\t" << sign << "\t" << N << "\n";
N=0;
}
return 0;
}
先前我提到
要加快速度,比較簡單的方式是:直接跑最大的區域,記錄下「半徑平方」與「個數」之間的關係。之後輸出時查詢紀錄就可。這樣可以避免內部方塊重複計算的時間。
就是從你寫的東西改的,已經盡量不改太多了
你看不懂可能是沒學過內建的容器(例如 Map)
下面先把 Map 改成一般陣列,先看懂我先前表達的意思
之後還是建議學一下 Map 的用法
#include <iostream>
int main(void)
{
int a, b, h, i, j, k, r, N;
char sign;
int* record;
//輸入範圍
std::cin >> a >> b;
//改用陣列紀錄,缺點是比起 Map 很浪費空間
//b 的 3 次方很浪費記憶體,測試時不要輸入太大
record = new int[b * b * b]();
//直接跑最大的區域 (-b~b, -b~b, -b~b),並記錄個數
for (i = -b; i <= b; i++) {
for (j = -b; j <= b; j++) {
for (k = -b; k <= b; k++) {
r = i * i + j * j + k * k;
record[r] += 1;
}
}
}
//輸出時直接從記錄中去找
for (h = a; h <= b; ++h) {
if (record[h] > 0) {
N = record[h];
sign = h % 2 ? '-' : '+';
std::cout << h << "\t" << sign << "\t" << N << "\n";
}
}
delete[] record;
return 0;
}
感謝!但後來老師有給提示是說不用掃整個立方體,所以三層巢氏應該是沒錯的,只是迴圈的範圍問題而已。
ps. 老師有故意input 9000 9010,所以全部掃完應該是沒辦法qwq。
修改後
#include <iostream>
#include <cmath>
using namespace std;
int main(void){
int a,b,h,i,j,k,N=0;
char sign;
cin >> a >> b;
for(h=a;h<=b;h++){
if(h%2==1){
sign='-';
}
else{
sign='+';
}
for(i=-h;i<=h;i++){
for(j=-h;j<=h;j++){
for(k=-h;k<=h;k++){
if(((i*i)+(j*j)+(k*k))==(h*h)){
N=N+1;
}
}
}
}
cout << h << "\t" << sign << "\t" << N << "\n";
N=0;
}
return 0;
}