我用C語言寫一個關於Dijkstra演算法的練習，請問有哪些地方可以優化？

shazbot001 2023-10-23 17:11:04 ‧ 1462 瀏覽

分享至

大家好，我第一次發文，有甚麼違反規定的地方麻煩告知。
我在練習C語言，用C寫一個關於Dijkstra演算法的練習，結果是寫出來了，但感覺寫得不好，想請問有哪些地方可以優化的？不知道這問題合不合適？
先感謝各位回答了。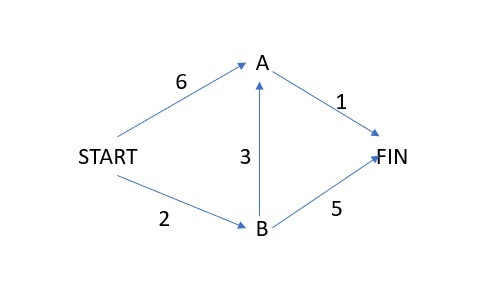

從START點走道FIN點，箭頭是單行道。START->A為6，START->B為2，B->A為3，B->FIN為5，A->FIN為1，找出最短路徑。

#include <stdio.h>
#include <string.h>
#define MAX_INT 2147483647
#define MAX_NODE_LENGTH 10
typedef struct path {
  char *node;
  int distance;
}PATH;
typedef struct graph{
  char *node;
  PATH *graph_path;            //一開始設成這樣PATH graph_path[MAX_PATH];，結果無法一起賦值，只好將PATH拉出去單獨宣告，然後忘了改成ptr，就讀不到資料
  int member;
}GRAPH;
typedef struct mileage{
  char *node;
  int total;
}MILEAGE;
typedef struct parent{
  char *node;
  char father[MAX_NODE_LENGTH];
}PARENT;
void findShortestPath(GRAPH *start_to_fin, MILEAGE *shortest_mileage, PARENT *parent_node, int siezeof_graph, int sizeof_mileage);
int findGraphNodeIndex(GRAPH *start_to_fin, char *node, int siezeof_graph);
int renewCost(GRAPH *start_to_fin, MILEAGE *shortest_mileage, PARENT *parent_node, int graph_index, int sizeof_mileage, int *visited);
int findMileageNodeIndex(char *name_node, MILEAGE *shortest_mileage, int sizeof_mileage);
void renewParent(char *name_graph, PARENT *parent_node, int index_mileage);

int main(void) {
  PATH START[] ={{"A", 6}, {"B", 2}}, A[] = {{"FIN", 1}}, B[] = {{"A", 3}, {"FIN", 5}}, FIN[] = {{0, 0}};
  GRAPH start_to_fin[] = {{"START", START, 2}, {"A", A, 1}, {"B", B, 2}, {"FIN", FIN, 0}};
  MILEAGE shortest_mileage[] = {{"A", MAX_INT}, {"B", MAX_INT}, {"FIN", MAX_INT}};
  PARENT parent_node[] = {{"A", ""}, {"B", ""}, {"FIN", ""}};
  int sizeof_mileage = sizeof(shortest_mileage)/sizeof(shortest_mileage[0]);
  findShortestPath(start_to_fin, shortest_mileage, parent_node, sizeof(start_to_fin)/sizeof(start_to_fin[0]), sizeof_mileage);
  for (int j = 0; j < sizeof_mileage; ++j) printf("total %s = %d, ", shortest_mileage[j].node, shortest_mileage[j].total);      //測試shortest_mileage
  printf("\n");
  for (int j = 0; j < sizeof_mileage; ++j) printf("%s'parent = %s, ", parent_node[j].node, parent_node[j].father);          //測試parent
  printf("\n");  
  return 0;
}

void findShortestPath(GRAPH *start_to_fin, MILEAGE *shortest_mileage, PARENT *parent_node, int siezeof_graph, int sizeof_mileage) {    //找最短路徑
  int graph_index = findGraphNodeIndex(start_to_fin, "START", siezeof_graph);
  int visited[sizeof_mileage];                                     //觀察節點是否使用過，序號對應graph_index，用過為1，沒用過為0
  for (int i = 0; i < siezeof_graph; ++i) visited[i] = 0;
  int visited_index = renewCost(start_to_fin, shortest_mileage, parent_node, graph_index, sizeof_mileage, visited);    //第一次更新shortest_mileage
  while (visited_index != sizeof_mileage-1) {                                                             //重複更新，直到FIN節點為未更新節點中的最低
    graph_index = findGraphNodeIndex(start_to_fin, shortest_mileage[visited_index].node, siezeof_graph);
    visited_index = renewCost(start_to_fin, shortest_mileage, parent_node, graph_index, sizeof_mileage, visited);
  }
}

int findGraphNodeIndex(GRAPH *start_to_fin, char *node, int siezeof_graph) {      //找出節點圖形中對應名子的序號
  for (int i = 0; i < siezeof_graph; ++i) {
    if (strcmp(start_to_fin[i].node, node) == 0) return i;
  }
  return -1;
}

int renewCost(GRAPH *start_to_fin, MILEAGE *shortest_mileage, PARENT *parent_node, int graph_index, int sizeof_mileage, int *visited) {
  int index_mileage_node = findMileageNodeIndex(start_to_fin[graph_index].node, shortest_mileage, sizeof_mileage);
  for (int i = 0; i < start_to_fin[graph_index].member; ++i) {
    int index_mileage = findMileageNodeIndex(start_to_fin[graph_index].graph_path[i].node, shortest_mileage, sizeof_mileage);  //找出對應節點並更新
    if (index_mileage_node == -1) {                                                                                       //檢查是否為shortest_mileage中的節點
      shortest_mileage[index_mileage].total = start_to_fin[graph_index].graph_path[i].distance;
      renewParent(start_to_fin[graph_index].node, parent_node, index_mileage);
    }
    else if (shortest_mileage[index_mileage].total > shortest_mileage[index_mileage_node].total + start_to_fin[graph_index].graph_path[i].distance) {
      shortest_mileage[index_mileage].total = shortest_mileage[index_mileage_node].total + start_to_fin[graph_index].graph_path[i].distance;   //要先找出對應graph_index的mileage_index
      renewParent(start_to_fin[graph_index].node, parent_node, index_mileage);
    }
  }
  // for (int j = 0; j <sizeof_mileage; ++j) printf("%s = %d, ", shortest_mileage[j].node, shortest_mileage[j].total);      //測試shortest_mileage
  // printf("\n");
  int shortest_distence = MAX_INT, mileage_index = 0;               
  for (int j = 0; j <sizeof_mileage; ++j) {                       //找出要刪除的節點
    if (shortest_distence > shortest_mileage[j].total && visited[j] == 0) {
      shortest_distence = shortest_mileage[j].total;
      mileage_index = j;
    }
  }
  visited[mileage_index] = 1;           //標記用過節點
  // for (int j = 0; j < sizeof_mileage; ++j) printf("visited %s = %d, ", shortest_mileage[j].node, visited[j]);          //測試visited
  // printf("\n");
  // for (int j = 0; j < sizeof_mileage; ++j) printf("parent %s = %s, ", parent_node[j].node, parent_node[j].father);          //測試parent
  // printf("\n");
  return mileage_index;
}

int findMileageNodeIndex(char *name_node, MILEAGE *shortest_mileage, int sizeof_mileage) {        //找出shortest_mileage中對應名子的序號
  for (int i = 0; i < sizeof_mileage; ++i) {
    if (strcmp(name_node, shortest_mileage[i].node) == 0) return i;
  }
  return -1;
}

void renewParent(char *name_graph, PARENT *parent_node, int index_mileage) {      //更新parent節點
  strcpy(parent_node[index_mileage].father, name_graph);
}

看更多先前的討論...收起先前的討論...

一級屠豬士 iT邦大師 1 級 ‧ 2023-10-23 19:25:26 檢舉

程式別擠一起,加點空白行.

shazbot001 iT邦新手 5 級 ‧ 2023-10-23 19:57:01 檢舉

謝回復。請容我解釋下，這程式碼在我的編譯器裡沒那麼擠，是這邊寬度較少，看起來才很壅擠。本來想說要不要貼程式碼圖片上來，方便別人閱讀；但想到有些人喜歡複製程式碼到自己的編譯器閱讀，而且貼程式碼比較方便別人複製。

codenoob iT邦新手 5 級 ‧ 2023-10-24 13:13:00 檢舉

其實可以用Github Gist把你的程式碼放在上面分享，也很好閱讀/複製程式碼

shazbot001 iT邦新手 5 級 ‧ 2023-10-24 14:00:40 檢舉

好，Github Gist我還沒用過，有空研究一下怎麼用。

登入發表討論

直播研討會

{{ item.channelVendor }} {{ item.webinarstarted }} |

直播中

1 個回答

淺水員

iT邦大師 6 級 ‧ 2023-10-26 20:27:58

下面程式碼用是物件的概念重寫過的
可以參考看看

#include <stdio.h>
#include <string.h>
#include <limits.h>

#define MAX_NODENAME 10
#define MAX_PATH 5

typedef struct path {
    struct node* node; // 路徑終點節點
    int distance; // 距離
} PATH;

typedef struct node {
    char name[MAX_NODENAME]; // 節點名稱
    PATH paths[MAX_PATH]; // 節點路徑陣列
    int path_count; // 節點路徑個數

    // 以下為計算過程使用
    int mileage; // 最短里程
    struct node* father; // 最短里程的父節點
    int visited; // 是否已經訪問
} NODE;

typedef struct graph {
    NODE* nodes; // NODE 陣列
    int node_count; // NODE 陣列的個數
    int start_index; // 起始點的 index
    int finish_index; // 終點的 index
} GRAPH;

NODE* getNodeByName(GRAPH* graph, const char* name);
int addPath(GRAPH* graph, const char* src, const char* dest, int distance);
void updateCost(NODE* node);
NODE* getMinMileageNode(GRAPH* graph);

int main(void)
{
    // 節點名稱
    const char* node_name_array[] = { "START", "A", "B", "FIN" };
    int node_count = sizeof(node_name_array) / sizeof(*node_name_array);

    // 初始化 node_collection（準備設定給 graph）
    NODE node_collection[node_count];
    for (int i = 0; i < node_count; ++i) {
        strcpy(node_collection[i].name, node_name_array[i]);
        node_collection[i].path_count = 0;
        node_collection[i].mileage = INT_MAX;
        node_collection[i].visited = 0;
        node_collection[i].father = NULL;
        node_collection[i].visited = 0;
    }

    // 圖
    GRAPH graph = { node_collection, node_count, 0, node_count - 1 };

    // 設定路徑
    addPath(&graph, "START", "A", 6);
    addPath(&graph, "START", "B", 2);
    addPath(&graph, "A", "FIN", 1);
    addPath(&graph, "B", "A", 3);
    addPath(&graph, "B", "FIN", 5);

    // 計算最短路徑
    graph.nodes[graph.start_index].mileage = 0;
    NODE* node = getMinMileageNode(&graph);
    while (node != NULL) {
        updateCost(node);
        node = getMinMileageNode(&graph);
    }

    // 輸出
    for (int i = 0; i < graph.node_count; ++i) {
        NODE* node = graph.nodes + i;
        printf("[%s] milleage = %d, parent = %s\n", node->name, node->mileage, node->father != NULL ? node->father->name : "(null)");
    }
    return 0;
}

NODE* getNodeByName(GRAPH* graph, const char* name)
{
    for (int i = 0; i < graph->node_count; ++i) {
        NODE* node = graph->nodes + i;
        if (strcmp(node->name, name) == 0) {
            return node;
        }
    }
    return NULL;
}

int addPath(GRAPH* graph, const char* src, const char* dest, int distance)
{
    NODE* node_src = getNodeByName(graph, src);
    NODE* node_dest = getNodeByName(graph, dest);
    if (node_src == NULL || node_dest == NULL) {
        return -1;
    }
    if (node_src->path_count >= MAX_PATH) {
        return -2;
    }
    PATH* path = node_src->paths + (node_src->path_count++);
    path->node = node_dest;
    path->distance = distance;
    return 0;
}

void updateCost(NODE* node)
{
    // 掃描此節點的路徑
    int src_node_mileage = node->mileage;
    for (int i = 0; i < node->path_count; ++i) {
        NODE* dest_node = node->paths[i].node;
        int distance = node->paths[i].distance;
        // 如果走此路徑的距離較短
        if (src_node_mileage + distance < dest_node->mileage) {
            // 更新目標節點的里程數與來源節點
            dest_node->mileage = src_node_mileage + distance;
            dest_node->father = node;
        }
    }
    node->visited = 1;
}

NODE* getMinMileageNode(GRAPH* graph)
{
    int minMilleage = INT_MAX;
    NODE* node = NULL;
    for (int i = 0; i < graph->node_count; ++i) {
        int mileage = graph->nodes[i].mileage;
        int visited = graph->nodes[i].visited;
        if (visited == 0 && mileage < minMilleage) {
            minMilleage = mileage;
            node = graph->nodes + i;
        }
    }
    return node;
}