題目來源 Best Time to Buy and Sell Stock II

問題
給一棵 二元樹，並回傳該 二元樹 的 中序走訪節點 的順序。
因為遞迴非常的明顯易懂，所以題目要求使用 iteratively 完成！

二元樹 定義:每個節點最多有兩個子樹的樹結構。( Wiki-二元樹 )
中序 定義:先訪問左樹，在訪問根，最後訪問右樹。( Wiki-中序(In-Order) )

題目給的二元樹的定義
public class TreeNode
{
public int val;
public TreeNode left;
public Tree right;

public TreeNode(int x)
{
this.val = x;
}
}

例子
給一棵樹
1
\
2
/
3

則要回傳 {1, 3, 2}
-> 其中序走訪就是反覆執行 左樹 -> root -> 右樹
訪問 root (1) 的 左樹 -> 為空
訪問 root(1), 並 輸出 1,
訪問 root(1) 的 右樹, 再從右樹的 root(2) 重覆同一步驟 左樹 -> root -> 右樹

想法
這題其實是課本上的題目，如果查看一下 wiki 答案就馬上找到了！
他主要的解法就是使用 Stack 來完成，而 Stack 主要的特性就是 先進後出。
所以我們可以利用 先進後出 把 root 先暫存著來達到中序走訪的目的。
假設我有一棵數如下：

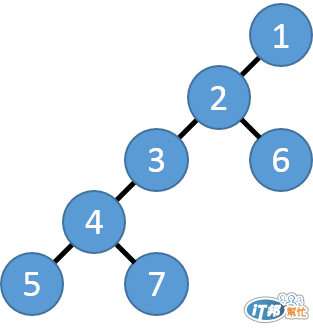
我就可以利用 stack 的特性操作如下：
將 root(1) 丟進 stack, 並訪問其左樹 stack[1]
將 root(2) 丟進 stack, 並訪問其左樹 stack[2 1]
將 root(3) 丟進 stack, 並訪問其左樹 stack[3 2 1]
將 root(4) 丟進 stack, 並訪問其左樹 stack[4 3 2 1]
將 root(5) 丟進 stack, 並訪問其左樹 stack[5 4 3 2 1]
此時 root(5) 的左樹為空, pop stack root(5), 並訪問其右樹 stack[4 3 2 1]
此時 root(5) 的右樹為空, pop stack root(4), 並訪問其右樹 stack[3 2 1]
將 root(7) 丟進 stack, 並訪問其左樹 stack[7 3 2 1]
此時 root(7) 的左樹為空, pop stack root(7), 並訪問其右樹 stack[3 2 1]
此時 root(7) 的右樹為空, pop stack root(3), 並訪問其右樹 stack[2 1]
此時 root(3) 的右樹為空, pop stack root(2), 並訪問其右樹 stack[1]
將 root(6) 丟進 stack, 並訪問其左樹 stack[6 1]
此時 root(6) 的左樹為空, pop stack root(6), 並訪問其右樹 stack[1]
此時 root(6) 的右樹為空, pop stack root(1), 並訪問其右樹 stack[1]

所以我們可以得到走訪的順序為 5 4 7 3 2 6 1

因此我們可以得到一個簡單演算法如下：

準備一個空的 Stack, 和一個指標指向 root
當 Stack不為空 或 指標指向的點不為null時
若 指標指向節點不為 null
push 節點
將指標指向左邊子節點
否則
pop stack
指標指向 pop 出來節點的右子節點

也就是說，一開始就是將 Left Child Push 進 Stack 中，直到沒有 Left Child 之後，就從 Stack 中 pop 出一個節點 （也就是剛剛最後 push 進去的 Left Child)，此時在 push 他的 Right Child。

如果該 Right Child 有 Left Child，則重複上面的步驟(push left child)繼續往下做。如果沒有在 Pop 出一個節點繼續做上面的步驟。直到 Stack 為空為止。

我們再以下面的樹為例子

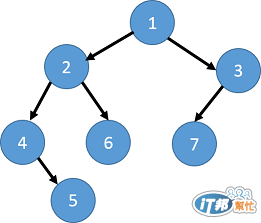
此數的走訪順序為：[4 5 2 6 1 7 3]

1. [Push left child] push 1, push 2, push 4 , (4 沒有左邊的子節點了)
2. pop 得到 4, push 5 (5 沒有左邊的子節點了)
3. pop 得到 5, (5 沒有右邊子節點)
4. pop 得到 2, push 6 (6 沒有左邊的子節點了)
5. pop 得到 6, (6 沒有右邊子節點)
6. pop 得到 1, push 3, push 7 ( 7 沒有左邊子節點 )
7. pop 得到 7, (7 沒有右邊子節點)
8. pop 得到 3 (stack 為空了 )

• 如果你用 C＃ 可以利用我的 測試程式 來驗證
• 如果你用 Java or Python or C++ 可上 LeetCode Online Judge 驗證
• 還是想不出來嗎？參考我的 解答(C#版本) 吧！

我的解答

public List<int> GetInorder(TreeNode root)
{
List<int> result = new List<int>();

Stack<TreeNode> bufferStack = new Stack<TreeNode>();
while (bufferStack.Count != 0 || root != null)
{
if (root != null)
{
bufferStack.Push(root);
root = root.left;
}
else
{
root = bufferStack.Pop();
result.Add(root.val);
root = root.right;
}
}

return result;
}