題目來源：Valid Binary Search Tree

問題
給一棵樹，判斷它是否是一棵合法的二元搜尋樹 (BST, Binary search tree)

關於 BST 的定義如下：

• 左子樹任一節點的值一定 小於 根(root) 的值
• 右子樹任一節點的值一定 大於 根(root) 的值
• 以上兩個條件會試用到當任一節點當 root

上面三點也就是在說明，在一棵BST中，任一節點的 值 一定

• 大於右子節點（包含該子節點的任一子孫節點）
• 小於左子節點（包含該子節點的任一子孫節點）

例子
例如下面這棵樹，他就是一棵合法的 BST (每一個節點都有符合 BST 的限制)

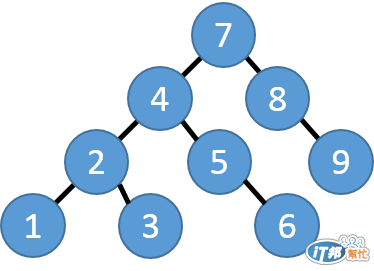
但下面這棵樹就不是一棵合法的 BST，因為節點 8 他大於 5 是合法，大於 4 也是合法的。但是，他不能大於 7 這個節點。畢竟 8 這個節點還是屬於 7 這個節點的左子樹。因此，他不是一棵合法的 二元搜尋樹 (BST)

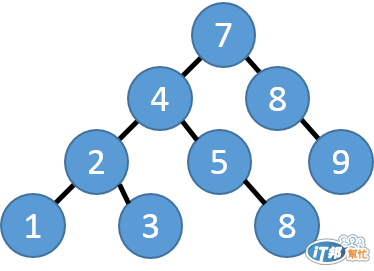
想法
這個題目乍看之下似乎好像有點不容易，如果採用比較的方式就會複雜一點點。因為必須要去比較 左子樹 要小於 根節點，接著在比較 右子樹 要大於 根節點。這樣就可以解開這個題目了。
但在這裡我不這麼做，我想要用另一種作法。
仔細想想，節點由小到大的排列順序是不是 左->中->右 呢？是不是感覺到有點熟悉？沒錯，就是在第五天提到的中序走訪。如果你也有發現這個規則，那這題就會變得非常容易！只要將一棵樹做中序走訪一遍，並且判斷 前一個節點 一定要小於 後一個節點 答案就出來了！

虛擬碼

準備一個 stack 和一個最小值還有一個節點指標
當 stack不為空 或 指標節點指向不為NULL
    若 指標指向節點不為NULL
        將該節點 push 進 stack
        將節點指標指向左子節點
    否則
        pop stack
        若 pop 出來的節點小於或等於 最小值
            則返回 此樹不是BST
        否則
            將最小值設定成剛 pop 出來節點的值
        指標節點指向 pop 出來節點的右子節點
返回 此樹為 BST        

• 如果你用 Java or Python or C++ 可上 LeetCode Online Judge 驗證

• 還是想不出來嗎？參考我的 解答吧！

  public boolean isValidBST(TreeNode root) {
  boolean isBST = true;
  Stack parentStack = new Stack();
  int minValue = Integer.MIN_VALUE;

   TreeNode node = root;
  
   while( !parentStack.isEmpty() || node != null){
       if (node != null){
           parentStack.add(node);
           node = node.left;
       } else {
           node = parentStack.pop();
           if (minValue >= node.val){
               isBST = false;
               break;
           } else {
               minValue = node.val;
           }
           node = node.right;
       }
   }
  
   return isBST;
  

  }