Finding Global Sum in logarithmic time 這是要把下面的陣列全部加起來的方法，必須在log時間內算出來！

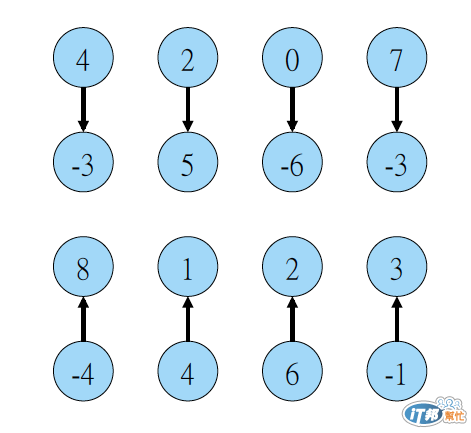
首先先做一回合的兩兩一組相加，

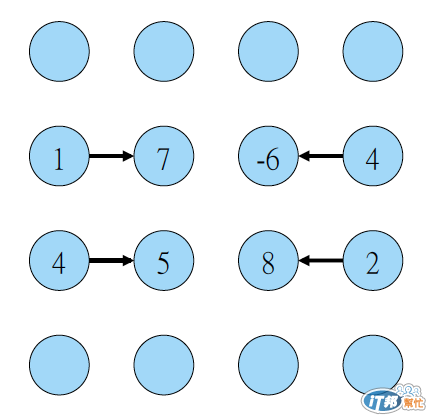
相加後的結果再做一回合的兩兩相加

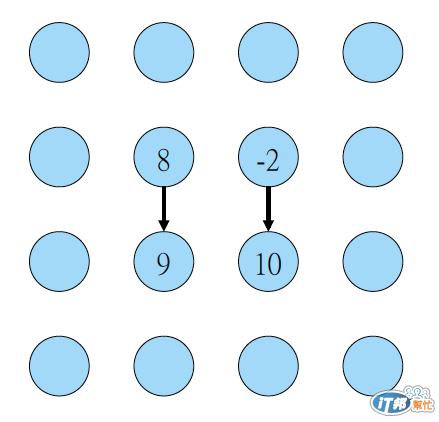
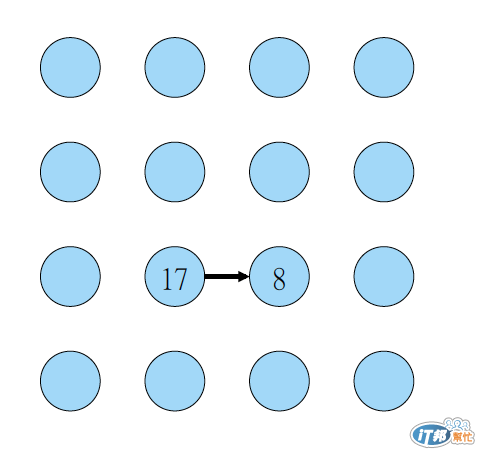
如此做法可在四回合算完 4x4 個元素

以二為底 log (16) = 4 回合

檢視一下我們做的步驟，觀察結果發現

其實左上，右上，左下，右下四個區塊等同於把區塊內的元素全部加起來的效果

這一步驟是做 Agglomeration整合 and Mapping 分配任務的結果

n tasks mapped to p processors

定義變數：n 個任務分配給 p 個處理器去做！

由上述的分析可得知

n/p primitive tasks

with 1 value

⇓

1 primitive tasks

with n/p values

這裡是在講 其實每區塊(四個task相加)整合後得到一個總和的結果

如此可把每四個一組的任務整合成一件單純的總和的任務

如此全部有 n = 16 個任務點，就整合成 (n/p) = (16/4) = 四件單純的總和的task得到一個總和的value

定義兩個變數

x 念做 "開" ：定義成做這個operation所需的時間，

入 念做"lamda" ：定義成訊息傳輸的延遲時間

如此：分給四個處理器同時運算時所花的時間為：

這裡是表示把(n/p) = (16/4) = 四個元素相加起來的任務運算

共需要做 4-1 = 3 次的相加。

而在做task之間的reduction整合的任務之中所需時間為

"lamda" 加 "開" ，意即訊息傳遞時間延遲加上做operation的時間

如此的p個處理器做p個task，整合時的任務共有 log p 個 communication steps

所以得到全部時間總和為：

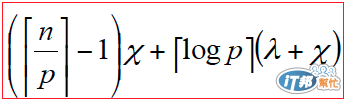
這裡好抽象... 希望大家不要覺得我在講外星語 ><