我們利用程式來計算機率時，在整條街的t%處開始拿起，同一個 t %跑10萬遍。會拿到最大值的機率(best)、一朵花都沒拿到的機率(fail)，以及雖然有拿到花，但沒有拿到最大值的機率(fine)
第一次在電腦上跑有種新奇感，跟爸爸做的事情一樣的感覺...有點爽...

跑出來會呈現下面這樣子，資訊的排列是：
時間, t 值,拿到最大值的機率（跑幾次log/總共球數log）

我將每個 t 值從 0 到 100 每次隔 0.1 共一千個值。總共 1000 顆球，跑 1,000,000 次，一個循環平均要跑約 58 秒，全部需要跑約 14 個小時。
最後得到的值傳送到表單裡，再做成圖表，最後變這樣：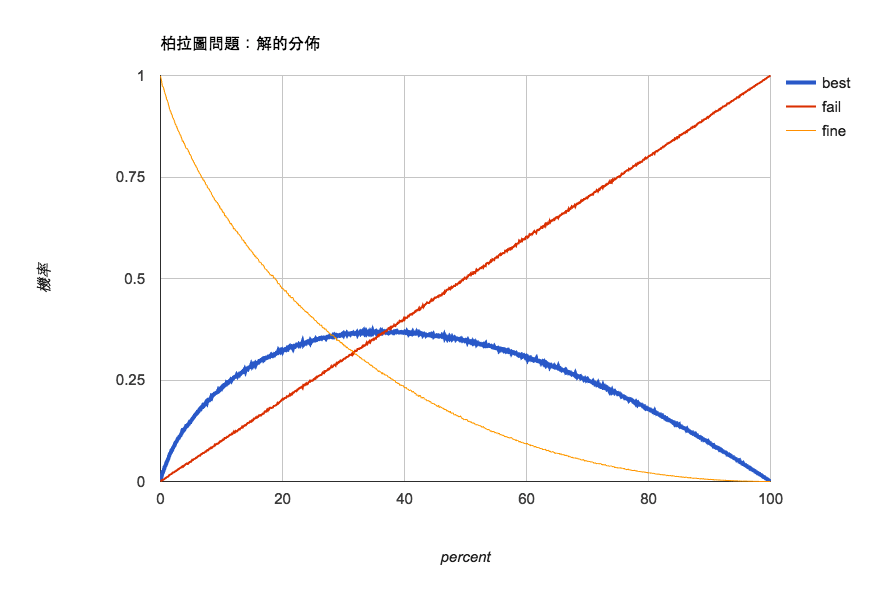

最後確實跟公式做出來的結論一致是在35%~40%（公式解為36.8…%）。程式成功！！

心得：
這是我第一次寫“真正”的程式，而且就直接拿來當報告了，說真的對我來說是一個大挑戰，我主要都是從爸爸那裡學來的，聽他講都一副超簡單的感覺，但我聽得超吃力...上一篇寫的程式有一些也是爸爸解救我的，一大堆的bug也是爸爸幫我修的...爸爸真的教我超多東西，不過接下來的東西不能再麻煩爸爸，加上這是我的科展，真的要自己把程式從頭到尾寫一遍了！！