最近幾天因為處在放鬆狀態，所以會對這個題目的東西亂想一通。我發現在第11篇關於工作效率的地方發現有另一件好玩的事可以加到這一個問題中，也就是「勸退辭職」。雖然大家都知道這樣並不是一件好的事情，不過重點是公司的利益啊（竊笑）～大概介紹一下問題：

如果你是蓋捷運的司令官，你必須要在三年內將一站捷運站蓋好。你必須要找到一位效率又高又快的工程師，越早動工越好。
很不幸的，在你發出應徵消息後的隔天，來了五十位工程師要應徵一份工作，於是你決定：為了正確評斷一個人，我一天只看一個人，只要我看到自己認為一位最好的工程師，我隔一天就叫他來指揮。
要怎要選擇員工才可以為工程達到最大效益呢？

在前一篇所說的結論發現：凋謝速率和工作效率是等價的。但是如果加上「反悔」這個變因呢？依照凋謝速率問題和工作效率問題的說法如下：

凋謝速率的說法：總共有十家店，花會隨著時間的流逝而凋謝，所以越後面的花分數會越來越低。拿到後你只能反悔一次，到最後只能拿取一朵花。
工作效率的說法：總共有十個員工要應徵，如果你要這位員工，隔天就可以叫他來工作。之後如果發現有更好的員工（一位），可以辭掉原本換上效率更高的員工。到最後也只能請一位。

但是有沒有發現，這兩個題目看似相同，但是有一個不同之處，也就是在反悔的地方。

在凋謝速率上，只要知道最後一家在結算分數就夠了，不會去管之前發生的任何狀況。但是在應徵問題上，只要有人在工作，工作總量就會持續上升。工作效率越高的人分數當然也會越加越大。之前的員工也是有工作的，所以也要將之前的所有工作量加上去。
以下面的圖做比喻好了：我在第4家拿到分數為5，但是到第七家時，發現分數居然比之前的都還要高為8，如下圖：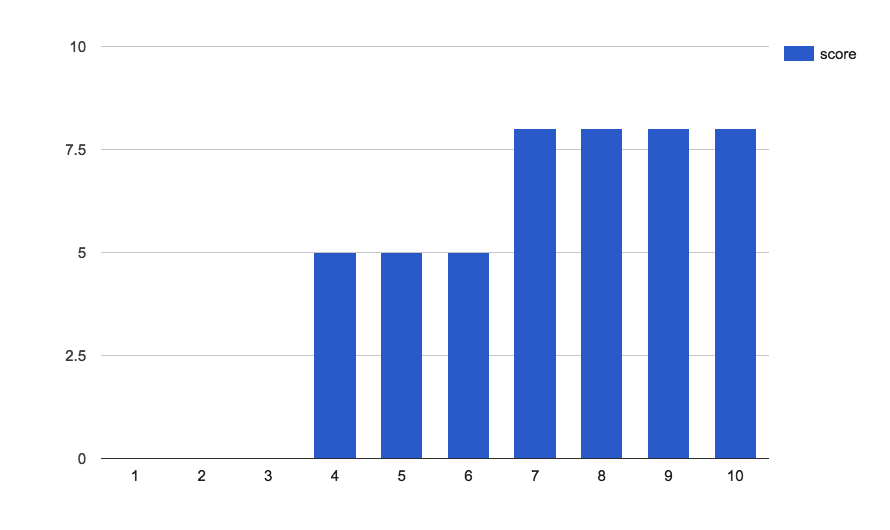

現在用不同的說法解釋這樣的情況：
凋謝：最後拿到的分數為8，為全部的8/10。
工作：分數為5的工作3天，分數為8的工作4天，總分是5x3+8x4=47，為全部的46/100。

結論：又有其他的變因可以做了～