前言

最近看書看到加解密相關的地方，運用指數和二進位特性來取得餘數和最大公因數和最小公倍數特性，在加解密上面都是相當重要的角色。

餘數相關原理

二進位

複習一下二進位的特性。
假設x = 9，
所以，

結果為1001，而在程式上面我們可以使用位移和AND才處理會比較快，應該有些人會疑惑為何會比較快，這次使用Visual Studio的反組譯來解釋。

位置：偵錯->視窗->反組譯(還有暫存器視窗可以看)。

主要看下圖綠色部分，num為無號，做除法前需先把餘數暫存器edx歸0(xor)，複製2到ecx暫存器(mov)，29除2(dev eax除ecx)，edx為32位元餘數的暫存，然而跟and相比and只需要一個步驟，所以通常運算時經常使用位元運算。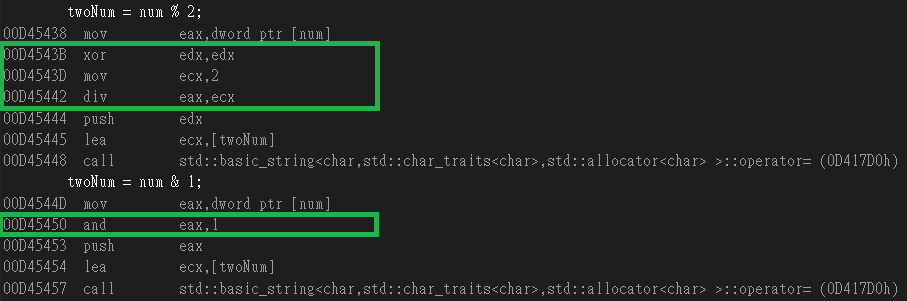

string GetTen2Two(unsigned int num)
{
	string twoNum = "";
	while (num > 0)
	{
		twoNum = (num & 1 ? "1" : "0") + twoNum;
		num >>= 1;
	}
	return twoNum;
}

指數

複習一下指數的特性。
指數的乘法：a^x1 * a^x2 = a^(x1 + x2) 。
這裡要多提到一個與二進位結合的特性。
例如，設x = 29，x的二進位為11101，
11101轉十進位 = 2^0 + 2^2 + 2^3 + 2^4 = 1 + 4 + 8 + 16 = 29。
假如我們要計算a^29，可分解為，a^1 * a^4 * a^8 * a^16 = a^29，接下來介紹的餘數將會使用這個特性。

餘數

分配公式。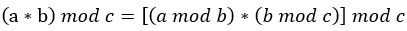
證明：
假設(除數 * 商 + 餘數)，
(a * b) = c * p1+ x1
a = c * p2 + x2
b = c * p3 + x3
所以，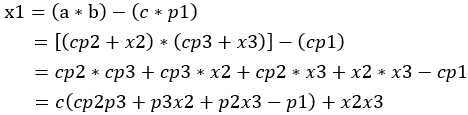
最後將x1的c(cp2p3 + p3x2 + p2x3 - p1)忽略，因為它是c的倍數必定餘數為0，最後只需計算(x2x3)的餘數，也就是a的餘數和b的餘數。

接下來剛剛提到的指數和二進位的特性 + 分配公式即可求到餘數，例如，572^29 mod 713，求餘數。
帶入剛才計算的572^1 * 572^4 * 572^8 * 572^16 = 572^29，再帶入分配公式，

1. 572^1 mod 713 = 572 mod 713。
2. 572^2 mod 713 = [(572^1 mod 713) * (572^1 mod 713)] mod 713。
3. 572^4 mod 713 = [(572^2 mod 713) * (572^2 mod 713)] mod 713。
4. 572^8 mod 713 = [(572^4 mod 713) * (572^4 mod 713)] mod 713。
5. 572^16 mod 713 = [(572^8 mod 713) * (572^8 mod 713)] mod 713。
   只需要(^1 * ^4 * ^8 * ^16) mod 713 就可以得到答案，這裡會發現可依二進位來乘，若當下位元是1就處理0則不處理。

#include <iostream>
#include <string>

using namespace std;

typedef unsigned int UINT;

// 十進位轉二進位
// Params:
// num: 數字
string GetTen2Two(UINT num)
{
	string twoNum = "";
	while (num > 0)
	{
		twoNum = (num & 1 ? "1" : "0") + twoNum;
		num >>= 1;
	}
	return twoNum;
}

// 取得餘數
// Params:
// num: 數字
// pow: 次方
// div: 除數
UINT GetRemainder(const UINT& num, UINT pow, const UINT& div)
{
	UINT remainder = 1;
	UINT powNum = num;
	while (pow > 0)
	{
		if (pow & 1)
		{
			remainder = (remainder * powNum) % div;
		}
		powNum = (powNum * powNum) % div;
		pow >>= 1;
	}
	return remainder;
}

int main()
{
	cout << GetTen2Two(29) << endl << GetRemainder(572, 29, 713) << endl;
	system("pause");
    return 0;
}

最大公因數

還記得國中所教的輾轉相除法求最大公因數嗎?，在數論當中它叫做歐幾里得演算法，接著來看公式。
公式，假設a >= b 則，a mod b = b mod (a mod b)....以此類推直到(a mod b) = 0則最大公因數為b。
證明:
使用餘商定理，假設c為a和b公因數，p為a / b的商，x為a mod b = x則a = p * b + x。
1.因為，c是a和pb的公因數。
2.反向用公倍數思考，假設a = c * n1，pb = c * n2，然而x = (a - pb) = c * (n1 - n2)。
3.所以，c也是x的公因數。

template<class T>
void Swap(T& t1, T& t2)
{
	T save = t1;
	t1 = t2;
	t2 = save;
}

// Params:
// num1: 數字a
// num2: 數字b
UINT GetFactor(UINT num1, UINT num2)
{
	if (num1 < num2)
	{
		Swap(num1, num2);
	}

	while (num2 > 0)
	{
		UINT remainder = num1 % num2;
		num1 = num2;
		num2 = remainder;
	}

	return num;
}

最小公倍數

最小公倍數算法可由最大公因數得來，公式為，最大公因數(a, b) * 最小公倍數(a, b) = a * b。
證明:
假設a = 30， b = 105，質因數分解為，a = 2 * 3 * 5，b = 3 * 5 * 7。
1.因為最大公因數為2^min(1, 0) * 3^min(1, 1) * 5^min(1, 1) * 7^min(0, 1) = 15，min為a和b對應指數。
2.最小公倍數為2^max(1, 0) * 3^max(1, 1) * 5^max(1, 1) * 7^max(0, 1) = 210，max為a和b對應指數。
3.所以，大公因數(a, b) * 最小公倍數(a, b) = a * b。

// Params:
// num1: 數字a
// num2: 數字b
// factor: 最大公因數
UINT GetMultiple(const UINT& num1, const UINT& num2, const UINT& factor)
{
	return num1 * num2 / factor;
}

// Params:
// num1: 數字a
// num2: 數字b
UINT GetMultiple(const UINT& num1, const UINT& num2)
{
	const UINT factor = GetFactor(num1, num2);
	return GetMultiple(num1, num2, factor);
}

模反元素

歐幾里得變形公式

在介紹模反元素時，若使用歐幾里得變形公式則會加快求模反元素的速度，公式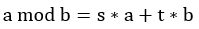，，在使用歐幾里得計算最後結果假設為3 mod 0 = 3 * 1 + 0 * 0 = 3，由此可知到最後一層是s = 1，t = 0，但我們需要計算的是第一層，若從第一層計算，必須知道這層和下層關西讓程式變的好寫(遞迴或迴圈跑到最後一個才一層一層往回傳)，所以先推導公式。
假設，。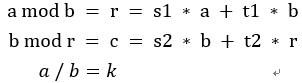
所以，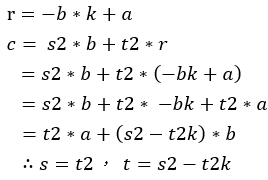

// Params:
// num1: 數字a
// num2: 數字b
// s: s * num1
// t: t * num1
UINT GetFactorSTRun(const UINT& num1, const UINT& num2, int& s, int& t)
{
	if (num2 == 0)
	{
		s = 1;
		t = 0;
		return num1;
	}

	int s2 = 0;
	int t2 = 0;
	const UINT remainder = num1 % num2;
	const UINT business = num1 / num2;
	const UINT factor = GetFactorSTRun(num2, remainder, s2, t2);

	s = t2;
	t = s2 - t2 * business;

	return factor;
}

// Params:
// num1: 數字a
// num2: 數字b
// s: s * num1
// t: t * num1
UINT GetFactorST(UINT num1, UINT num2, int& s, int& t)
{
	if (num1 < num2)
	{
		Swap(num1, num2);
		return GetFactorSTRun(num1, num2, t, s);
	}

	return GetFactorSTRun(num1, num2, s, t);
}

模反元素

若a和b互質(最大公因數1)，模反公式a * n mod b = 1，若0< n < b則n為a mod b的模反元素，使用歐幾里的變形公式推倒，a mod b = 1，變形公式為a * s + b * t = 1，移項 a * s = 1 - b * t，此時在這裡s正好符合n但要確保在0 < n < b，因此下面進一步推導。
假設n = s mod b(這裡若s為負，將s + b直到變正數)，k為商，此時已確保0 < n < b(歐幾里得證明s不等於0)。
因為，。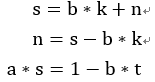
所以，。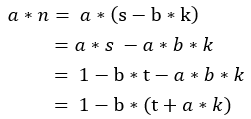
b乘上任何數都是0，所以必定餘1，推導為a * n mod b = 1。

歐拉定理

歐拉函數

公式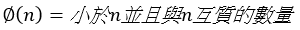，，若n是質數則歐拉函數為n - 1。

歐拉定理

公式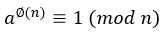，，這公式可用餘數算法的分配公式來證明，例如a = 3，n = 5，則3^5 mod 5 = 1，帶入分配公式[(3^1 mod 5) * (3^4 mod 5)] mod5...再把3^4也帶入分配公式以此類推，最後為1^5次方，所以可證歐拉定理公式a^∅(n) mod n = 1。
特性1，若a = p1 * p2，p1和p2互質，則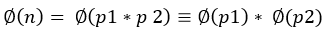，簡單解釋，當p1和p2互質時，∅(p1) = n1代表有n1種可能，∅(p2) = n2代表有n2種可能，則o(p1 * p2)有n1 * n2種可能，詳細數學推導參考中國剩餘定理[4]。

特性2，計算7^222 mod 10的餘數，因7和10互質，∅(10) = 4，故由歐拉定理可知 7^4 mod 10 = 1。所以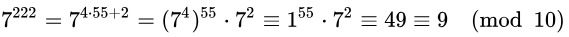
。取自維基百科範例[2]

RSA加解密

RSA由來，運用上面的公式可以製作一個"非對稱式加解密"的演算法，公鑰(z, n)加密公式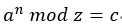，私鑰(z, s)加密公式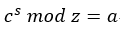。將a用公鑰加密為c傳送到伺服器，在使用私鑰解密，下面證明為何可當作加解密演算法。
假設，

• p1.p2為質數。
• z為p1 * p2。
• o為(p1 - 1) * (p2 - 1)(p1 * p2的歐拉數)。
• n * s mod o = 1，s為反元素。
• a為原始數據。
• c為加密後結果。

因歐拉公式a^∅(z) mod z = 1，歐拉特性2 [a^x1 * (a^∅(z))^x2] mod z = a^x1 mod z，反元素n * s mod z = 1。
帶入歐拉特性證明，a^(ns) mod z = 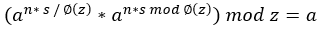，這裡用除法取得x2，結果一樣都是1，而n * s mod z = 1所以結果為1 * a^1。
使用餘數分配公式分成2部分變為，加密使用a^n mod z = c，解密使用c^s mod z = a。
註:加密的a必須比z小，因為它其實是一個對照表。

通常加密幾乎都用很大的數來去做，以下簡單實現：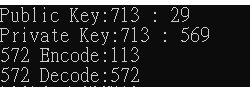

// Params:
// num1: 數字a
// num2: 數字b
UINT GetPrivateNum(const UINT& num1, const UINT& num2)
{
	int s = 0;
	int t = 0;
    // 用歐幾里得設定s
	GetFactorST(num1, num2, s, t);

	s = s < 0 ? num2 + s : s;
	return s;
}

// a^n mod z = c
UINT RSAEncode(const UINT& num, const UINT& z, const UINT& n)
{
	return GetRemainder(num, n, z);
}

// c^s mod z = a
UINT RSADecode(const UINT& num, const UINT& z, const UINT& s)
{
	return GetRemainder(num, s, z);
}

int main()
{
	const UINT p1 = 23;
	const UINT p2 = 31;
	const UINT n = 29;
	const UINT z = p1 * p2;
	const UINT o = (p1 - 1) * (p2 - 1);
	const UINT s = GetPrivateNum(n, o);
	const UINT encode = RSAEncode(572, z, n);
	const UINT decode = RSADecode(encode, z, s);

	cout << "Public Key:" << z << " : " << n << endl;
	cout << "Private Key:" << z << " : " << s << endl;
	cout << "572 Encode:" << encode << endl;
	cout << "572 Decode:" << decode << endl;

	system("pause");
	return 0;
}

結語

原本只要介紹最大公因數、最小公倍數和餘數，但最後想想只差一步就可能做加解密，於是就實作了簡單版的RSA加解密。書上對於歐拉沒有講解很多，但書上對於基礎的地方都還滿不錯的，若有錯誤地方歡迎指導討論。

參考文獻

[1]Richard Johnsonbaugh、吳世弘(譯者)（2011）。離散數學7e。台灣：華泰文化 。
[2]歐拉定理。檢自https://zh.wikipedia.org/wiki/%E6%AC%A7%E6%8B%89%E5%AE%9A%E7%90%86_(%E6%95%B0%E8%AE%BA)m (2018.08.24)。
[3]歐拉函數。檢自https://zh.wikipedia.org/wiki/%E6%AC%A7%E6%8B%89%E5%87%BD%E6%95%B0 (2018.08.24)。
[4]RSA歐拉定理。檢自http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html (2018.08.24)。