AI學習基礎

我們幾乎每天都會看到幾則有關『人工智慧(AI)』的新聞，一般人(me too!)都會想一窺究竟，了解箇中奧妙，但是，初次接觸，探究其原理，很多人就會被相關的數學/統計公式及符號所震攝，很快就鳴金收兵了，為了挽救蒼生(胡說八道的)，筆者想在這裡提出一個不算新的想法 -- 『以程式解決統計問題』(Statistical Programming)，換個角度想，我們是不是也能『以程式設計的方式學統計』。

圖片來源：Decision makers need more math

依『How much mathematics does an IT engineer need to learn...』一文，學習AI，我們至少要了解以下四個學科：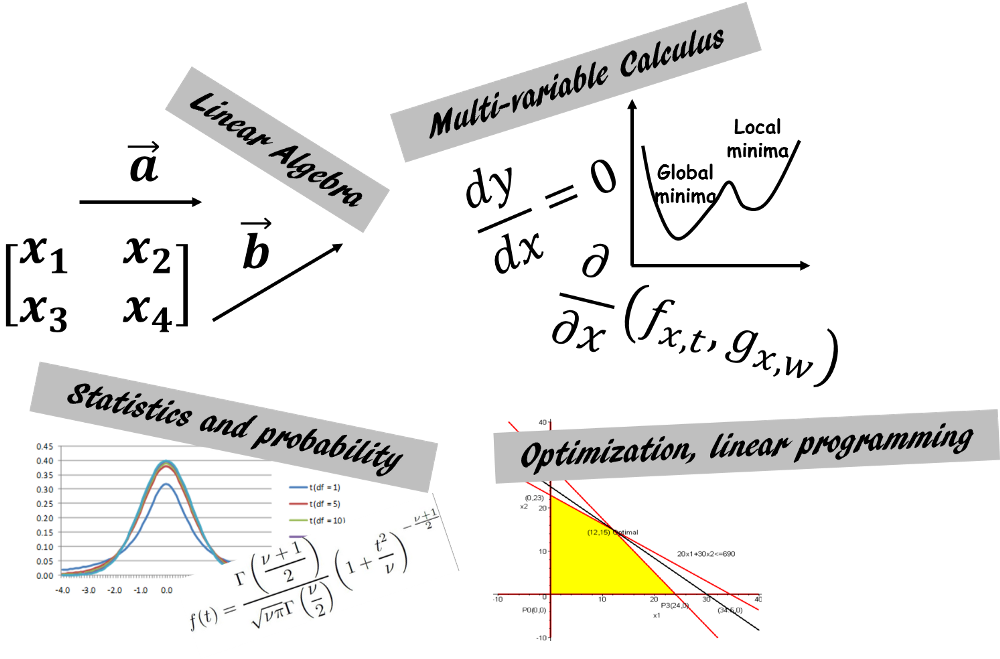

圖片來源：『How much mathematics does an IT engineer need to learn...』

1. 線性代數(Linear Algebra)
2. 微積分(Calculus)
3. 統計與機率(Statistics and Probability)
4. 線性規劃(linear programming)

以上四門課在大學至少都是兩學期的課程，加起來就是要修24個學分，對已經離開大學殿堂很久的工程師，應該會萌生退意了，因此，我們是不是有速成的捷徑呢? 囫圇吞棗總比餓肚子好，以下我們就來想想看吧。

以程式設計代替公式推導

要縮短學習路徑，先想想我們需要知道甚麼? 數學/統計都是從『假設』、『定義/定理』、『證明』、『應用/計算/檢定』一路學習下來：

• 『假設』說明『定義/定理』成立的前提。
• 『證明』驗證『定義/定理』是成立的。
• 『應用/計算/檢定』是『定義/定理』的實踐，或是假設的驗證。

從以上說明，工程師只要理解『假設』、『定義/定理』、『應用/計算/檢定』就夠了，至於，『證明』工作就留給科學家或數學家吧，因為『證明』都會有一堆的數學符號及公式推導，常會讓人頭暈腦脹。以下舉個簡單的範例說明『Statistical Programming』的概念，如有謬誤，就只能怪筆者才疏學淺，胡說八道了。

從斜率(Slope)到梯度下降(Gradient Descent)

我們知道『梯度下降法』(Gradient Descent)是深度學習優化求解最重要的關鍵，而『梯度』就是多元變數(Multi-Variates)的斜率，因此，我們就可以從『斜率』開始理解，下圖是一個簡單線性迴歸的圖解：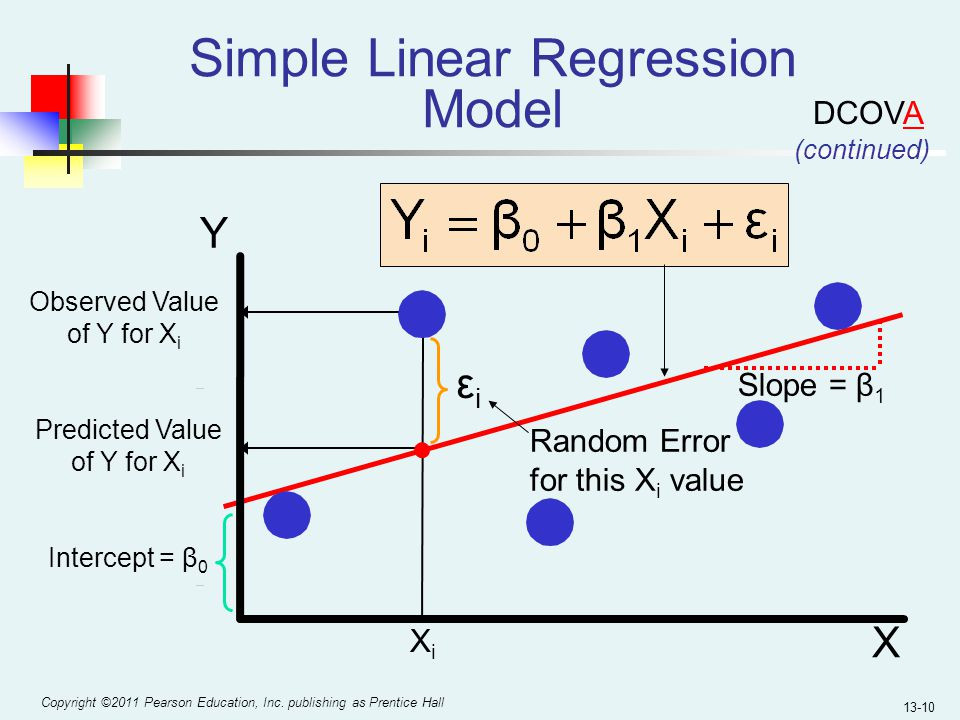

圖片來源：『Machine-Learning-with-Python』

簡單線性迴歸方程式如下
y=b1x+b0

其中 b1:斜率
b0:截距(intercept)或稱偏差(bias)

要求出迴歸線的斜率，我們就可以依據『最小平方法』(Ordinary Least Square, OLS)公式求出斜率：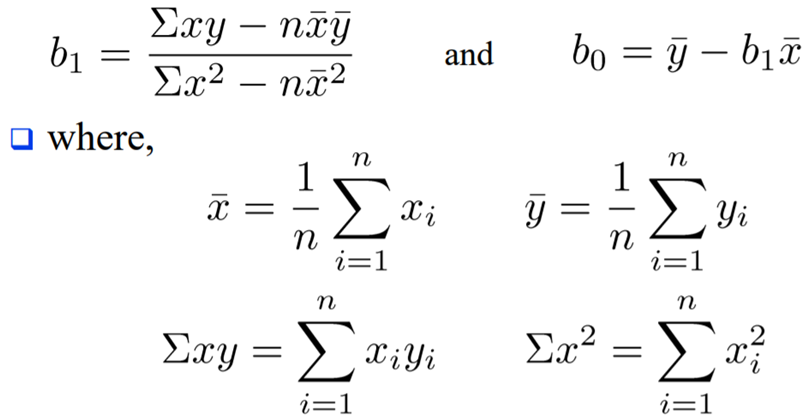

我們就單純以 Python 完成它吧：

# 方法1，單純用 Python
x = [0.0, 1.0, 2.0, 3.0,  4.0,  5.0]
y = [0.0, 0.8, 0.9, 0.1, -0.8, -1.0]

# x 平均數
x_mean = 0
for i in x:
    x_mean += i
x_mean = x_mean / len(x)

# y 平均數
y_mean = 0
for i in y:
    y_mean += i
y_mean = y_mean / len(y)

# x、y 乘積和
xy_sum = 0
for index, i in enumerate(x):
    xy_sum += i * y[index]

# x 平方和
x2_sum = 0
for i in x:
    x2_sum += i * i

# 斜率的分子
b1_numerator = (xy_sum - len(x) * x_mean * y_mean)
# 斜率的分母
b1_denominator = x2_sum - len(x) * x_mean * x_mean
# b1:斜率
b1 = b1_numerator / b1_denominator

# b0:截距
b0 = y_mean - b1 * x_mean

print('y={:.4f} x + {:.4f}\n'.format(b1, b0))

可以看到算出的迴歸方程式，並畫個圖，看看算的對不對。

import matplotlib.pyplot as plt
# 畫圖
plt.plot(x, b1 * np.array(x) + b0, color='red')
plt.scatter(x, y)
plt.show()

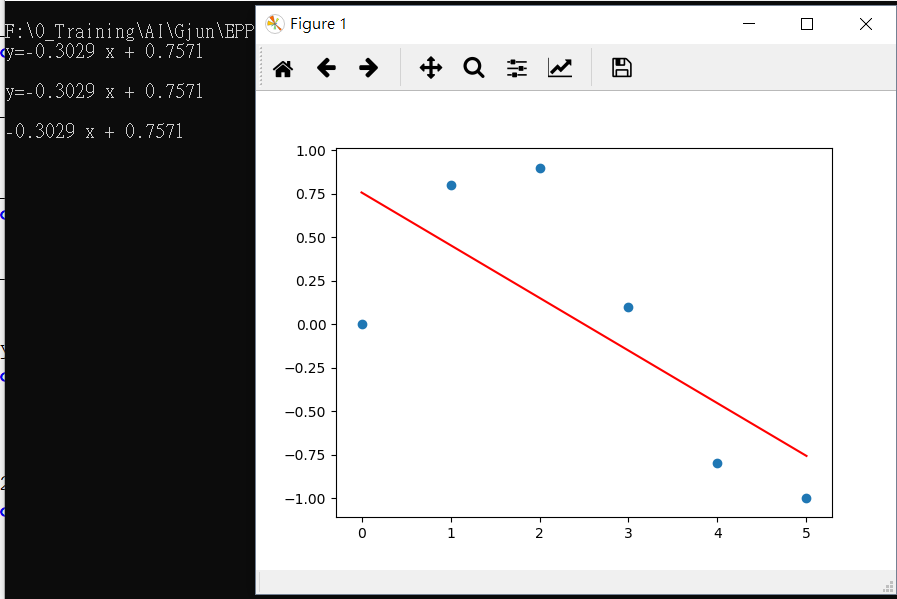
也可以使用現成的NumPy套件如下，比對一下答案。

import numpy as np
cls = np.polyfit(x, y, deg=1)
p = np.poly1d(cls)
print(p)

以上的程式撰寫及視覺化功能，比傳統的學習方法，有以下的優點：

1. 由圖形看，確實能說明公式是有效的。
2. 任意變換數據，我們的程式依然不變，可以解決問題。
3. 我們可以在圖形加註或製作簡單動畫(animation)，讓學習更生動活潑。
4. 除錯的過程可以讓我們檢視每一步驟計算的過程，使學習更深刻。
5. 將相關的函數製作成套件(Package)，可以逐步堆疊我們的知識。

結論

以上拉哩拉喳講了一堆，無非是希望藉由程式的撰寫，提高對數學/統計的理解，搜尋關鍵字『Statistical Programming』，其實可以找到很多相關的書籍，在此推薦一本與同好分享， 『Think Stats- Probability and Statistics for Programmers』，另外，OpenEdx 認證課程DAT256x 的 Lab 也是很好的教材，從線性方程式、聯立方程式求解、微分/積分、向量/矩陣/SVD、機率/統計，都有一淺顯的介紹，非常精彩。

了解簡單線性迴歸的概念後，下次我們就來進一步探討『梯度下降』，利用優化(Optimization)求解。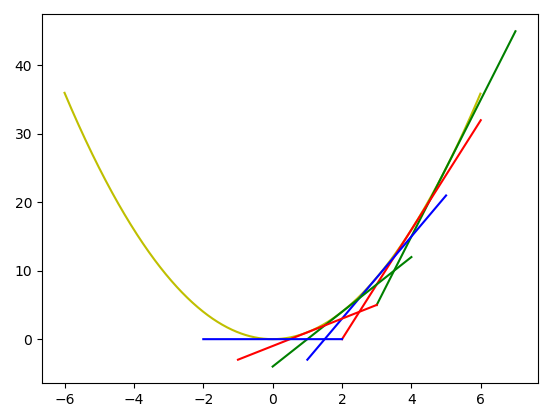

本文程式均放在 github 上歡迎取閱。