演算法的效率

在解題時給定輸入規模時常大的許多，一些 2 倍 3 倍 甚至 10 倍的優化其實不在演算法競賽時考慮的要點。
我們所設計的演算法必須根據輸入規模而定。

• Big O 表示法
  
  通俗的說，當 N 足夠大的時候，我們存在一正數 c 使得 c|g(N)| 大於等於 |f(N)|

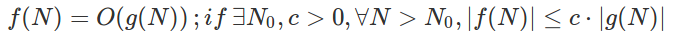
例如: f(x)= x^2 + x + 1 在 x 很大的時候，主要影響整個函數值的大小是平方項，這時我們可以說 f(x) = O(x^2)

假設輸入規模為 N，常見的複雜度有：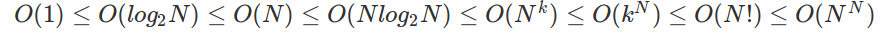

設計演算法的思維

這邊探討幾個常見去設計一個演算法的切入點

考慮最大連續和問題：
給定一個長度為 N 的整數數列 A[1], A[2], .. , A[n]，要求找到 1 <= i <= j <= n，使得 A[i] + A[i+1] + .. + A[j] 儘量大。

枚舉

所謂枚舉，通俗點說就是數出部份給定的集合中元素。
下面直接給出程式來解決最大連續和問題：

int best = A[1]; //與其用 int 最小值，不如這樣初始化更不易出錯

for (int i = 1; i <= N; i++)
  for (int j = i; j <= N; j++) {
    int sum = 0;
    for (int k = i; k <= j; k++) sum += A[k];
    best = max(best, sum);
  }

粗估一下可知道複雜度為 O(N^3)

練習：
GCJ Kickstart Round G 2018 A Product Triplets: Small dataset

動態規劃

部份朋友可能知道可以令 S[i] = A[1] + A[2] + ... A[i]
而 A[i] + A[i+1] + ... + A[j] = S[j] - S[i-1]
這樣子有了 S[i] 就可將連續和的計算從 O(N) 降為 O(1)

構造 S[i] 非常的直覺：

S[0] = 0;
for (int i = 1; i < N; i++) S[i] = S[i-1] + A[i];

從邊界遞推地紀錄所有問題的解，且一個項用到前一項的最佳結果，就是動態規劃的精神。

而程式可改進為：

for (int i = 1; i <= N; i++)
  for (int j = i; j <= N; j++) best = max(best, S[j] - S[i-1]);

複雜度降為 O(N^2)。

練習：
CODEFORCES 1033C Permutation Game

貪心法

貪心籠統的講，就是在做決策時，看到它可能是解，就認為它是解。
貪心法其實是動態規劃的特例，上面動態規劃恰好可以用貪心的角度去看，
即 每次 S[i] 所遞推拿的項 A[i]，正好不用任何考慮，疊上 S[i-1] 它就是解。

練習：
ZEROJUDGE d652 貪婪之糊
CODEFORCES 1065C Make It Equal

分治法

分治 (divide & conquer) 簡稱 D&C，就是將一個大的問題，分成幾個互相獨立的子問題，然後再將子問題分成子子問題，一直重複分割的動作，直到最小的問題足夠和別的最小問題合併求解出父問題。

將數列切一半，問左半的以及右半的最大連續和多少，以及問包含切開的那道分水嶺的最大連續和為多少，選出三者中最大值，它就是整個數列(原問題)的最大連續和：

int maxsum(int l, int r) {
  if (r-l == 1) return A[l];

  int m = (r+l)/2, sum, centre = A[m];

  sum = 0;
  for (int i = m  ; i <  r; i++) centre = max(centre, sum += A[i]);
  sum = centre;
  for (int i = m-1; i >= l; i--) centre = max(centre, sum += A[i]);

  return max(centre, max(maxsum(l, m), maxsum(m, r)));
}

其複雜度為 O(NlgN)
要驗證分治法的正確性，只需考慮子問題們解完後(假設已拿到解)，再合併為父問題看是否解完即可，還要考慮最小的孫子問題到的邊界是否正確。

今天先這樣，明天見！