閱讀前，建議可以參考Day1：閱讀指南＆為何選擇這個題目？

▌挑戰簡介

• 題目：計算機概論Ｘ30天

• 挑戰內容：連續30天紀錄計算機概論、離散數學、演算法、資料結構等課程，還有自己學習程式的心得體悟。

• 本篇性質：

  • 純粹學習內容的紀錄，不會有太嚴謹或是流暢的說明，所以看不太懂不是你智商的問題，請不要難過。
  • 介紹計算機底層如何用100101邏輯閘做「乘法」
  • 其實寫程式不用會這個沒關係

▌前情提要

根據前面的內容，我們已經學會如何使用「加法器」和「減法器」了。

現在就差一個乘法啦！！！

到底要怎麼做乘法呢？？

▌用左移（left Shift）乘以2

「乘法」用了一個我覺得很神奇的技巧——就是「左移」left Shift

比如說 0110 向左移(left shift)1 bit 變成 1100（最前面的0被幹掉了，110往左移，後面再補個0)

0110=6
1100=12

太神奇了傑克！只要往左移一個bit，就自動乘2了。

原理是什麼？因為愈靠左邊影響力愈大啊，然後11集體往左1個bit就變成2倍了。

再來一題

1111 = 15
往左shift left 1 bit ，ok答案，應該是30吧
1110 = 14 ....騙人!!怎麼會是14!!

其實沒有錯1110其實也可以等於是30喔！

30已經overflow了，根本不可能用4bit表達(畢竟4bit只能表達0~15)

但是在mod 16的情況下，30是等於14（也就是30=14 mod 16)

呃....意思就是說

原本0000~1111這16組號碼，是用來分配給0~15的。

但是假設我們硬是要16~31也分到號碼怎麼辦呢？

那只好...就還是分啊ＸＤ

於是就把0000~1111也分給16~31，讓16拿到0000，17拿到0001...因此類推

最後會發現

14 跟 30 分到的都會是同一組，也就是1110

15 跟 31 分到的也都是同一組，也就是1111

所以15 x 2是有成功的

▌用右移（right Shift）除以2

1010 = 10
然後往右移（right Shift）1 bit，也就是尾巴的0幹掉，前面的101往後退，最前端捕0
0101 = 5

太棒了！！得到5了！！

在一題
1001 =9
然後往右移（right Shift）1 bit，也就是尾巴的1幹掉，前面的100往後退，最前端捕0
0100 =4

... 呃 好像沒除以2...

對，在不能整除的情況下，這招不能work >.O

▌我要乘7怎麼辦

• 用左移（left Shift）可以乘以2
• 用右移（right Shift）可以除以2

可是教練，我要乘以7怎麼辦！

我要把3X7可以嗎？

可以，把3X7拆成3X2+3X2+3X2+3X1不就好ㄌ嗎

(1) 0011 X2 = 左移1bit= 0110
(2) 0011 X2 = 左移1bit= 0110
(3) 0011 X2 = 左移1bit= 0110
(4) 0011 X1 = 什麼都不要動 = 0011

3 = 0011（換成二進制）

OK 在加起來 0110+0110+0110+0011 = 0101

0101= 5

教練！騙人！根本就沒有變成21！

有啦ＱＱ

你看 5 = 21 mod 16 是相等的

因為21太大了啦，用4bit根本就裝不起來，所以勉為其難用0101表示了。

▌實作電路

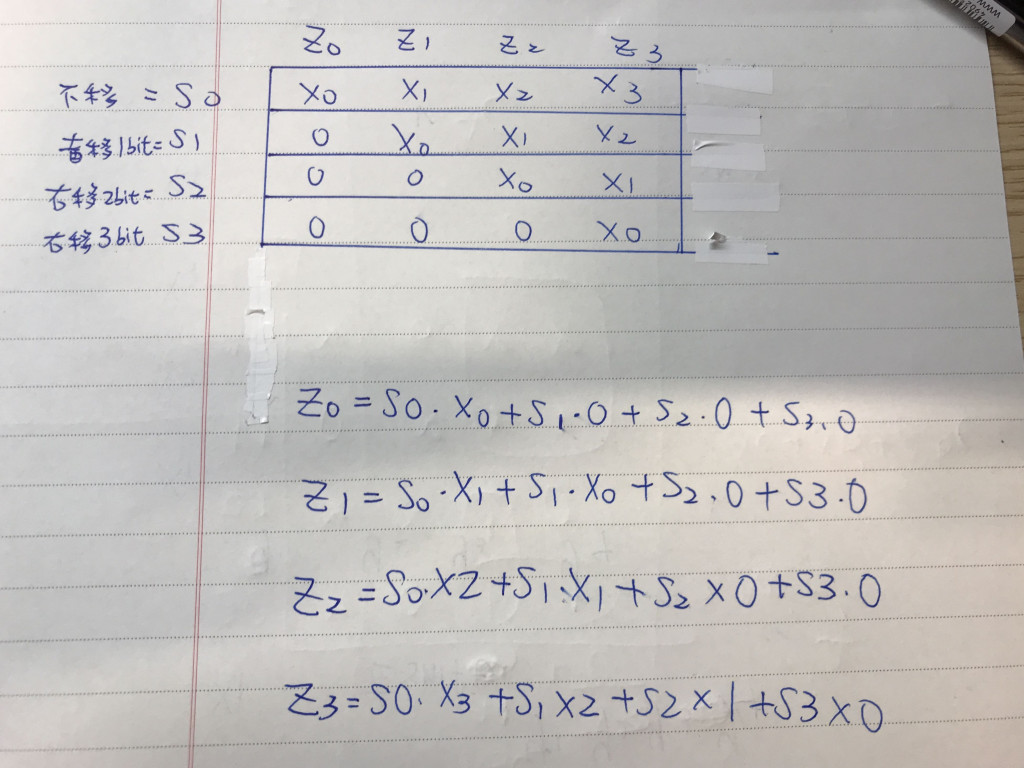
可以寫成類似truth table的東西，再用or/and之類的電路就可以串出來了

truth table太神啦！

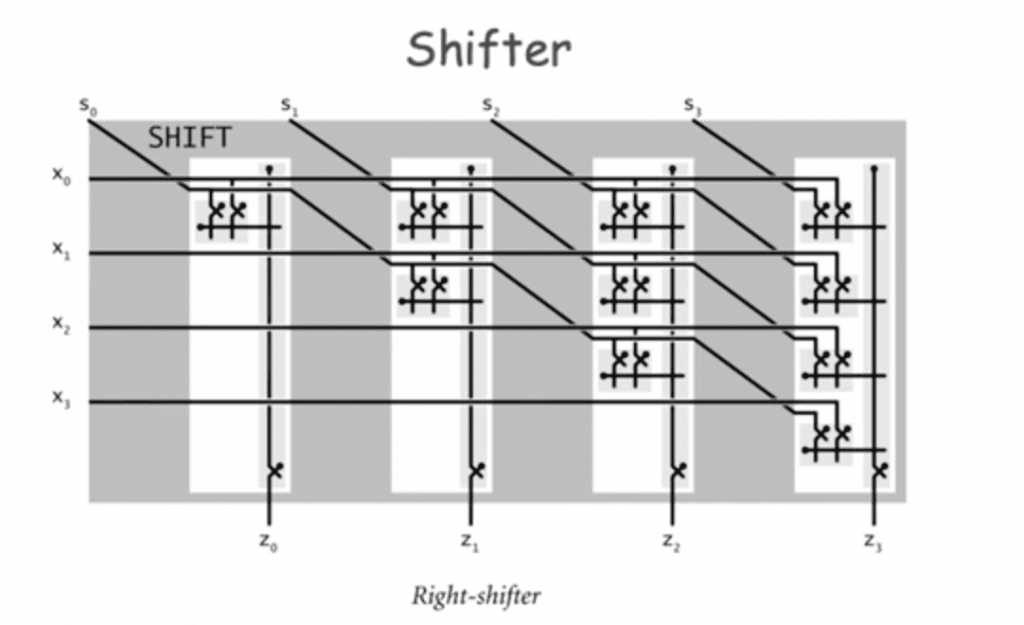
（看不懂很正常，我就是想放放圖）

▌心得

• 到底是誰想到用shift做乘法的？也太神奇了吧！