iT邦幫忙

0

[筆記]C++ & C#影像處理-邊緣檢測與霍夫轉換

c++ 影像處理 c#
Kevin 2018-11-22 16:58:34 ‧ 18384 瀏覽

前言

這次要介紹邊緣檢測和霍夫轉換一樣參考[1]，而邊緣檢測的Sobel為本次重點，因Sobel運算在往後取得方向和角度是非常方便的一個算式。

這次也修正了坐標和矩形相關的程式邏輯如下。

  • 矩形取得的endX和endY為實際索引位置，舉例endX公式為，x + width - 1，若width等於0回傳-1。
  • 矩形高度為實際高度。
  • 修正每個畫矩形有關的取得公式。
  • DrawLine8bit修正為自動換算畫出線。

邊緣運算子

簡介

[1]邊緣運算主要有Sobel、Scharr和Laplace，它們差異在於乘上的"核"不同，這裡使用Sobel中的3x3的一階核運算來當範例。

Sobel垂直方向3x3一階"核"：https://ithelp.ithome.com.tw/upload/images/20181121/20110564D7RGABc2O9.png。

Sobel水平方向3x3一階"核"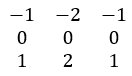：https://ithelp.ithome.com.tw/upload/images/20181121/20110564RKKg9SjkI4.png。

而垂直方向與水平方向計算出來結果映射在二維系座標，可以取得角度、方向和長度等等。假設垂直方向為x，水平方向為y，則依照三角函數性質可得到tan = 對邊 / 斜邊 = y / x，反三角函數atan則可得到角度，而距離公式使用歐幾里得距離公式(L2算法)，sqrt(x^2　+　y^2)，以上為合併後的性質，接著繼續看Sobel的運算步驟。

運算步驟

  1. 填補圖像。
  2. 取得核。
  3. 捲積處理。

程式碼

Library.h
這裡只使用一階3x3運算，dx和dy為使用開關。

	/*
		Sobel8bit Parameter:
		src			= source of image
		pur			= purpose of image
		width		= Image width
		height		= Image height
		dx			= x gradient switch
		dy			= y gradient switch
	*/
	void Sobel8bit(C_UCHAE* src, int32_t* pur
		, C_UINT32 width, C_UINT32 height
		, const bool dx, const bool dy);

Library.cpp

void Library::Sobel8bit(C_UCHAE* src, int32_t* data
	, C_UINT32 width, C_UINT32 height
	, const bool dx, const bool dy)
{
	// 1. padding
	C_UINT32 padWidth = width + 2;
	C_UINT32 padHeight = height + 2;
	UCHAE* padSrc = new UCHAE[padWidth * padHeight];

	ImagePadding8bit(src, padSrc, width, height, 1);


	// 2. set kernel
	Image srcImage(padSrc, padWidth, padHeight, MNDT::ImageType::GRAY_8BIT);
	int32_t kernels[9];

	SetSobelKernels(kernels
		, dx, dy);


	// 3. calculate convolution
	for (UINT32 row = 1; row < padWidth - 1; row++)
	{
		for (UINT32 col = 1; col < padHeight - 1; col++)
		{
			int32_t sum = 0;
			UINT32 kernelsIndex = 0;

			for (int32_t blockRow = -1; blockRow <= 1; blockRow++)
			{
				for (int32_t blockCol = -1; blockCol <= 1; blockCol++)
				{
					UCHAE pix = srcImage.image[row + blockRow][col + blockCol];

					sum += (static_cast<int32_t>(pix) * kernels[kernelsIndex]);
					kernelsIndex++;
				}
			}

			*data = sum;
			data++;
		}
	}

	delete[] padSrc;
	padSrc = nullptr;
}

結果圖

https://ithelp.ithome.com.tw/upload/images/20181121/20110564dkpkttnyY9.png
24bit垂直x

https://ithelp.ithome.com.tw/upload/images/20181121/20110564hjNIwjS0cq.png
24bit水平y

邊緣檢測

簡介

邊緣檢測主要是使用水平和垂直的絕對值(L1算法)合計後，再去做正規化顯示即是邊緣檢測。而邊緣檢測方式有很多種例如，Laplacian和Canny等等，但其原理大同小異，部分的差別只在於"核"的不同，這邊使用上述的Sobel運算子取得邊緣。

運算步驟

  1. 取得水平和垂直計算的Sobel值。
  2. 計算x和y絕對值的合，並取得目前最大值。
  3. 正規化將最大值轉為255。

程式碼

Library.h

	/*
		SobelEdgeView8bit Parameter:
		src			= source of image
		pur			= purpose of image
		width		= Image width
		height		= Image height
	*/
	void SobelEdgeView8bit(C_UCHAE* src, UCHAE* pur
		, C_UINT32 width, C_UINT32 height);

Library.cpp

void Library::SobelEdgeView8bit(C_UCHAE* src, UCHAE* pur
	, C_UINT32 width, C_UINT32 height)
{
	// 1. get sobel
	int32_t* Gx = new int32_t[width * height];
	int32_t* Gy = new int32_t[width * height];
	C_UCHAE* srcEnd = src + width * height;

	Sobel8bit(src, Gx
		, width, height
		, true, false);

	Sobel8bit(src, Gy
		, width, height
		, false, true);


	// 2. calculate abs and get max
	int32_t max = 0;
	int32_t* data = new int32_t[width * height];
	int32_t* dataPointer = data;
	int32_t* GxPointer = Gx;
	int32_t* GyPointer = Gy;

	while (src < srcEnd)
	{
		*dataPointer = abs(*GxPointer) + abs(*GyPointer);
		max = max < *dataPointer ? *dataPointer : max;

		dataPointer++;
		src++;
		GxPointer++;
		GyPointer++;
	}

	delete[] Gx;
	Gx = nullptr;

	delete[] Gy;
	Gy = nullptr;



	// 3. normalization
	C_UCHAE* purEnd = pur + width * height;
	dataPointer = data;

	while (pur < purEnd)
	{
		*pur = *dataPointer * 255 / max;

		dataPointer++;
		pur++;
	}

	delete[] data;
	data = nullptr;
}

結果圖

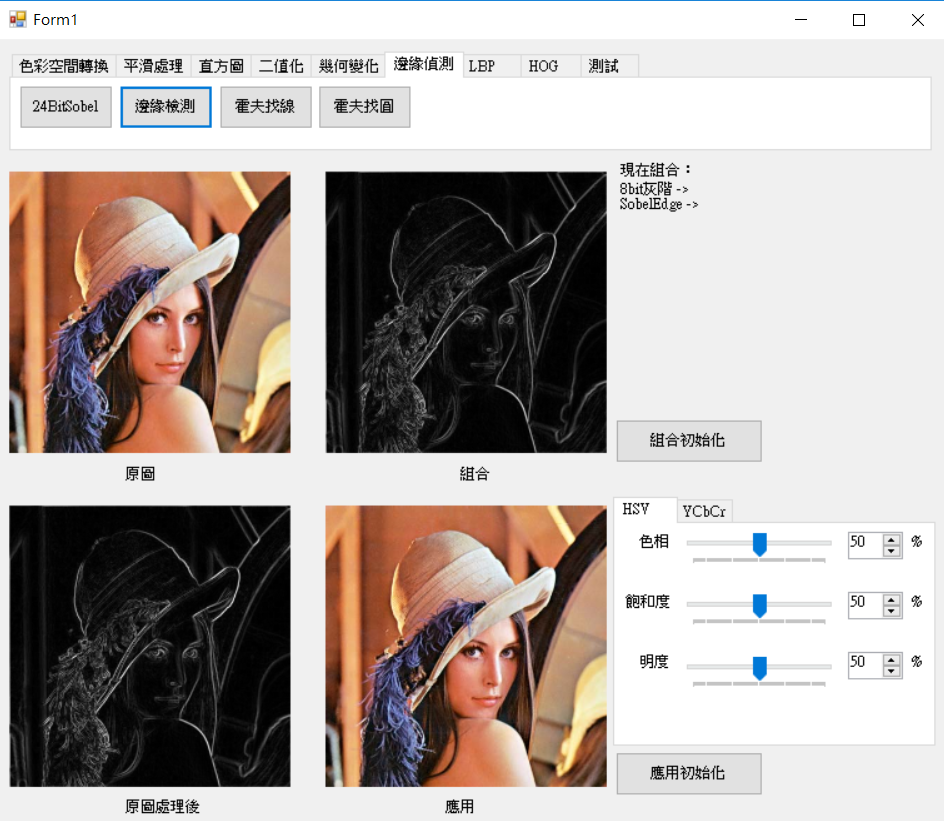
https://ithelp.ithome.com.tw/upload/images/20181121/20110564RHEDsOlDc6.png

霍夫找線

參考[2]的OpenCV代碼，主要將最後改為全部重新計算一次在畫出結果。

簡介

霍夫轉換是計算x和y在0~180角度的極座標(離散值)，使用三角函數cos　=　鄰邊　/　斜邊，sin　=　對邊　/　斜邊，而cos乘上斜邊得取x，sin乘上斜邊得取y，使用圖片的位置乘上cos和sin，cos(theta)　*　x取得x在霍夫分布和sin(theta)　*　y取得y分布，兩者相加即是霍夫轉換的離散值，如下圖一，圖二則是實際圖片輸出的分布有興趣可找函數DrawHoughPolar。

輸入資料[x, y]由上而下[7, 7], [5, 5], [3, 3], [1, 1]，可以清楚的看到都相交於弧度2.35(135度)位置，利用此特性統計直線的角度，將可能為直線的角度列出就可以減少計算量。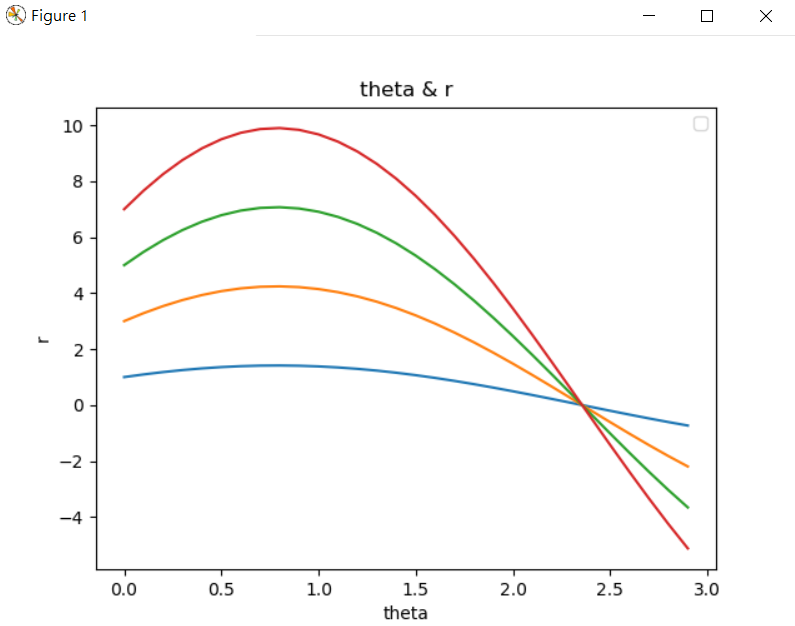
https://ithelp.ithome.com.tw/upload/images/20181121/20110564lV8ClM007j.png
圖一。

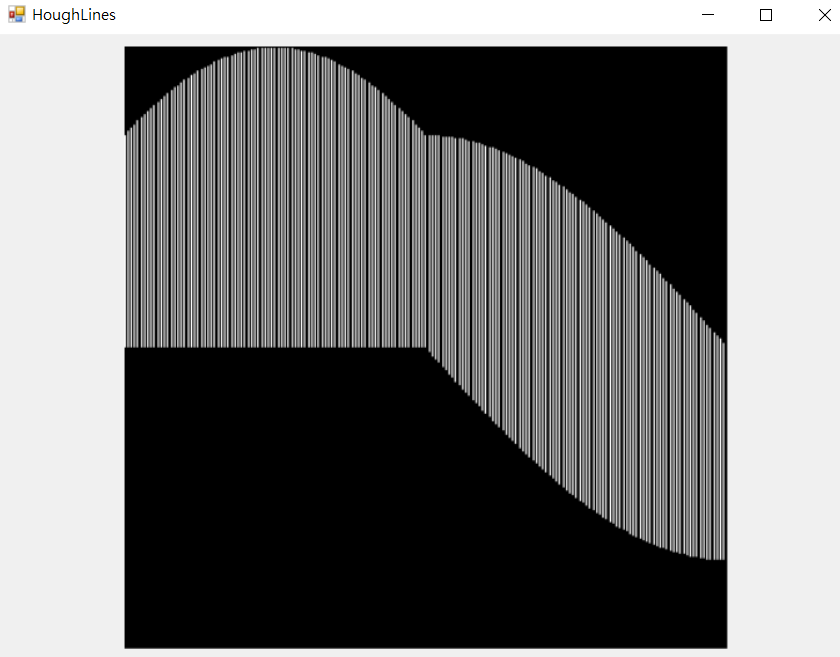
https://ithelp.ithome.com.tw/upload/images/20181121/201105641tXEK3VXhJ.png
圖二，整張圖片實際畫出的線。

初始化

  • thetaSize：分割數量。PI除theta，theta為每個切割弧度大小。
  • fixRho：三角函數倍率。1除rho，rho為倍率參數。
  • originalR：最大離散值。最大為長寬乘上0.7...(45度)或者高或寬乘上1。
  • maxR：修正的最大離散值。為了算鄰近，加上填補和修正索引位置。
  • xAxisOffset：負數的偏移位置。主要用來將離散值分為正和負兩部分，所以每一個分割角度的範圍是[-originalR,originalR]，。

運算步驟

  1. 初始化sin和cos的倍率與弧度分割數量。
  2. 像素大於0的座標做霍夫轉換，並且累加計算出來的離散位置。
  3. 使用四方鄰近法與上下左右的值比對，若該點可能是線則數值會比較大，若不是累加設為0。
  4. 像素大於0的座標做霍夫轉換，若累積不為0則輸出白色。(可以改為依照count數量排序後，依照取得前N個再去跑迴圈效率會較高)。

程式碼

Library.h

	/*
		HoughLines Parameter:
		src			= source of image
		pur			= purpose of image
		width		= Image width
		height		= Image height
		rho			= calculation sin and cos
		theta		= calculation split parmas
		threshold	= calculation output parmas
	*/
	void HoughLines(C_UCHAE* src, UCHAE* pur
		, C_UINT32 width, C_UINT32 height
		, C_FLOAT rho, C_FLOAT theta, C_UINT32 threshold);
        
	void HoughLineNeighboursUpdate(UINT32* count
		, C_UINT32 thetaSize, C_UINT32 maxR
		, C_UINT32 threshold);

Library.cpp

void Library::HoughLines(C_UCHAE* src, UCHAE* pur
	, C_UINT32 width, C_UINT32 height
	, C_FLOAT rho, C_FLOAT theta, C_UINT32 threshold)
{
	// 1. init params
	C_FLOAT fixRho = 1.0f / rho;
	C_UINT32 thetaSize = static_cast<UINT32>(MNDT::PI / theta);
	float* fixSin = new float[thetaSize];
	float* fixCos = new float[thetaSize];

	for (UINT32 index = 0; index < thetaSize; index++)
	{
		fixSin[index] = MNDT::FixValue(sin(theta * index)) * fixRho;
		fixCos[index] = MNDT::FixValue(cos(theta * index)) * fixRho;
	}

	// 2. hough total
	Image srcImage(const_cast<UCHAE*>(src), width, height, MNDT::ImageType::GRAY_8BIT);
	C_DOUBLE originalR = std::max((width + height) * sin(MNDT::PI / 4.0), static_cast<double>(std::max(width, height)));
	C_UINT32 maxR = static_cast<UINT32>(originalR * fixRho) + 1 + 2;
	C_UINT32 xAxisOffset = maxR * (thetaSize + 2);
	UINT32* count = new UINT32[xAxisOffset * 2]{ 0 };

	for (UINT32 row = 0; row < height; row++)
	{
		for (UINT32 col = 0; col < width; col++)
		{
			if (srcImage.image[row][col] > 0)
			{
				for (UINT32 index = 0; index < thetaSize; index++)
				{
					int32_t r = static_cast<int32_t>(fixSin[index] * row + fixCos[index] * col);

					r = r < 0 ? abs(r) + xAxisOffset : r;
					count[maxR * (index + 1) + r + 1]++;
				}
			}
		}
	}

	//// draw hough
	//DrawHoughPolar(pur
	//	, width, height
	//	, count
	//	, theta, maxR);

	// 3. update neighbours
	HoughLineNeighboursUpdate(count
		, thetaSize, maxR
		, threshold);


	// 4. draw line
	Image purImage(pur, width, height, MNDT::ImageType::GRAY_8BIT);

	for (UINT32 row = 0; row < height; row++)
	{
		for (UINT32 col = 0; col < width; col++)
		{
			if (srcImage.image[row][col] > 0)
			{
				for (UINT32 index = 0; index < thetaSize; index++)
				{
					int32_t r = static_cast<int32_t>(fixSin[index] * row + fixCos[index] * col);

					r = r < 0 ? abs(r) + xAxisOffset : r;
					if (count[maxR * (index + 1) + r + 1] > 0)
					{
						purImage.image[row][col] = 255;
					}
				}
			}
		}
	}

	delete[] fixSin;
	fixSin = nullptr;

	delete[] fixCos;
	fixCos = nullptr;

	delete[] count;
	count = nullptr;
}

void Library::HoughLineNeighboursUpdate(UINT32* count
	, C_UINT32 thetaSize, C_UINT32 maxR
	, C_UINT32 threshold)
{
	// 4鄰比較
	C_UINT32 xAxisOffset = maxR * (thetaSize + 2);

	for (UINT32 index = 0; index < thetaSize; index++)
	{
		C_UINT32 offset = maxR * (index + 1);

		for (UINT32 countIndex = offset + 1; countIndex < offset + maxR - 1; countIndex++)
		{
			// x axis -> + and -
			for (UINT32 axis = 0; axis < 2; axis++)
			{
				UINT32* nowCountPointer = count + countIndex + xAxisOffset * axis;

				if (*nowCountPointer < threshold
					|| *nowCountPointer < *(nowCountPointer - 1)
					|| *nowCountPointer < *(nowCountPointer + 1)
					|| *nowCountPointer < *(nowCountPointer - maxR)
					|| *nowCountPointer < *(nowCountPointer + maxR))
				{
					*nowCountPointer = 0;
				}
			}

		}
	}
}

https://ithelp.ithome.com.tw/upload/images/20181122/20110564uDu3TsosB5.jpg
原圖

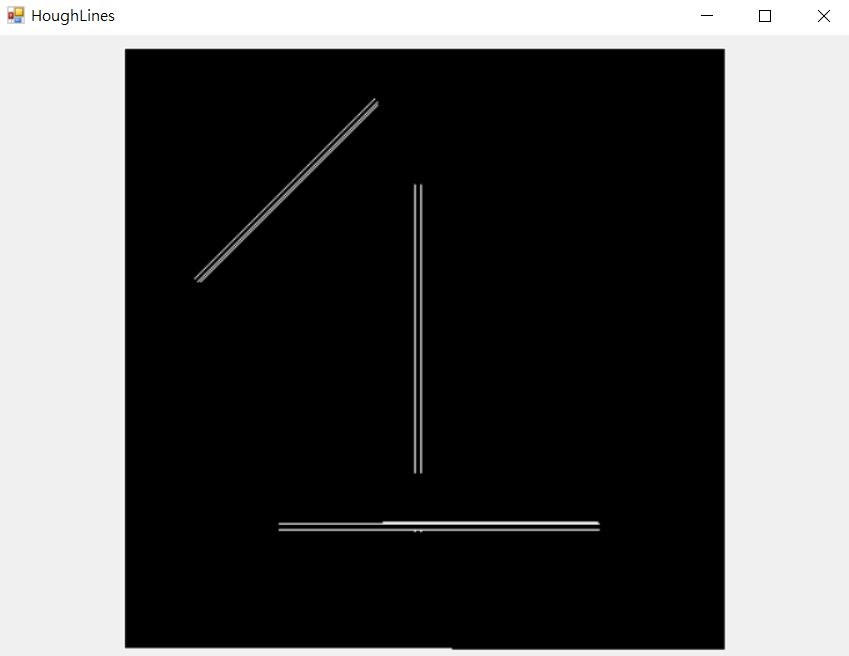
https://ithelp.ithome.com.tw/upload/images/20181122/20110564Qujq3UvP8O.png
結果

霍夫找圓

參考[3]的OpenCV代碼，在用更直觀方式實現。

簡介

圓的方式與直線相同，公式改為，r^2　=　x^2　+　y^2，而在OpenCV當中先統計有可能為圓心的位置，在去判別哪些是真正的圓心。首先找到大於0的像素，依照Sobel運算可取得梯度，而在這裡的梯度方向即是切線的法線(與切線垂直)，如此一來只需要往梯度方向和反方向累加通過的可能圓心點即可，如下圖一原圖，圖二為累加的所有路徑。

https://ithelp.ithome.com.tw/upload/images/20181122/201105642eawZa4Dqw.jpg
圖一

https://ithelp.ithome.com.tw/upload/images/20181122/20110564Oj56u73wAy.png
圖二

運算步驟

  1. 計算垂直x和水平y的Sobel運算子。
  2. 使用L2正規化梯度偏移量，使用count陣列統計像素大於0從minRadius到maxRadius經過的直線。這裡多用一個函數計算點到點之間經過的距離。
  3. 使用四方鄰近法與上下左右的值比對，若該點可能是線則數值會比較大，若不是累加設為0。
  4. count大於0的座標從minRadius到maxRadius判斷360度的位置是否為大於0的像素，若360度都是即是原心。(可以改為依照count數量排序後，依照取得前N個再去跑迴圈效率會較高)。

程式碼

Library.h

	/*
		HoughCircles Parameter:
		src			= source of image
		pur			= purpose of image
		width		= Image width
		height		= Image height
		minRadius	= min radius
		maxRadius	= max radius
		threshold	= calculation output parmas
	*/
	void HoughCircles(C_UCHAE* src, UCHAE* pur
		, C_UINT32 width, C_UINT32 height
		, C_FLOAT minRadius, C_FLOAT maxRadius, C_UINT32 threshold);
        
    	void HoughCirclesCount(C_UCHAE* src
		, C_UINT32 width, C_UINT32 height
		, UINT32* count
		, C_FLOAT minRadius, C_FLOAT maxRadius);

	void HoughCirclePointCount(UINT32* count
		, C_UINT32 width
		, const Point& p1, const Point& p2);

	void HoughCircleNeighboursUpdate(UINT32* count
		, C_UINT32 width, C_UINT32 height
		, C_UINT32 threshold);

Library.cpp

void Library::HoughCircles(C_UCHAE* src, UCHAE* pur
	, C_UINT32 width, C_UINT32 height
	, C_FLOAT minRadius, C_FLOAT maxRadius, C_UINT32 threshold)
{
	// 1. total
	UINT32* count = new UINT32[(width + 2) * (height + 2)]{ 0 };

	HoughCirclesCount(src
		, width, height
		, count
		, minRadius, maxRadius);


	// 2. update neighbours
	HoughCircleNeighboursUpdate(count
		, width, height
		, threshold);

	// 3. draw
	Image srcImage(const_cast<UCHAE*>(src), width, height, MNDT::ImageType::GRAY_8BIT);
	Image purImage(pur, width, height, MNDT::ImageType::GRAY_8BIT);

	for (UINT32 row = 0; row < height; row++)
	{
		C_UINT32 rowIndex = (row + 1) * width;

		for (UINT32 col = 0; col < width; col++)
		{
			C_UINT32 nowIndex = rowIndex + col + 1;

			if (count[nowIndex] == 0)
			{
				continue;
			}

			for (float radius = minRadius; radius <= maxRadius; radius++)
			{
				bool nCircle = false;

				for (float pi = 0; pi <= MNDT::PI * 2; pi += 0.2f)
				{
					int32_t y = static_cast<int32_t>(static_cast<float>(row) + MNDT::FixValue(sin(pi)) * radius);
					int32_t x = static_cast<int32_t>(static_cast<float>(col) + MNDT::FixValue(cos(pi)) * radius);

					if (x < 0 || y < 0
						|| (unsigned)x >= width || (unsigned)y >= height
						|| srcImage.image[y][x] == 0)
					{
						nCircle = true;
						break;
					}
				}

				if (nCircle)
				{
					continue;
				}

				for (float pi = 0; pi <= MNDT::PI * 2; pi += 0.2f)
				{
					C_UINT32 y = static_cast<UINT32>(row + MNDT::FixValue(sin(pi)) * radius);
					C_UINT32 x = static_cast<UINT32>(col + MNDT::FixValue(cos(pi)) * radius);

					purImage.image[y][x] = 255;
				}
			}
		}
	}

	delete[] count;
	count = nullptr;
}

void Library::HoughCirclesCount(C_UCHAE* src
	, C_UINT32 width, C_UINT32 height
	, UINT32* count
	, C_FLOAT minRadius, C_FLOAT maxRadius)
{
	assert(count != nullptr);

	// get gradient
	Library lib;
	int32_t* Gx = new int32_t[width * height];
	int32_t* Gy = new int32_t[width * height];

	lib.Sobel8bit(src, Gx
		, width, height
		, true, false);

	lib.Sobel8bit(src, Gy
		, width, height
		, false, true);

	// calculate gradient total
	Image srcImage(const_cast<UCHAE*>(src), width, height, MNDT::ImageType::GRAY_8BIT);

	for (UINT32 row = 0; row < height; row++)
	{
		C_UINT32 rowIndex = row * width;

		for (UINT32 col = 0; col < width; col++)
		{
			C_UINT32 index = rowIndex + col;

			if (srcImage.image[row][col] > 0)
			{
				C_FLOAT magnitude = static_cast<float>(sqrt(Gx[index] * Gx[index] + Gy[index] * Gy[index] + 0.0001f));
				float offsetX = Gx[index] / magnitude;
				float offsetY = Gy[index] / magnitude;

				for (UINT32 sign = 0; sign < 2; sign++)
				{
					float x = col + minRadius * offsetX;
					float y = row + minRadius * offsetY;

					for (float radius = minRadius; radius <= maxRadius; radius++)
					{
						if (x < 0 || y < 0
							|| x >= width || y >= height)
						{
							continue;
						}
						//MNDT::DrawLine8bit(purImage, Point(col, row), Point(static_cast<UINT32>(x), static_cast<UINT32>(y)));
						HoughCirclePointCount(count, width, Point(col, row), Point(static_cast<UINT32>(x), static_cast<UINT32>(y)));
						x += offsetX;
						y += offsetY;
					}

					offsetX = -offsetX;
					offsetY = -offsetY;
				}
			}
		}
	}

	delete[] Gx;
	Gx = nullptr;

	delete[] Gy;
	Gy = nullptr;
}

void Library::HoughCirclePointCount(UINT32* count
	, C_UINT32 width
	, const Point& p1, const Point& p2)
{
	C_UINT32 absDiffX = abs(static_cast<int32_t>(p1.X()) - static_cast<int32_t>(p2.X()));
	C_UINT32 absDiffY = abs(static_cast<int32_t>(p1.Y()) - static_cast<int32_t>(p2.Y()));
	C_UINT32 base = absDiffX > absDiffY ? absDiffY : absDiffX;
	C_INT32 diffX = static_cast<int32_t>(p1.X()) - static_cast<int32_t>(p2.X());
	C_INT32 diffY = static_cast<int32_t>(p1.Y()) - static_cast<int32_t>(p2.Y());
	C_INT32 baseX = diffX < 0 ? 1 : -1;
	C_INT32 baseY = diffY < 0 ? 1 : -1;

	int32_t x = p1.X();
	int32_t y = p1.Y();

	for (UINT32 index = 0; index < base; index++)
	{
		count[static_cast<UINT32>(static_cast<UINT32>(y + 1) * width + x + 1)]++;
		x += baseX;
		y += baseY;
	}
}


void Library::HoughCircleNeighboursUpdate(UINT32* count
	, C_UINT32 width, C_UINT32 height
	, C_UINT32 threshold)
{
	// 4鄰比較
	for (UINT32 row = 0; row < height; row++)
	{
		C_UINT32 rowIndex = (row + 1) * width;

		for (UINT32 col = 0; col < width; col++)
		{
			C_UINT32 nowIndex = rowIndex + col + 1;
			UINT32* nowCountPointer = count + nowIndex;

			if (*nowCountPointer < threshold
				|| *nowCountPointer < *(nowCountPointer - 1)
				|| *nowCountPointer < *(nowCountPointer + 1)
				|| *nowCountPointer < *(nowCountPointer - width - 2)
				|| *nowCountPointer < *(nowCountPointer + width + 2))
			{
				*nowCountPointer = 0;
			}
		}
	}
}

結果圖

https://ithelp.ithome.com.tw/upload/images/20181122/20110564uDu3TsosB5.jpg
原圖

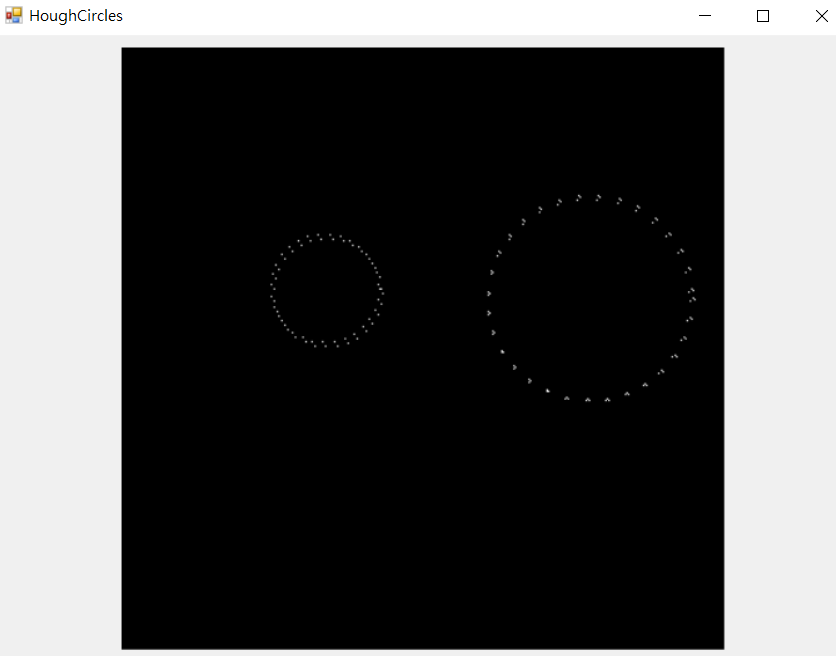
https://ithelp.ithome.com.tw/upload/images/20181122/20110564WQ0OoUhLK5.png
結果圖

結語

這次做的霍夫轉換直接把全部的可能輸出效率會較差，但對於理解原理沒有太大的影響。在[1]有提到分水嶺算法它是利用邊緣製作出一個標記表，再利用像素差進行合併，由此可知Sobel運算子運用的地方非常廣泛，接下來會介紹影像特徵取得，希望在月底能把AdaBoost做完/images/emoticon/emoticon06.gif。若有問題或錯誤歡迎留言指教。

C#視窗原始碼
C++函數原始碼

參考文獻

[1]阿洲(2015). OpenCV教學 | 阿洲的程式教學 from: http://monkeycoding.com/?page_id=12 (2018.11.21).
[2]viewcode(2012) 霍夫变换直线检测houghlines及opencv的实现分析 from: https://blog.csdn.net/viewcode/article/details/8090932 (2018.11.21).
[3]zhaocj(2016). Opencv2.4.9源码分析——HoughCircles from: https://blog.csdn.net/zhaocj/article/details/50454847 (2018.11.22)


圖片
  直播研討會
圖片
{{ item.channelVendor }} {{ item.webinarstarted }} |
{{ formatDate(item.duration) }}
直播中

尚未有邦友留言

立即登入留言

相關文章

iThome鐵人賽
參賽組數
1123 組
團體組數
52 組
累計文章數
23096 篇
完賽人數
656 人
iT+看影片追技術 看影片追技術 看更多
熱門tag 看更多
15th鐵人賽 13th鐵人賽 14th鐵人賽 12th鐵人賽 11th鐵人賽 鐵人賽 2019鐵人賽 2018鐵人賽 javascript 2017鐵人賽 python windows php c# windows server linux css react 程式設計 vue.js
熱門問題
熱門回答
熱門文章
IT邦幫忙