線段交叉判斷方法

線性函數

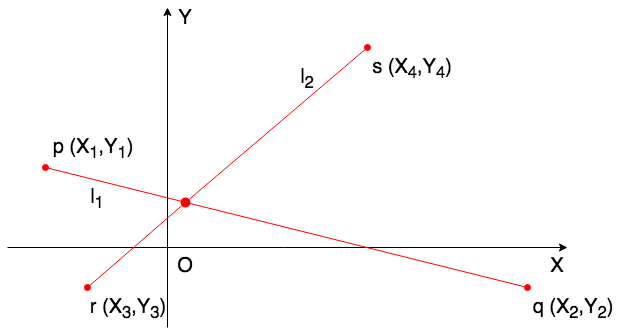
初等數學方法以多項式函數的方式找出交叉點，換句話說，如果找得出交叉點即兩線段交叉。

算法

當p、q皆存在時應符合 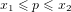與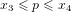

如果p存在但q不存在，有可能會發生以下情形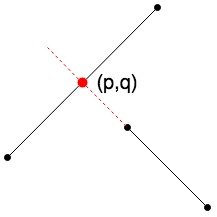

結論

雖然線性函數的方法可以非常容易的以程式碼呈現，但是線性函數使用除法，在程式運行時，可能需要消耗較多時間且浮點數可能使結果不準確。因此，判斷兩線段是否相交，需要進一步分析。

對立與定界框測試 On Opposite Side and Bounding Box Test

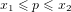導入 與 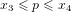的概念，將其細分為兩個測試，對立測試與定界框匡測試。
滿足這兩個測試的兩直線則可能相交。

對立測試

在對立測試中，檢查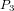 與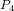 互相在L1的另外一邊。

利用線性函數所推導出的直線方程式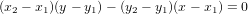
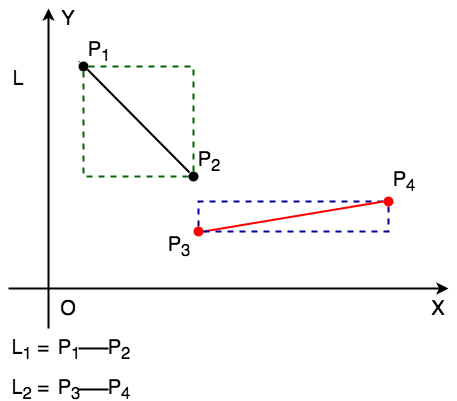
L1 =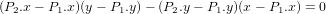
將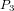 與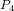 放入左式後，得到g與h值。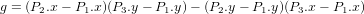


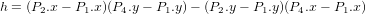
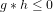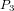如果 成立則 與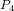 互相在L的另外一邊。

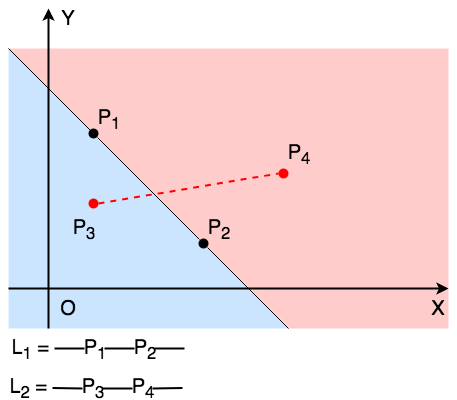
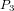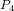雖然對立測試確定了 與 互相在L的另外一邊，但是無法完全說明兩線相交，如下圖：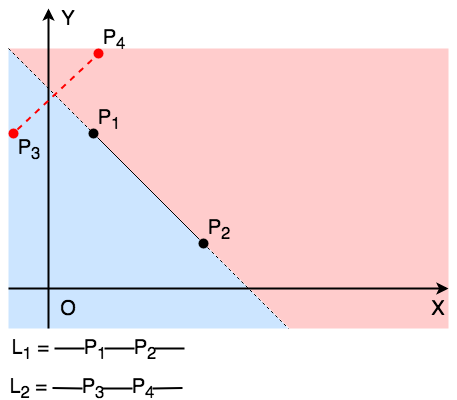

雖然L1與L2相交，卻無法保證兩線相交。

測試二：定界框測試

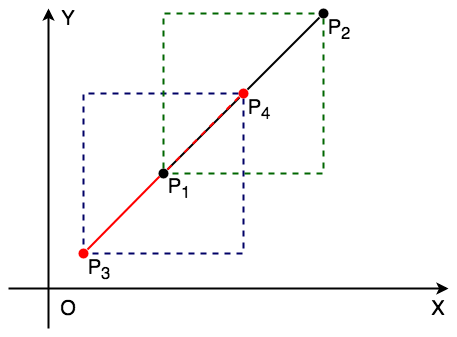
定界框是以線段兩端為矩形斜對角所畫出的矩形框(紅框及藍框)。
而定界框測試為確認兩直線的定界框有重疊部分。
基本上，這個測試會出現三種不同情況。

情況一：定界框重疊且兩線相交

情況二：定界框重疊但兩線不相交

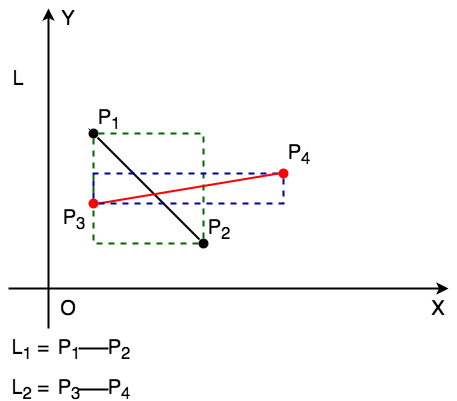
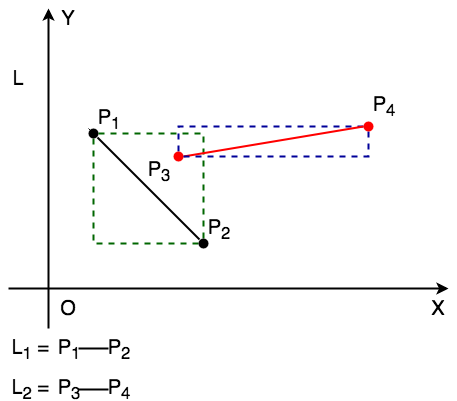
這種情況主要由其中一條直線的兩端點不在另一條直線的兩側，即未通過對立測試。

情況三：定界框不重疊且兩線不相交

這種情況即為未通過定界框測試，且很明顯兩線不可能相交。

缺點

若同時符合兩個情況：

1. L1兩點在L2的兩邊
2. L2兩點在L1的兩邊

這樣已經可以判定大部分情況兩線確實相交，但仍然有漏洞。
如果兩條線平行，則有可能以上情況仍然成立，如圖：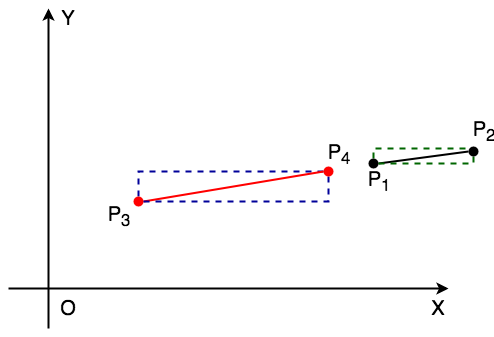

因此，要確定兩線段確實相交，需要以上兩個情況及L1定界框與L2定界框有重疊的情況都成立。