凸包是在n個點中的所圍成的最小凸多邊形。
凸包不需要包含所有的點但是需要將所有的點圍在凸包內。
凸包所圍的多邊形與橡皮筋的概念相似,例如將橡皮筋套在釘板上(紅框),橡皮筋所圍的多邊形與凸包相似。
凸多邊形必須符合以下條件:
簡易的判斷法為,所有的角皆轉向同樣方向(順時鐘或逆時鐘)。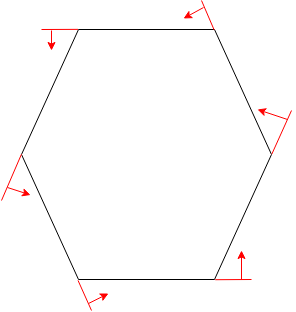
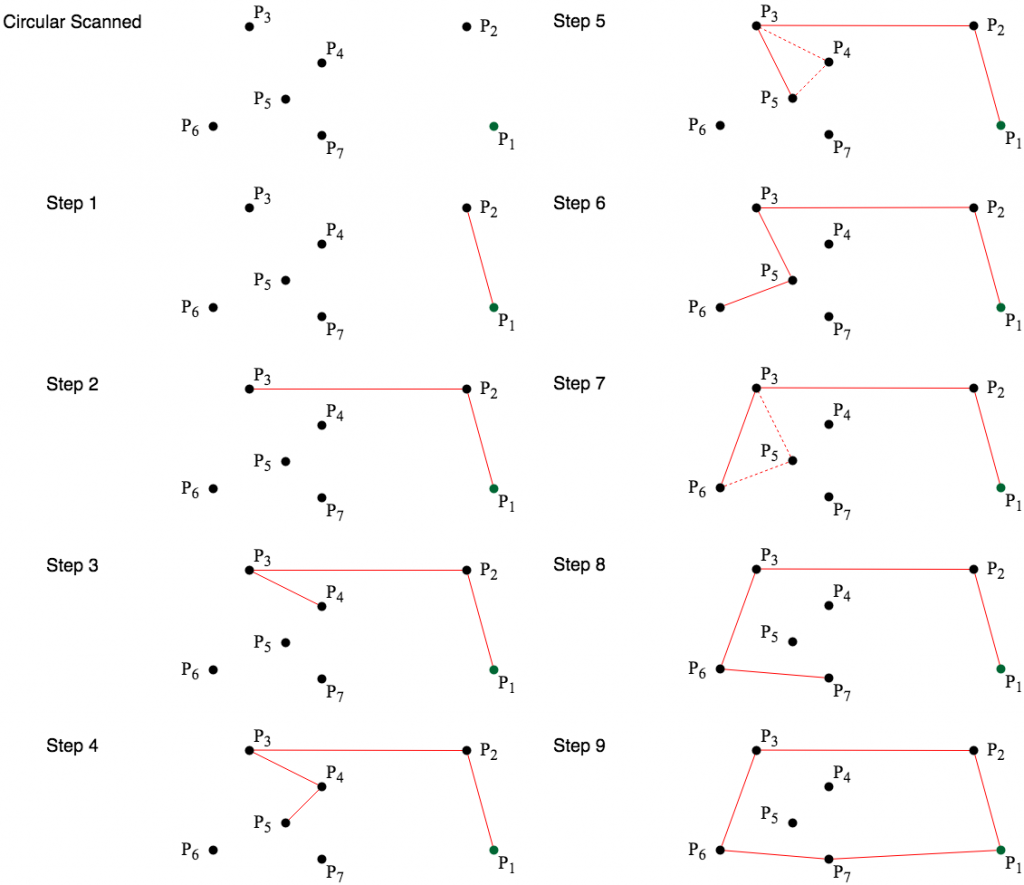
Graham掃描是結合圓型掃描及上述的轉向判斷方法所得到的掃描法。
傳送門:圓型掃描解釋
圓型掃描可以確保所建立的圖形為簡單多邊形。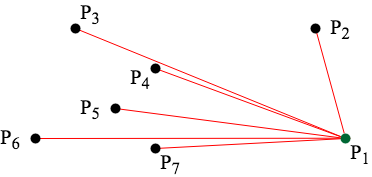
依照圓型掃描後所確認的連接順序開始製圖,同時每連接一個點,都需要確定角度轉向是否一致。
如果連接一點時轉向改變,將開始追朔過去之前所連結的點,並將最後連接的點與上一點連接,直到轉向一致為止。
轉向完全一致且最後一點與第一點後,會建立出一個凸多邊形(凸包)。
如果連接下一點時轉向同方向則繼續連接,直到轉向不同方向或連接至第一點。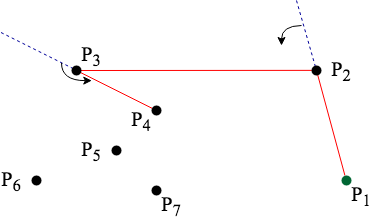
如果連接下一點時轉向不同方向則追朔之前所連接的點。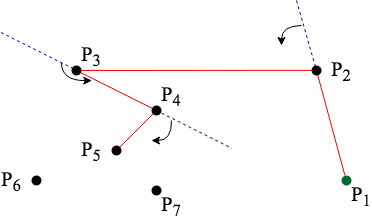
移除上一步驟所連接的線,並且連接最後達到的點與上一階段所達到的點,直到轉向同方向。
當轉向同方向時,繼續連接下一點。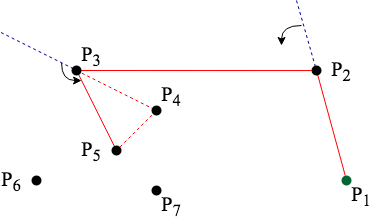
傳送門:[筆記本: 演算法] 多邊形篇 Part 1 - Simple Polygon 簡單多邊形
傳送門:[筆記本: 演算法] 多邊形篇 Part 3 - Furthest Pair of Points 最遠兩點配對
