何謂 八皇后問題

“如何能夠在8×8的西洋棋棋盤上放置八個皇后，任兩個皇后都不能處於同一條橫行、縱行或斜線上。”

假定有一個 safe?的function，來判斷在已經有放置一些皇后的時候，再放置下一個皇后是否安全。
(defn safe? [row col queens-position])。

為什麼叫做"回溯搜索"，舉下面4X4棋盤的例子
嘗試路線：(1,x,x,x)->(1,1,x,x)(不行回到上一步)->(1,x,x,x)->(1,2,x,x)->(1,2,3,x)(有可能全部x位置都不行)，就會回到(1,2,x,x)再繼續下去，歸納"嘗試(成功)->嘗試(成功)->嘗試(失敗，回上一步)"，最後可以得到正確答案。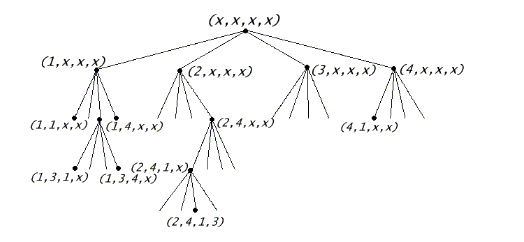

這非常複雜，且這種複雜很難描述，因為太過於注意時序了，先...然後...一步一步前進。

跳脫時間的方法

• 假設已有 k 列前(0 ~ k-1列)的所有解法，要繼續擴充到k列。
• 對k列的每個位置都用safe?做過濾。

(網路上抄的答案 kerker)

(defn safe?
  "Check if queen in last row is safe"
  [positions]
  (let [[queen-pos & left] positions
        k (count positions)
        diags-up (map - left (range 1 (inc k)))
        diags-down (map + left (range 1 (inc k)))]
    (empty? (filter (partial = queen-pos) (concat diags-up diags-down left)))))

(defn queens [board-size]
  ((fn queen-cols [k]
     (if (zero? k)
       (list empty-board)
       (for [rest-of-queens (queen-cols (dec k))
             new-row (range 1 (inc board-size))
             :let [new-cols (cons new-row rest-of-queens)]
             :when (safe? new-cols)]
         new-cols)))
  board-size))

可以看到 for當中的實作：
rest-of-queens -> k列前 所有可行的位置
new-row -> 新列的每一個element
:let ... :when -> 當通過safe?時 執行 (cons new-row rest-of-queens)

結論：
為何會比較容易，因為把所有的解當成一個整體的 "集合"，而不是隨著 "時序的狀態變化" 一個一個地找出的

問題：
流集合的方式確實比較簡單，也容易理解，但是一次直接叫出整個列的element，會不會太耗記憶體，相較於傳統的解法一個一個去分析，雖然時間較長，但比較不耗記憶體。

接下來的 lazy seq 就是要解決太耗記憶體的部分。