黑色好看版 - 傳送門

正文開始

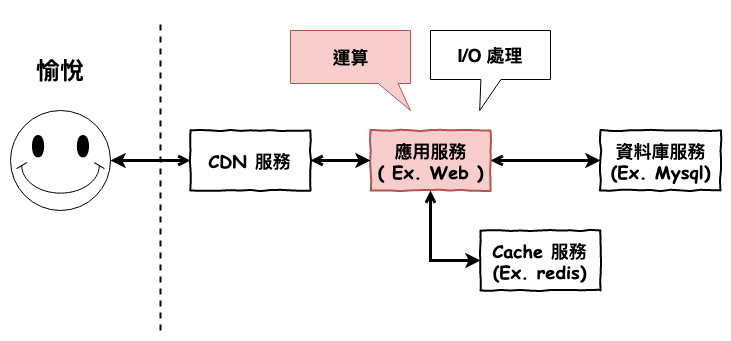
本篇文章開始，我們將要深入的探討，每一個服務，要如何儘可能的達到高性能呢 ?

這首先第一部份，我們要探討以下主題 :

在應用層，要如何儘可能的使用越少的資源( CPU、Memory )，來做最多的事情呢 ?

而這一題的主要的答案就是不少人面試很排斥的『演算法』。

本篇文章會分為以下幾段 :

• 一個好與不好的演算法性能差距多大呢 ?
• 演算法運算時間的分類
• 演算法優化建議

接下來正文開始。

一個好與不好的演算法性能差距多大呢 ?

一個演算法的效能基本上有兩個東東 :

• 時間複雜度: 你可以把它想成演算法的運行時間。
• 空間複雜度: 這個可以想成你這個演算法需要花多少的空間來處理。

上面只是簡單說明它的代表概念，比較實際的運算方法直接去 wiki 看就夠囉。

那麼拉回拉，一個好與不好的演算法性能差距有多大呢 ?

呵 !

我們以一個最簡單的演算法『費波那契數列』來看看。

首先這是好的程式碼。

// good

console.time('time');
function fib (n) {
  if ( n === 0 || n === 1) {
    return n;
  }

  let a = 0;
  let res = 1;
  let temp = 0;

  for (let i=2; i <= n; i++) {
    temp = res;
    res = a + res;
    a = temp;
  }
  return res;
}

fib(45);
console.timeEnd('time');

再來這是爛的程式碼。

// bad

console.time('time');

function fib (n) {
  if ( n === 0 || n === 1) {
    return n;
  }
  return fib(n-1) + fib(n-2);
}

fib(45);
console.timeEnd('time');

然後咱們簡單的測試運行時間，你看看這兩個差多少倍，嗯好幾千倍。

good time: 2.609ms
bad time: 17315.706ms

這裡應該是有些人會想說，這種費波那契數列演算法或是很多演算法上網抓就好了，工作上又不太會自已寫，學演算法要幹啥呢 ?

某些方面是沒錯，但這裡問題在於 :

如果你抓成 bad 版本呢 ? 會發生什麼事情呢 ?

很多演算法的確不需要自已在寫，但如果有演算法概念與能力，至少不太會抓錯程式碼，抓錯這事咱真看過這慘況。

~ 小備註 ~
原本想順到印出 stack 記憶體使用量，但是好像沒啥方法可以印出……。如果不太分的清楚 stack 與 heap 的差別可以參考此篇文章。

How to inspect the memory usage of a process in Node.Js

演算法運算時間的分類

這裡最重要的重點就在於，你要知道你寫的程式碼時間複雜度是屬於那個分級，如果你分不起來，然後寫到 O(2^n) 分級的演算法，那明眼人應該知道會發生什麼事情。

比較常見的分類，分為以下幾種，花費時間由小到大 :

• O ( 1 )
• O ( log n )
• O ( n )
• O ( n log n )
• O ( n ^ 2 )
• O ( 2 ^ n )

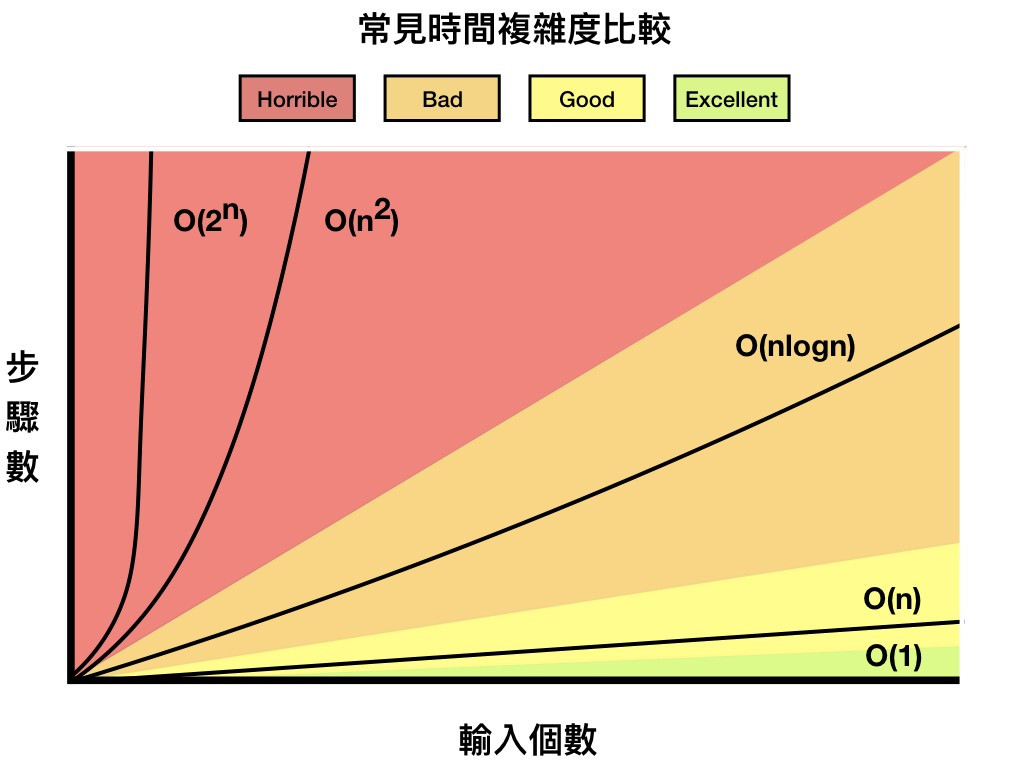
圖 1 : 時間複雜度的分級 (圖片來源: 初學者學演算法｜談什麼是演算法和時間複雜度)

O ( 1 )

例如這種常見的，兩數交換，就是屬於 O(1) 操作。

var a = 1;
var b = 2;

var temp = b;
b = a;
a = temp;

O ( log n )

這個最常見的操作就是所謂的二分搜尋法，簡單的概念如下圖 2 所示，就是一半一半的找，但這個有個前提假設，那就是數組是要有規則或已排序的才能使用這招。

圖 2 : 二分搜尋概念圖

O ( n )

只要有用一個 for 迴圈，那它基本上就屬於 O(n) 的時間複雜度。

for (var i=0; i < n; i++){
   ...
}

O ( n log n )

這裡只要記好，不管是任何的語言，你只要用到它內建的排序功能，那基本上就是 O(nlogn) 的時間複雜度，平均而言喔。

O ( n ^ 2 )

這個也非常的常見，就是內外兩個 for 回圈。

for (var i=0; i < n; i++){
    for (var j=0; j < n; j++){
        ...
    }
}

O ( 2 ^ n )

這種時間複雜度很容易出現在一種情境下，那就是選與不選的情境，不過這種情況比較常在考演算法題時看到，實務應該是不常看到。

實務上 CPU 與 Memory 優化建議

這裡我覺得要讓應用層以最少的 cpu 與 memory 做最多事情的要幾個要點 :

小建議 1 : 可以理解你寫的程式碼的時間與空間複雜度

簡單的說，你要可以知道你寫的程式碼的時間與空間複雜度，不要寫到了 n^5 的迴圈程式都不知道。然後當寫到這種多層迴圈的情況下，你要仔細的想想兩件事 :

• 是否真的有必要 ? 有沒有其它寫法呢 ?
• 如果真的有必要，在多少個數量可能會是臨界點呢 ?

小建議 2 : 熟悉各種工具所提供的方法

例如我們很常使用 redis，它裡面提供了一些資料結構來進行操作，這裡要使用好的要點，就是你要熟悉裡面每個資料結構所提供的操作方法，它的時間複雜度與空間複雜度，這裡如果你選錯了使用方法，那們你可能會耗費不少資源在做事情。

小建議 3 : 熟悉資料結構

現在不少的語言都有提供一些資料結構的操作，但是我相信不少人就是一個陣列幹到底，功能可以出來沒錯，但事實上有些情況下，選擇適當的資料結構使用，你會省下不少力氣並且性能也提升不少。

如果你不知道要學那些資料結構，就乖乖的買本資料結構的書吧。接下來再搭配你會的語言所提供的資料結構，像如果是 c++ 你就可以參考 STL，然後 Java 可以看看 Collection 等，而 js 呢 ? 你就先理解看看它的 Array 到底是啥鬼，並且看看它所提供的方法。

~ 學習小心得 ~

開始或許會覺得很困難，但久了就覺得還好了，畢竟痛久了，就習慣了。

小建議 4 : 熟悉一些演算法的套路

俗話說的好，不要重複做輪子。

多去理解一些演算法，或許會有小收穫，有時後你接到一項工作時，有可能事實上，已有人做過相同的事情了，有的人解決這項任務可能已經有 O(logn) 的寫法，但你偏偏自已寫，然後寫出一個 O(n^2) 的寫法，然後當系統快不行了，就和老闆說只能加機器來處理，這樣有點而不是很好呢

~ 學習小心得 ~

演算法學習也是個很困難的一條路，也同時是很容易讓人放棄的路，但是當你想繼續往上時，演算法就是基本了。建議這一條路找個伴一起學，真的比較不容易放棄，如果最後還是和伴一起放棄了，只能說無緣囉 ~

這裡順到提供一些我的演算法軍火庫，通常在碰到一個問題時，如果沒啥想法就會拿這些方法來思考看看有沒有適合的，而這些方法事實上也可以當成刷題用的分類……

• BFS
• DFS
• Two-Points
• DP
• Binary Search
• Sort
• 資料結構 (tree、set、hash、prefix tree、binary tree)
• BitManipulation
• Recursion
• Divid And Conquer
• Greedy
• 歸納法 (思考方法)
• 演繹法 (思考方法)

請服用。

~ 小知識 ~

歸納法與演繹法這兩種嚴格來說在 leetcode 沒有這種分門別類，但是它卻是所有演算法的核心思考方法。

• 歸納法 : 就是將相同特性的東西歸納出來，例如這個吃漢堡、吃便當，這就可以歸納出吃東西這個概念
• 演繹法 : 就是一種依順序的推導，例如人會死，孔子是人，所以孔子會死。

這裡只是很淺淺的說明，未來有機會希望可以開篇來詳談。

結論與心得

這一篇文章中，咱們討論如何以最少的 CPU 與 Memory 來做最多事情的一個重點，那就是 :

演算法

而且我們也知道，一個好的演算法與爛的算法，運行時間差了幾百倍都有可能，而這個影響在比較大的公司就有可能是百台以上的成本差異，雖然在小公司效果比較不顯著，但是如果寫的爛的話，也有可能少少的使用量下，你的機器就掰了。

然後這裡建議一般的開發者，演算法可以不用刷的要死要活，但至少要有演算法的概念，這樣才對得起付錢給你的人(不過如果你討厭老闆那就無所謂)，但是如果你追求的對是一般，那就乖乖刷吧。

最後簡單的淺淡一下面試演算法這東西。基本上普通的公司，我不太贊成考演算法題目(我說題目喔)。主要的原因有下 :

• 工作時用不到(比較準確的說法是，用了也不見得看得到效果)。
• 有可能會錯失一些在其它方面很強的人。
• 香蕉的問題。

但是我覺得可以簡單的考一些演算法的概念當參考評分比較用，但請不要第一關演算法題目沒過就刷人，除非公司是萬人想進那種類型，或是開得起 $$ 的則例外。

參考資料

• 時間複雜度 講解- 簡單易懂