有的時候，狀態不容易使用表格來表示。又或者，不見得每一個格子都被原本要解的問題依賴。這個時候，就是該使用 Top-Down （遞迴＋記憶化搜索）解法了！記憶化搜索通常會因為存取記憶體的位置不連續，造成其執行速度，在計算相同數量的子問題時，比單純掃過陣列來得慢。但是記憶化搜索的好處有兩個：一是只需要關心遞迴的部份、不需要擔心計算順序，二來只需要計算真正需要計算的狀態，有些狀態不需要去計算它。

對於兩種方法的比較，我覺得這篇 Geeksforgeeks 的文章 寫得不錯，值得參考。

由於 Leetcode 上面我沒有看到什麼好的例子，就憑我的印象跟大家推薦一道經典的程式競賽題目吧！

    如果有看到不錯的 Leetcode 稀疏狀態的動態規劃題目拜託跟我說唷，
    我再把題目加入這篇文章裡面！

Example 17: IOI 2004 - Phidias

題目連結

• IOI 官方網站：https://ioinformatics.org/files/ioi2004problem6.pdf
• Yandex 網站：https://contest.yandex.com/ioi/contest/560/enter/
• PEG Judge：https://wcipeg.com/problem/ioi0421

題目敘述

你有一塊 W x H 大小的板子，你不能把板子隨意轉向。現在你想要從這些板子中切割出一些 W[i] x H[i] 大小的子板子。每一種子板子都是有用的，所以你可以生產 0 個或多個這樣的板子。切割板子是有規範的，每一次你只能選擇水平或垂直方向，一刀切到底並且把板子分成兩半。（也就是說不能像某些國旗那樣切一個角落出來，也不能切割成紙風車的形狀～）

你可以切很多次，最終板子會被分成很多小板子。只要切出來的板子符合任何一種規格，就是有用的板子。如果不符合任何一種規格，我們就定義成被浪費掉的板子。

請問對於任何一種切法，至少得浪費多少面積的板子呢？

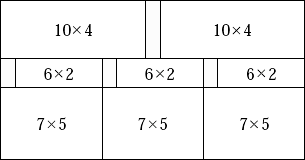
上圖是一個將 21x11 大小的板子切成若干 10x4, 6x2 與 7x5 大小的板子的一種切法，此種切法浪費了共計 10 單位面積的板子。

解題思考

這題動態規劃很好想：拿到 (W, H)，你就隨意切看看，切成 (x, H) 和 (W-x, H) 的垂直組合，或是 (W, y) 和 (W, H-y) 的水平組合。這裡有兩個有趣的觀察：

• 如果目前寬度 W 比起任何一個 W[i] 都來得窄，那顯然整塊都得浪費掉，不需要再切了。（同理也可以推斷 H 那邊的中止條件）
• 此外，對於任何一個 (W, H)，如果 W, H 剛好是某個 W[i], H[i] 的整數倍的話，我們知道一定可以直接把它鋪滿，所以可以直接回傳 0。

這樣時間複雜度是多少呢？W*H*(W+H+N) 看起來大約是 600*600*600，其實有點大呢（尤其是 2004 年那個時候，一秒鐘大概只能跑 10^6 個指令）。但事實上有很多狀態是不會被算到的～因此用 Top-Down 的方法來寫，反而有效率些。

參考程式碼 (C++)

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 205;
const int MAXW = 605;
const int MAXH = 605;
int N;
int w[MAXN], h[MAXN];
int dp[MAXW][MAXH] = {};
bool computed[MAXW][MAXH] = {};

int solve(int W, int H) {
  if (computed[W][H]) return dp[W][H];

  computed[W][H] = true;
  int &ret = dp[W][H];

  // 如果長寬都剛好是某片板子的整數倍的話，就直接回傳啦。
  for (int i = 0; i < N; i++) {
    if (W % w[i] == 0 && H % h[i] == 0)
      return 0;
  }

  // 否則的話就認真切一下板子。
  ret = W * H;
  for (int x = 1; x < W; x++)
    ret = min(ret, solve(x, H) + solve(W-x, H));
  for (int y = 1; y < H; y++)
    ret = min(ret, solve(W, y) + solve(W, H-y));
  return ret;
}

int main() {
  int W, H;
  cin >> W >> H >> N;
  for (int i = 0; i < N; i++) cin >> w[i] >> h[i];
  int ans = solve(W, H);
  cout << ans << endl;
  return 0;
}

後話

IOI (International Olympiad in Informatics，資訊奧林匹亞）是給高中生舉辦的一年一度的程式設計大賽，每一個國家可以派出四名選手，我國近年來表現也都還算不錯呢！2019 年也獲得二金二銅的好成績！由於是辦給高中生的國際賽事，題目品質與水準一向都很不錯，是個值得練習解題思維的好資源～