在上一節中，我們使用參數和超參數將模型定義為數學函數，並介紹了線性模型的參數。然後，我們討論了尋找最佳模型參數集的分析方法。以及如何透過在參數空間中進行搜索來優化參數。但是要將一個點與另一個點進行比較，我們需要採取某種方法。

損失函數

在本節中，我們將討論損失函數，這些函數能夠從訓練集中獲取一組數據點的預測值，並將其組合為一個數字，從而估算模型當前參數的品質。單點預測品質的一種度量標準就是預測值與實際值之間的這種差異。

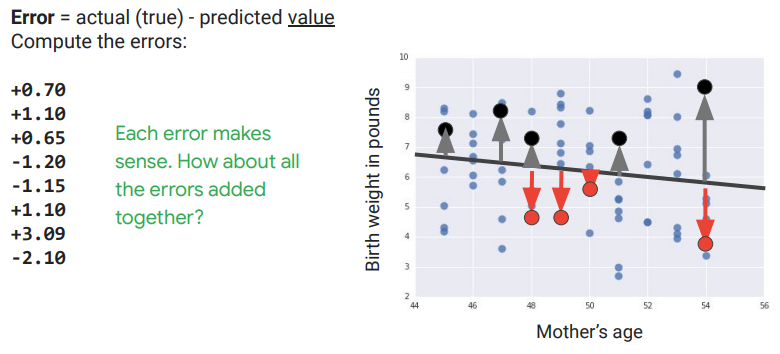
這種差異稱為錯誤(error)。我們如何將一堆錯誤值放在一起？最簡單的方法是將它們組合成一個總和。但是，如果我們使用sum函數來組合我們的誤差項，則結果模型會將相反符號的誤差項視為彼此抵消。儘管我們的模型確實需要處理矛盾的數據，但並不是直接將正負誤差之間的差異進行抵銷。取而代之的是，我們希望為模型保留這樣的錯誤，在該模型中，預測與數據集中所有點的標籤都匹配，而不是對於那些會相互抵消的，帶有符號錯誤的模型。誤差的絕對值之和感覺是一個合理的選擇，但是這種組合數據的方法也存在問題，我們稍後會來處理。這邊通常使用所謂的均方誤差(MSE)是透過從數據集中獲取一組誤差項來計算的。取其平方消除負值，然後計算平方的平均值。

MSE是一個完全有效的損失函數，但存在一個問題。儘管誤差可能以磅、公里或美元為單位，但平方誤差將以磅平方、公里平方或美元平方為單位。這會使MSE難以解釋。因此，我們通常取MSE的平方根(也就是RMSE)作為代替，以獲得我們可以理解的單位。RMSE越大，預測的質量越差。因此，我們要做的是最小化RMSE。