其實本來想放棄這篇的，因為動態規劃實在太博大精深。而且網路上查資料我看完還是黑人問號，不過凡事起頭難，最後還是決定寫最簡單的部分。期望之後變強的我能夠再加補充進來

What's dynamic programming?

「計算並儲存小問題的解，並將這些解組合成大問題的解。」

這邊先記幾個關鍵字 "儲存"、"小問題" 、"組合"、"大問題"。所以基本上一個問題假如能符合以下就可以使用動態規劃來思考

• 可以拆成很多小問題
• 答案可以透過組合小問題來解
• 小問題重覆量很高

雖然動態規劃跟遞迴並不相同，遞迴是函式呼叫函式，而動態規劃一種設計演算法的範型。但他們還是常常被擺在一塊，因為也可以說動態規劃常被拿來優化純遞迴。怎麼說呢?
以上一篇介紹的遞迴著名例子 Fibonacci 來說好了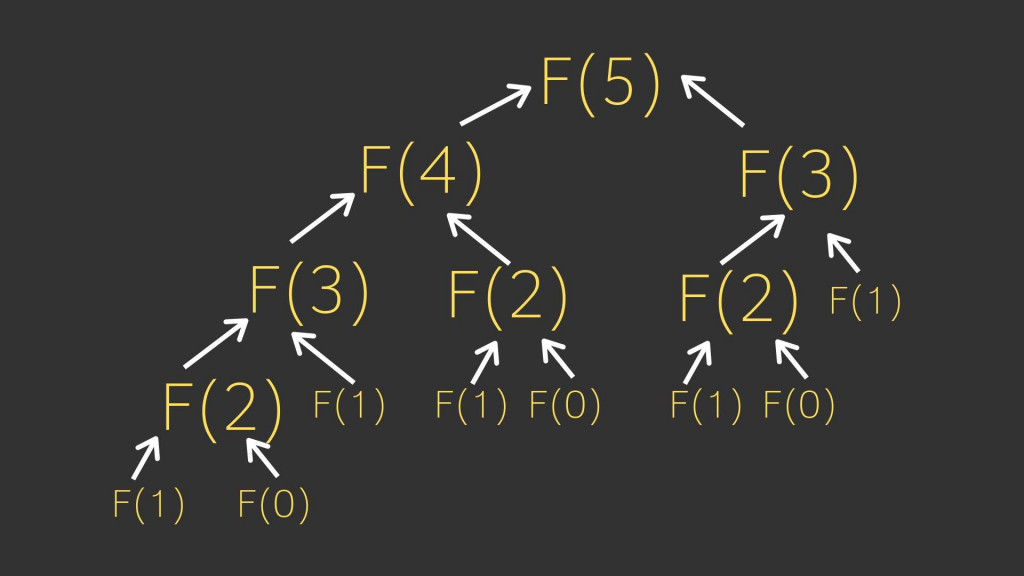

會發現其實 Fibonacci 序列一直再重覆計算一樣的東西，例如 F(1) 被重覆算了 5 次，F(2) 被重覆算了 3 次。
如果我們先"儲存" 這些 "小的值" (減少再次需要被重覆計算)，再 "組合" 成最後 "大結果"，不就可以優化了嗎？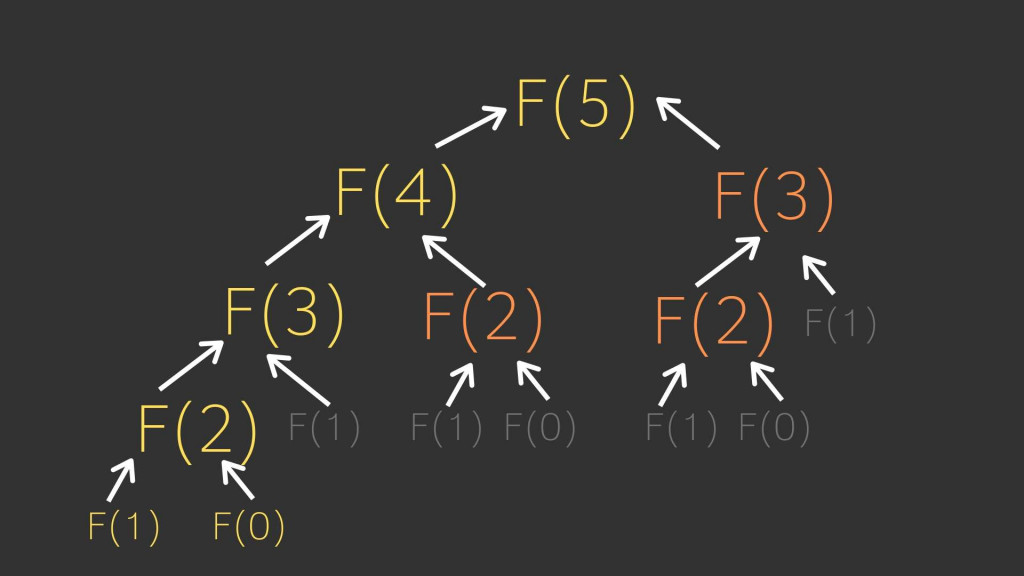

只有黃色部分需要計算，其他都是重覆的不需要再計算一次浪費效能

實際操作

• 檢驗數字是否已經存在 cache 當中
• 如果這個數字已經在 cache 中，則使用這個數字
• 如果這個數字不在 cache 中，把它算出來後放在 cache 中，因此可以在未來被使用

程式碼

let count = 0 // 拿來計算函式執行次數
let yellowCoount = 0; // 拿來計算不在 cache 裡的
function Fibonacci (num, cache = []){
	count ++;
	if(cache[num]){
		return cache[num]
	}else{
		// yellowCoount
		yellowCoount ++;
		if(num == 0){
			cache[num] = 0;
		}else if(num == 1){
			cache[num] = 1;
		}else{
			cache[num] = Fibonacci(num - 1, cache) + Fibonacci(num - 2, cache)
		}
		return cache[num]
	}
	
}
Fibonacci(5); //  
console.log(count) // 9
console.log(yellowCoount) // 6

會發現沒有在 cache 裡的只有黃色部份 6 個，而去存取 cache 裡值有 3 次，所以總共執行 9 次函式，比沒有存 cache 的 15 次少．

觀察 Big O

算每一項的同時我們需要去讀取前兩項的值

• 每次需要 3 個步驟
• 總共需要算 n-1 次,
• 總共的步驟數是 3(n-1) ，拔掉係數後時間複雜度是 O(n)

優化後的 Fibonacci 從 Big O(2^n) 變到 Big O(n)，效能進步超驚人。當 input 越多，就會感受差異更多

n | 正常 F(n) | 優化 F(n)
------------- | -------------
3 | 5 | 5
5 | 15 | 9
7 | 41 | 13
10 | 177 | 19
20 | 21891 | 39

其實我對動態規劃也還在很粗淺的認識階段。連著名的背包問題跟換零錢問題都還沒做過，所以能說的也不太多。有邦友寫動態規劃百題之經典、理論與實作，有興趣可以連去看 ~

參考資料

• 演算法：如何思考動態規劃？
• 用 JavaScript 學習資料結構和演算法：演算法進階補充篇
• [演算法] Fibonacci：善用 cache 和 Memoization 提升程式效能

如有錯誤或需要改進的地方，拜託跟我說。
我會以最快速度修改，感謝您

歡迎追蹤我的部落格，除了技術文也會分享一些在矽谷工作的甘苦。