昨天簡介了一下 Heap 的基本知識
今天就來繼續延伸補足

觀察

1. Heap 常被用來做 Heap sort, priority queue
   • Insertion: O(logn)
   • Delete MAX/min: O(logn)
   • Search MAX/min: O(logn)
   • Build heap: O(n)
2. 降序排列的數組一定是 max heap，但 max heap 不一定是降序排列的數組。
   • T[ ]= {3, 1, 2} 是 max heap 但非降序排列

Fix the Max Heap Property

假設

• 假設 Array A 有 N 個元素
• 而在 root 的左右子樹 A[left(i)] 與 A[right(i)] 都是合法的 max heap
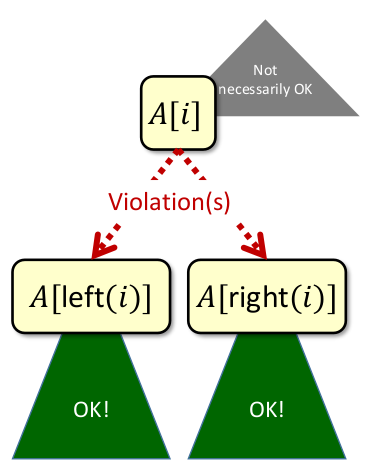
• 但是發生 A[i] < A[left(i)] and/or A i < A[right(i)]

想法

• 假設 A[i] 可能小於任何的 children。
• 通過 swap(A [i], A [left(i)]) 和 swap(A[i], A[right(i)])，可以解決當前小的 heap 中的 Max heap 問題。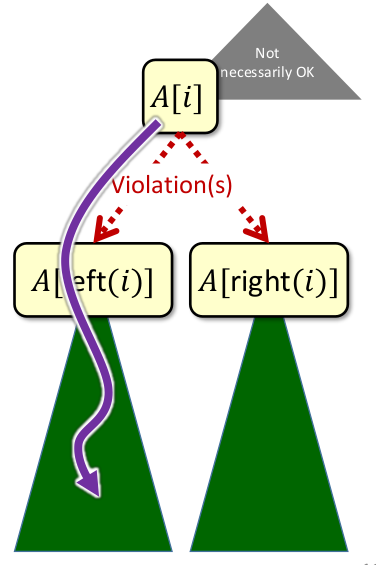
• 假設在原始 A [i] 的新位置又發生違反 max heap 的問題。
• 則在透過遞歸的方式繼續 swap
  

presudo code:

maxHeapify(A, N, i) {
    l = left[i];
    r = right[i];
    if (l < N && A[i] < A[l])
        largest = l;
    else
        largest = i;
    if (r < N && A[largest] < A[r])
        largest = r;
    if (largest ≠ i){
        swap(A[i], A[largest]);
        maxHeapify(A, N, largest);
    }
}