今天來繼續討論各種有趣的 NP 完備問題吧～

漢米爾頓路徑問題 (Hamiltonian Path)

給你一個無向、無權重的圖。請問這個圖是否存在一個經過所有點恰好一次的簡單路徑呢？

（下圖示意為漢米爾頓圈，是指路徑的首尾必須能夠相連的情形。找漢米爾頓路徑和漢米爾頓圈的題目其實是計算上等價的。）

解題思考

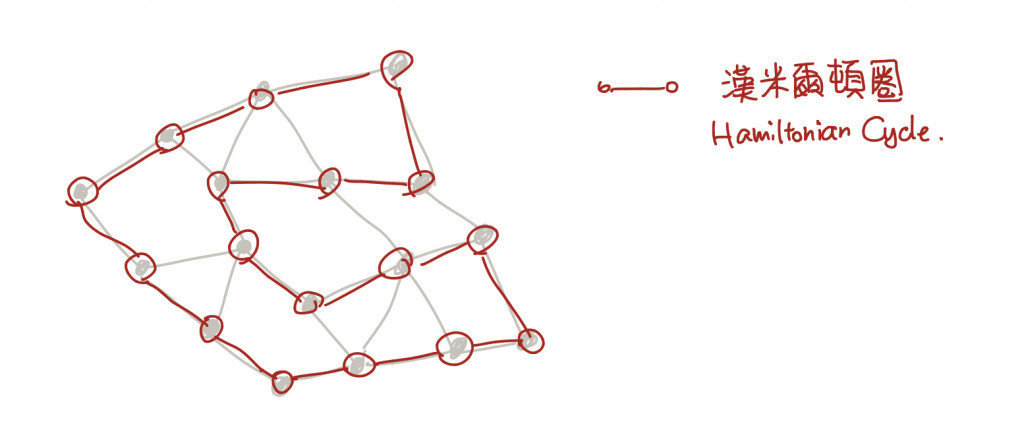
把路徑連接起來、或延伸的時候，我們可以只在乎路徑的端點、不需要在意路徑內部這些點到底是怎麼連起來的。因此這讓我們得到一個稱之為「子集合 DP」的一套動態規劃方法：對於兩個點 s, x 以及一個同時包含 s 和 x 的集合 S 來說，我們可以定義 dp(s, x, S) = 「是否存在一條漢米爾頓路徑從 s 出發、經過所有 S 中的點，然後結束在 x？」要找出遞迴也很簡單：枚舉看看 x 前一個點收在哪裡，然後把 x 從集合中釋放出來就好啦～

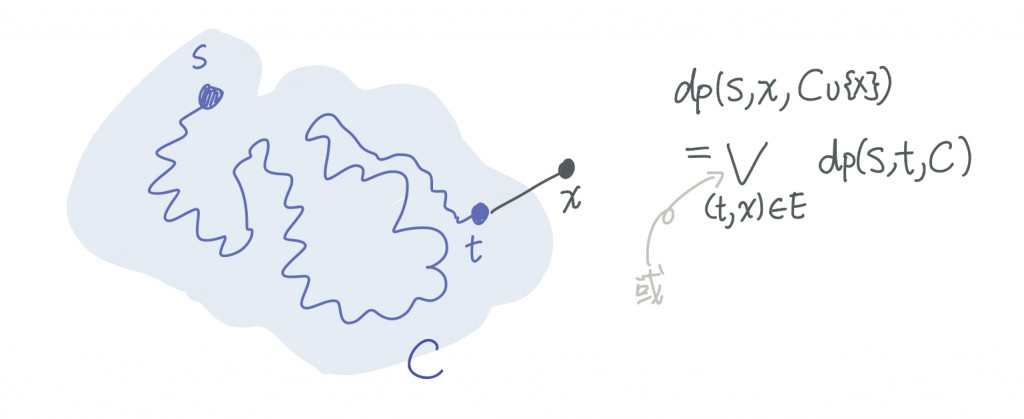
漢米爾頓路徑加上邊的方向與權重以後，就變成了另一個著名的旅行售貨員問題。

旅行售貨員問題 (Traveling Salesperson Problem, TSP)

給你一個有向、有邊權的圖，假設任意兩點之間都存在一條路徑。請找出總長度最短的的一條路徑（或圈）使得每個點經過至少一次。

解題思考

我們可以先找出任兩點之間的最短距離（利用各種最短路徑演算法找出來），然後在圖上加一些「虛擬邊」這些邊的權重就等於兩點之間的最短距離。剩下就可以使用動態規劃一併解決囉！

Exercise 27: Leetcode 943 - Find the Shortest Superstring

題目連結

https://leetcode.com/problems/find-the-shortest-superstring/

題目敘述

給定一些字串，請找出長度最小的字串，使得每一個字串都是它的子字串（連續的那種）。

解題思考

如果我們把所有字串出現在答案字串中的位置，全部標記起來的話，它會是由左而右的一個排列(Permutation)。相反地，隨意給出一個所有字串的排列，欲求出該排列情形下的最短字串，可以拆解成相鄰兩字串的重疊問題——重疊部份越高，接出來的字串越短。

於是，我們可以把整個題目變成一個圖論問題：圖中每一個點 i 是一個字串，從點 i 到點 j 的邊長，則是把字串 A[j] 接在字串 A[i] 後面會增加的最少字元數量。目標就變成要找一個漢米爾頓路徑，使得路徑總長（加上起始字串長度）最小。

參考程式碼 (Python3)

class Solution:
    def shortestSuperstring(self, A: List[str]) -> str:
        n = len(A)
        # 建立兩兩字串之間的「邊長」
        dist = {}
        for i in range(n):
            for j in range(n):
                dist[(i, j)] = min([t for t in range(len(A[j]) + 1) if A[i].endswith(A[j][0:len(A[j])-t])])

        # 因為需要回溯出正確字串，除了 dp 表格以外，還要紀錄是從哪一個字串接過來的
        dp = [[sys.maxsize] * (2**n) for _ in range(n)]
        prev = [[None] * (2**n) for _ in range(n)]

        # 把更新 dp 的函式拉出來另外寫，比較乾淨
        def update(i, state, j):
            val = dp[j][state-(1<<i)] + dist[(j, i)]
            if dp[i][state] > val:
                dp[i][state] = val
                prev[i][state] = j

        # 初始化 dp 表格，考慮一個字串的情形：代價為該字串本身長度        
        for i in range(n):
            dp[i][1<<i] = len(A[i])

        # 對所有狀態來說，我們試圖找出任何一個結尾、然後找出倒數第二個字串把他接上去
        for state in range(0, 2**n):
            for i in range(n):
                if (state&(1<<i)) != 0:
                    for j in range(n):
                        if j != i and (state&(1<<j)) != 0:
                            update(i, state, j)

        # 以下的部份是回溯出原字串
        lengths = [dp[i][(1<<n)-1] for i in range(n)]
        p = [lengths.index(min(lengths))]
        state = (1<<n)-1
        while prev[p[-1]][state] != None:
            x = p[-1]
            p.append(prev[x][state])
            state -= (1<<x)        
        p.reverse()
        ans = A[p[0]]
        for i in range(1, n):
            if dist[(p[i-1], p[i])] > 0:
                ans += A[p[i]][len(A[p[i]])-dist[(p[i-1], p[i])]:]
        return ans

寫起來好長啊...希望之後能找出更乾淨的寫法～