今天來聊聊最長嚴格遞增子序列 (Longest Increasing Subsequence, LIS) 吧！

最長嚴格遞增子序列 (Longest Increasing Subsequence)

給你 N 個數字排成一列，請找出最常的子序列，使得他們按照順序由左而右是嚴格遞增的。比方說輸入的序列是 [3, 6, 2, 4, 9, 5, 7] 那麼當中可以挑出 [2, 4, 5, 7] 是最長的子序列。

解題思考

如果我們很直接地定義 dp(i) 表示「結束在第 i 個元素的嚴格遞增子序列中，最長的長度」，那麼我們可以很輕易地找出它的遞迴關係：

• 用拉的：dp(i) = 1 or max{ dp(j) + 1 | j < i && A[j] < A[i] }
  讓 dp(i) 的值定義為在 i 之前比 A[i] 小的那些位置 j 中，最大的 dp(j) + 1。
• 用推的：dp(k) ← max{ dp(k), dp(i) + 1 } for all k > i && A[k] > A[i]
  取得 dp(i) 的值以後，用它來更新未來所有可能的位置 k，其中 k > i 而且 A[k] > A[i]。

Exercise 29: Leetcode 300 - Longest Increasing Subsequence

題目連結

https://leetcode.com/problems/longest-increasing-subsequence/

題目敘述

給你一個 nums 陣列，輸出 LIS 長度。

參考程式碼 (Python3)

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        dp = [1] * len(nums)
        for i, val in enumerate(nums):
            dp[i] = max([dp[j] + 1 for j in range(0, i) if nums[j] < nums[i]], default=1)
        return max(dp, default=0)

另外一種思考方式

其實 LIS 可以轉換成 LCS：如果我們已經有排序好的數列 A_sort（數值相同時，編號由大至小處理，這樣就不會選到相同數值的資料了，才能夠嚴格遞增），那麼此時便有 LIS(A) = LCS(A, A_sort)。

另一種狀態設計

我們可以考慮另外一種反向思考：定義 lis(i, L) 表示截至 i 為止(A[0..i])，長度為 L 的所有嚴格遞增子序列，結尾最小的數值是多少。不難發現遞迴關係：

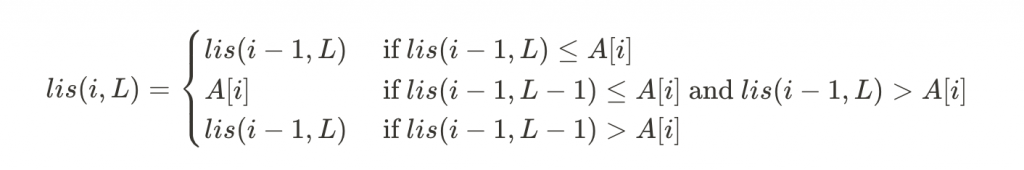
從上面的式子我們可以驚訝地發現，A[i] 只會恰好出現在整排 lis(i, *) 的恰好一個位置！實在是太恰好了，讓我們多恰幾次。恰恰恰恰恰恰恰。每一個新的 i 出現的時候，我們只要用二分搜尋法找出應該把 i 塞進去的位置就好了，其他數字維持不變，如果長度為 L 的序列不存在的話我們就給他無窮大。

第一個正式提出並討論這個想法的人 (應該是 Fredman 或是 Knuth) 其實滿厲害的，我們來看看實作吧！

from bisect import bisect_left

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        lis = []
        for x in nums:
            i = bisect_left(lis, x)
            if i == len(lis):
                lis.append(x)
            else:
                lis[i] = x
        return len(lis)

是不是簡單乾淨俐落呢！

接龍排序法 (Patience Sorting)

這個排序法是從接龍這個概念想出來的：一開始有一疊牌，和一個空盤面。每一次考慮一張牌，如果盤面上有任何一落牌的頂端有數字比手上所持有的牌大的，就放在能放的排堆中，最左邊那一落。否則的話另起爐灶（手上的牌比所有盤面上的最頂上那張都大），把這張牌放到最右邊去。這種擺法能夠確保每次放牌的時候，每一落最頂端的牌都是遞增的（跟 lis 一模一樣）

放完之後，每一疊由頂至底就都會是由小到大排列了，這時候再使用 k-way merge sort 就可以有效率地排列囉！這方法常數可能有點大。所以只有在序列已經差不多排好了的情望下（k很小）做到 O(n log k) 的排序時間。

LIS 還有很多很有趣的相關理論，尤其在組合學的對稱函數 (Symmetric Functions)、楊氏表格 (Young's Table)、RSK 對應 (Robinson-Schensted-Knuth Correspondence) 關係等都有相關且重要的研究，很酷吧！個人最喜歡的是鋪磚塊方法數問題，這個以後我們再談哈哈。